POJ1759 Garland —— 二分
阿新 • • 發佈:2017-09-24
europe p s mon 技術分享 present test time color ima
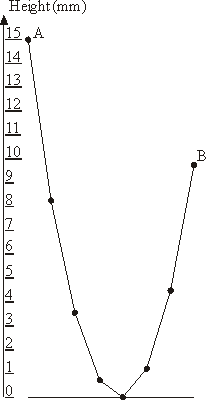 The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.
The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.
The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.
You shall neglect the lamp‘s size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations:
H1 = A
Hi = (Hi-1
HN = B
Hi >= 0, for all 1 <= i <= N
The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75. 
題目鏈接:http://poj.org/problem?id=1759
Garland
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 2477 | Accepted: 1054 |
Description
 The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.
The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps. The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.
You shall neglect the lamp‘s size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations:
H1 = A
Hi = (Hi-1
HN = B
Hi >= 0, for all 1 <= i <= N
The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75.
Input
The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.Output
Sample Input
692 532.81
Sample Output
446113.34
Source
Northeastern Europe 2000 題解: 錯誤思路:慣性思維,一上來就想二分答案,即B點。但問題是,知道了A、B點,怎麽求出中間的點呢?首先遞推是推不出來的,然後就嘗試用遞歸,看能否“先前進再返回”地求出各點,結果還是不行。後來也大概得出結論,如果要求出各個點:1)要麽能推導出關於A、B點的公式直接計算;2)要麽是知道相鄰兩個點的值,然後一路遞推。公式我是推導不出來的,所以就要嘗試第二種方法。所以: 1.二分第二個點,然後一路遞推,直到求出B。 2.根據:H[i] = 2*H[i-1] + 2 - H[i-2] 可知,前兩個點的值越小, 第三個點的值也越小,最終B的值也越小。所以二分的第二個點與B點具有同增同減性。 代碼如下:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 #include <cmath> 7 #include <queue> 8 #include <stack> 9 #include <map> 10 #include <string> 11 #include <set> 12 #define rep(i,a,n) for(int (i) = a; (i)<=(n); (i)++) 13 #define ms(a,b) memset((a),(b),sizeof((a))) 14 using namespace std; 15 typedef long long LL; 16 const double EPS = 1e-8; 17 const int INF = 2e9; 18 const LL LNF = 9e18; 19 const int mod = 1e9+7; 20 const int maxn = 1e5+10; 21 22 int n; 23 double A, ans; 24 25 bool test(double x1, double x2) 26 { 27 for(int i = 3; i<=n; i++) //遞推出每個點的高度 28 { 29 double x3 = 2*x2+2-x1; 30 if(x3<=0) return false; //出現負數,證明接地了, 不符合。 31 x1 = x2, x2 = x3; 32 } 33 ans = x2; //符合條件, 則更新答案。 34 return true; 35 } 36 37 int main() 38 { 39 while(scanf("%d%lf", &n, &A)!=EOF) 40 { 41 double l = 0, r = A; //二分第二個點 42 while(l+EPS<=r) 43 { 44 double mid = (l+r)/2; 45 if(test(A, mid)) 46 r = mid - EPS; 47 else 48 l = mid + EPS; 49 } 50 printf("%.2f\n", ans); 51 } 52 }View Code
POJ1759 Garland —— 二分

