無監督學習
無監督學習
監督學習通過發現數據的其他屬性和類別屬性之間的關聯模式並通過對這些模型來預測未知數據實例的類別屬性。這些屬性通常表示一些現實世界中的預測或分類問題,例如通過判斷新聞是屬於體育類還是屬於政治類,而在其他的應用中,數據的類別屬性卻是缺失的。用戶希望通過瀏覽數據來發現其中的某些內在結構。例如聚類是一種發現這種內在結構的技術。聚類把全體數據實例組織成一些相似組,這些相似組被稱為聚類。處於相同聚類中的數據實例彼此相似,處於不同聚類中的實例則彼此不同。聚類技術經常被稱為無監督學習。因為與監督學習不同,在聚類中數據類別的分類或分組信息是沒有的。
1 k-均值算法
給定一個數據點集合和需要的聚類數目K,K-均值算法根據某個距離函數反復地把數據分入k個聚類中。
K-均值聚類的算法實現
Algorithm k-means(k,D)
選擇K個點作為初始質心
Repeat
將每個點指派到最近的質心,形成K個簇
重新計算每個簇的質心
Until 質心不再發生變化
?
先選取K個數據點作為聚類中心,再計算每個數據點與各個中心的劇烈,把每個數據點分配給距離它最近的聚類中心。聚類中心以及分配給它的數據點就代表一個聚類。一旦全部數據點被分配了,每個聚類中心會根據該聚類中現有的數據點被重新計算。這個過程將不斷重復直到某個結束條件。
結束條件分為以下:
- 沒有數據點被重新分配給不同的聚類
- 沒有聚類中心再發生變化
- 誤差平方和局部最小
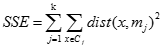
其中k表示需要的聚類數目,
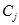 表示第j個聚類,
表示第j個聚類,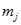 是聚類的聚類中心,
是聚類的聚類中心,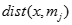 表示數據點和聚類中心之間的距離。
表示數據點和聚類中心之間的距離。
在那些均值能被定義和計算的數據集上的均值均使用k-均值算法。在歐式空間中,聚類的均值(中心)可以用下式計算:
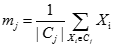
其中
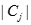 表示
表示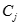 中數據點的個數,例如,3個二維點(1,1)、(2,3)和(6,2)的中心就是((1+2+6)/3,(1+3+2)/3)=(3,2)
中數據點的個數,例如,3個二維點(1,1)、(2,3)和(6,2)的中心就是((1+2+6)/3,(1+3+2)/3)=(3,2)
?
數據點和聚類均值(中心)之間的距離可以被計算如下:
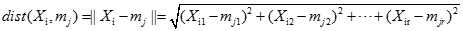
2 二分k均值算法
二分K均值算法是k均值算法的改進版,她基於一個簡單的思想:為了得到k個簇,將所有點的集合分類成兩個簇,從這些簇中選取一個繼續分類,如此下去,直到產生k個簇。
二分K均值算法的實現
Algorithm Bit k-means(k,D)
初始化簇表,使之包含由所有的點組成的簇
Repeat
從簇中取出一個簇
{對選定的簇進行多次二分"實驗"}
For i=1 to 實驗次數 do
使用基本k均值,二分選定的簇
Endfor
從二分實驗中選擇具有最小SSE的兩個簇
將這兩個簇添加到簇表中
Until 簇中包含k個簇
3 優點和缺點
優點:K均值簡單並且可以用於多種數據類型。
缺點:
(1)該算法要求用戶隨機選擇初始質心,使得K均值算法受初始化影響較大。
????(2)改算法不太適合處理非球形簇、不同尺寸的簇、不同密度的簇,同時對於離群點的簇進行分類時,也有缺陷。
?
?
?
?
?
?
?
?
?
參考文獻:
[1] http://blog.csdn.net/xuelabizp/article/details/51872462
[2] http://blog.csdn.net/zouxy09/article/details/17590137
無監督學習
