http://poj.org/problem?id=3693

題意：
給定一個字符串，求重復次數最多的連續重復子串。

思路：

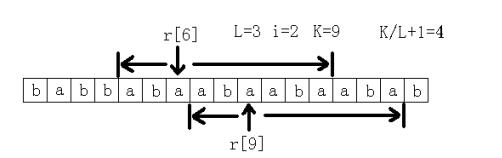
這道題確實是搞了很久，首先枚舉連續子串的長度L，那麽子串肯定包含了r[k]，r[k+2*L]，r[k+3*L].....（k是某個數）中相鄰的兩個。現在我們只需要枚舉這相鄰的兩個，求出它們的最長公共前綴M，那麽重復次數就是M/L+1。

由於要求的是字典序最小，最後再用sa數組從最前面的子串去找即可，符合條件的第一個即是答案。

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<cstring>
  4
 
 #include<cstdio>
  5 #include<vector>
  6 #include<stack>
  7 #include<queue>
  8 #include<cmath>
  9 #include<map>
 10 #include<set>
 11 using namespace std;
 12 typedef long long ll;
 13 typedef pair<int,int> pll;
 14 const int INF = 0x3f3f3f3f
 
;
 15 const int maxn=200000+5;
 16 
 17 int n;
 18 char s[maxn];
 19 int sa[maxn],t[maxn],t2[maxn],c[maxn];
 20 int Rank[maxn],height[maxn];
 21 int d[maxn][30];
 22 int ans[maxn];
 23 
 24 void build_sa(int m)
 25 {
 26     int *x=t,*y=t2;
 27     //基數排序
 28     for(int i=0;i<m;i++)    c[i]=0
 
;
 29     for(int i=0;i<n;i++)    c[x[i]=s[i]]++;
 30     for(int i=1;i<m;i++)    c[i]+=c[i-1];
 31     for(int i=n-1;i>=0;i--) sa[--c[x[i]]]=i;
 32     for(int k=1;k<=n;k<<=1)
 33     {
 34         int p=0;
 35         //直接利用sa數組排序第二關鍵字
 36         for(int i=n-k;i<n;i++)  y[p++]=i;
 37         for(int i=0;i<n;i++)    if(sa[i]>=k)    y[p++]=sa[i]-k;
 38         //基數排序第一關鍵字
 39         for(int i=0;i<m;i++)    c[i]=0;
 40         for(int i=0;i<n;i++)    c[x[y[i]]]++;
 41         for(int i=1;i<m;i++)    c[i]+=c[i-1];
 42         for(int i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
 43         //根據sa和y計算新的x數組
 44         swap(x,y);
 45         p=1;
 46         x[sa[0]]=0;
 47         for(int i=1;i<n;i++)
 48             x[sa[i]]=y[sa[i-1]]==y[sa[i]]&&y[sa[i-1]+k]==y[sa[i]+k]?p-1:p++;
 49         if(p>=n)
 50             break;
 51         m=p;                //下次基數排序的最大值
 52     }
 53 }
 54 
 55 void getHeight(int n)
 56 {
 57     int i,j,k=0;
 58     for(i=1;i<=n;i++)  Rank[sa[i]]=i;
 59     for(i=0;i<n;i++)
 60     {
 61         if(k)  k--;
 62         int j=sa[Rank[i]-1];
 63         while(s[i+k]==s[j+k])  k++;
 64         height[Rank[i]]=k;
 65     }
 66 }
 67 
 68 void RMQ(int n)
 69 {
 70     for(int i=1;i<=n;i++)  d[i-1][0]=height[i];
 71     for(int j=1;(1<<j)<=n;j++)
 72         for(int i=0;i+(1<<j)-1<n;i++)
 73         d[i][j]=min(d[i][j-1],d[i+(1<<(j-1))][j-1]);
 74 }
 75 
 76 int query(int L, int R)
 77 {
 78     int k=0;
 79     while((1<<(k+1))<=R-L+1)  k++;
 80     return min(d[L][k],d[R-(1<<k)+1][k]);
 81 }
 82 
 83 int LCP(int a, int b)
 84 {
 85     int x=Rank[a],y=Rank[b];
 86     if(x>y)  swap(x,y);
 87     x--; y--;
 88     if(y<0)  return 0;
 89     return query(x+1,y);
 90 }
 91 
 92 void solve(int n)
 93 {
 94     int MAX=-1;
 95     int len = 0;
 96     for(int l=1;l<n;l++)   //枚舉子串長度
 97     {
 98         for(int i=0;i+l<n;i+=l)  //枚舉起點
 99         {
100             int k=LCP(i,i+l);
101             int m=k/l+1;
102             int t=l-k%l;  //如果不是l的倍數，則往前幾位再匹配，往後匹配已經匹配不上了
103             t=i-t;
104             if(t>=0 && k%l)
105             {
106                 if(LCP(t,t+l)>=k)  m++;
107             }
108             if(m>MAX)
109             {
110                 len=0;
111                 ans[len++]=l;
112                 MAX=m;
113             }
114             else if(m==MAX)
115                 ans[len++]=l;
116         }
117     }
118     int l, start;  //尋找字典序最下的答案
119     bool flag=false;
120     for(int i=1;i<=n;i++)
121     {
122         if(flag)  break;
123         for(int j=0;j<len;j++)
124         {
125             int tmp=ans[j];
126             if(LCP(sa[i],sa[i]+tmp)>=(MAX-1)*tmp)
127             {
128                 start=sa[i];
129                 l=tmp*MAX;
130                 flag=true;
131                 break;
132             }
133         }
134     }
135     for(int i=start;i<start+l;i++)
136         printf("%c",s[i]);
137 
138     printf("\n");
139 }
140 
141 int main()
142 {
143     //freopen("in.txt","r",stdin);
144     int kase=0;
145     while(~scanf("%s",s))
146     {
147         if(s[0]==‘#‘)  break;
148         memset(Rank,0,sizeof(Rank));
149         printf("Case %d: ",++kase);
150         n=strlen(s);
151         if(n==1)  {printf("%c\n",s[0]);continue;}
152         s[n]=‘0‘;
153         n++;
154         build_sa(128);
155         getHeight(n-1);
156         RMQ(n-1);
157         solve(n-1);
158     }
159     return 0;
160 }

POJ 3693 Maximum repetition substring（連續重復子串）