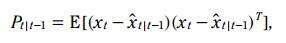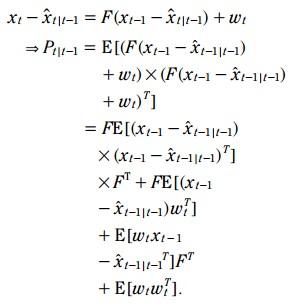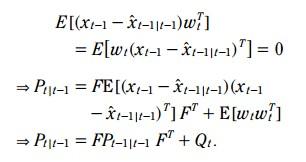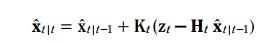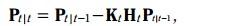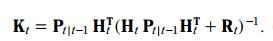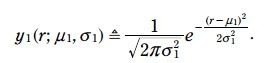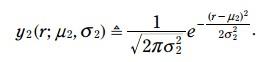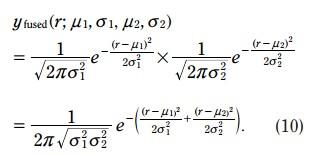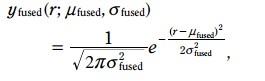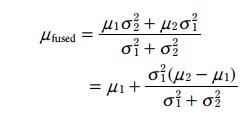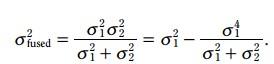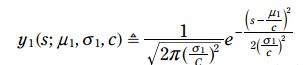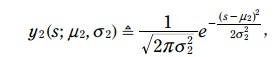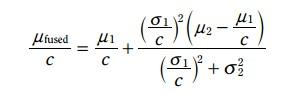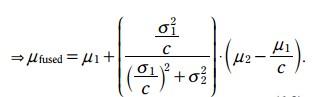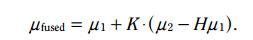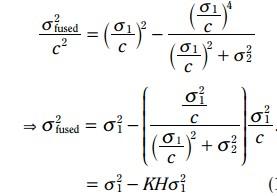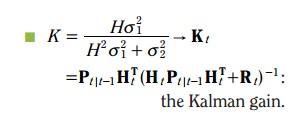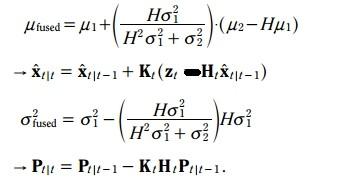[Math]理解卡爾曼濾波器 (Understanding Kalman Filter)
1. 卡爾曼濾波器介紹
卡爾曼濾波器的介紹, 見 Wiki
這篇文章主要是翻譯了 Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation
感謝原作者。
如果敘述有誤,歡迎指正!
2. 基本模型
2.1 系統模型
卡爾曼濾波模型假設k時刻的真實狀態是從(k − 1)時刻的狀態演化而來,符合下式:
 (1)
(1)
- Fk 是作用在 Xk−1 上的狀態變換模型(/矩陣/矢量)。
- Bk 是作用在控制器向量uk上的輸入-控制模型。
- Wk 是過程噪聲,並假定其符合均值為零,協方差矩陣為Qk的多元正態分布。
 (2)
(2)
2.2 測量模型
時刻k,對真實狀態 xk的一個測量zk滿足下式:
 (3)
(3)
其中Hk是觀測模型,它把真實狀態空間映射成觀測空間,vk 是觀測噪聲,其均值為零,協方差矩陣為Rk,且服從正態分布。
 (4)
(4)
初始狀態以及每一時刻的噪聲{x0, w1, ..., wk, v1 ... vk} 都認為是互相獨立的.
卡爾曼濾波要做的是:
已知:
-
系統的初始狀態 x0
-
每個時間的測量 Z
-
系統模型和測量模型
求解:
狀態x隨著時間變化而產生的值
3. 預測與更新
3.1 預測方程
預測是這樣一個問題:
已知:
- 上一個狀態的更新值
- 上一個狀態的更新值和真實值之間的誤差
求解:
- 這一個狀態的預測值
- 這一個狀態的預測值和真實值之間的誤差
過程包括兩個方面:
一、由上一個更新值 Xk-1|k-1 預測這一個預測值 Xk|k-1
二、由上一個更新值和真實值之間的誤差 Pk-1|k-1 預測下一個預測值和真實值之間的誤差 Pk|k-1
具體來說,就是以下兩個方程。
 (預測狀態) (5)
(預測狀態) (5)
 (預測估計協方差矩陣) (6)
(預測估計協方差矩陣) (6)
這裏:
Xk-1|k-1 這種記法代表的是上一次的更新值,後面一個 k-1可以看做 Zk-1, 也就是上一次經過對比Zk-1(實際就是更新)之後所估計出的狀態Xk-1。
Xk|k-1 這種記法代表這一次的預測值, 同理於剛才的介紹, 經過上一次Zk-1之後所估計出的狀態Xk。
預測公式-預測狀態
也就是公式(5), 可以直接由系統模型導出。
預測公式-協方差矩陣:
P代表著估計誤差的協方差,代表著一種 confidence ,比如先驗估計誤差(預測值與真實值之間誤差)的協方差
註:
方差有兩種形式
協方差的定義:
如果說方差是用來衡量一個樣本中,樣本值的偏離程度的話。協方差就是用來衡量兩個樣本之間的相關性有多少,也就是一個樣本的值的偏離程度,會對另外一個樣本的值偏離產生多大的影響,協方差是可以用來計算相關系數的,相關系數P=Cov(a.b)/Sa*Sb, Cov(a.b)是協方差, Sa Sb 分別是樣本標準差。【可以參考另一篇博客《理解協方差》】
cov(x,y)
= E( (x-u)(y-v)‘ )
= E(xy‘ - xv‘ - uy‘ + uv‘)
= E(xy‘) - E(xv‘) - E(uy‘) + E(uv‘)
= E(xy‘) - uv‘ - uv‘ + uv‘
= E(xy‘) - uv‘
比較(5)和(1), 相減:
由於 狀態估計誤差 和 系統噪聲 是不相關的
註:
如果隨機變量 x和y是不相關的, 那麽
Cov(x,y) = 0
=> E( (x-ex)(y-ey)‘ ) = 0
=> E(xy‘) - ex*ey‘ = 0
如果 ex 和ey為0 => E(x,y‘) = 0 就像上面的情況, 誤差和噪聲都服從正態分布,所以期望都是0 .
獨立的充要條件:P(xy) = P(x)P(y)
3.2 更新方程
更新過程實際上就是一下問題:
已知:
- 由上一個更新值得到的當前的預測值。
- 當前的觀測值
- 觀測模型
求解:
- 融合了預測值和觀測的更新值
- 由預測值的估計誤差得到更新值的估計誤差
更新方程如下:
其中K稱為kalman增益, 就像一個補償,決定著預測值應該變化多少幅度,才能變成更新值。
先看一個簡單的例子,從這個例子中來推導出這三個方程。
3.3 簡單的例子
3.3.1 舉例
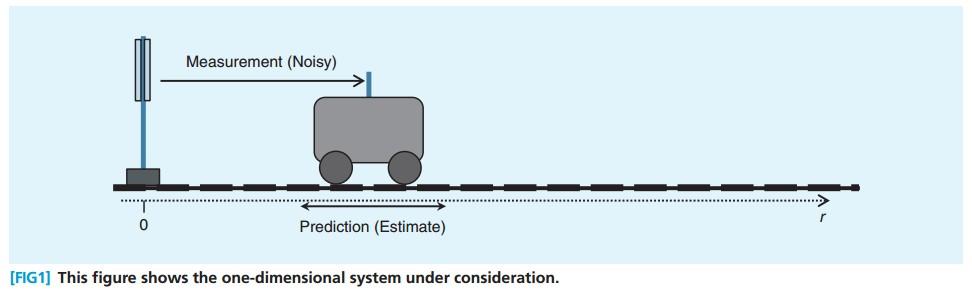
有一個直線軌道, 軌道上有一個火車,從火車站出發, 在t時刻,火車想要知道自己距離火車站的位置,可以有兩個信息來源:
- 根據 t-1時刻的狀態信息,以及一些控制信息來推斷, 狀態包括 t-1時刻的位置、速度等, 控制信息包括司機剎車、加速等等。
- 根據 t時刻的測量數據來推斷, 這裏假設車上有一個聲波發射器,可以探測到發射到火車站需要多少時間,進而得到離車站的距離。
要想得到一個比較好的結果,顯然不能只依靠某一種方法來推斷,而 Kalman Filter的方法是:
-
首先, 利用t-1時刻進行推斷, 這一步叫預測。
-
然後, 利用t時刻的measurement 也可以推斷, 使用這個推斷對預測進行校正, 這一步叫更新。
3.3.2 火車位置 - 預測
t=0的時候, 火車狀態如 Figure.2 ,這時候, 火車的位置是比較準確的。
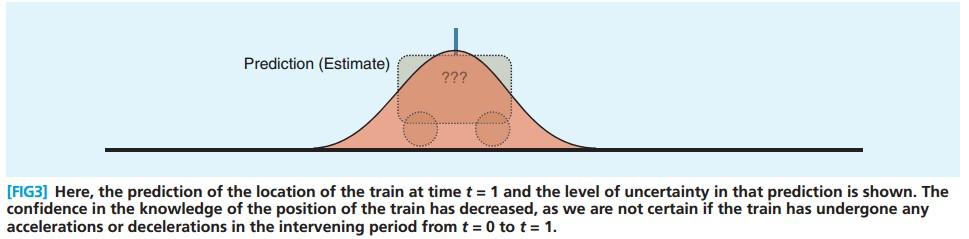
t=1的時候, 火車的預測狀態如 Figure.3 可以看到, 位置的方差變大了。
火車的預測主要遵循 式(1),而預測的方差在不斷變大,也就是說預測的準確度在下降, 這是由累積誤差 w 導致的。
3.3.3 火車位置 - 測量
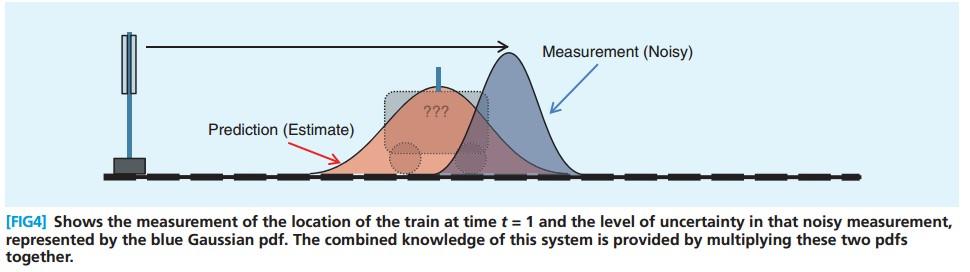
t=1 的時候,我們還有 measurement ,同樣可以推斷火車的位置,見下圖中的藍色的pdf
3.3.4 火車位置 - 更新
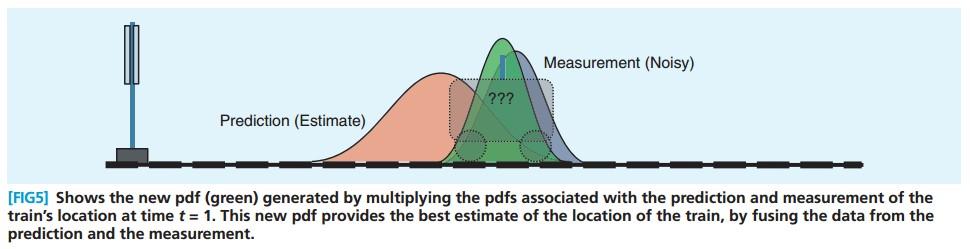
將兩個pdf相乘,得到下圖中的綠色pdf, 綠色pdf中較高的位置, 意味著預測和測量對這個位置都比較支持。
這裏有一個高斯分布的一個重要性質就是,兩個高斯分布的乘積還是高斯分布。
This is critical as it permits an endless number of Gaussian pdfs to be multiplied over time, but the resulting
function does not increase in complexity or number of terms; after each
time epoch the new pdf is fully represented by a Gaussian function. This
is the key to the elegant recursive properties of the Kalman filter。
3.3.5 推導更新方程
紅色的pdf是預測的火車位置, 方程如下:
藍色的pdf是測量的火車位置, 方程如下:
綠色的pdf二者融合的或者位置, 方程如下:
寫成如下形式:
這裏:
這兩個式子,就是kalman濾波的更新方程
但是,這只是一個很特殊的例子,因為這裏假設預測和測量都是采用同樣的坐標系
更現實的情況是二者需要統一到一個 domain 中
比如上面所舉的例子中:
預測的時候, 預測值是用米作為單位的。
但是當測量的時候, 測量得到的值是用聲波經過的秒數作為單位的。
必須先要把兩個量統一到同一個domain才能進行融合。
比如上式子中, y2 (measurement)實際是聲波傳遞時間的一個正態分布,也就是說單位是秒。
一般做法是把
預測值 => 測量值
y1就變成:
y2不變:
這樣兩個坐標系都在 mesaurement domain 了。
兩個pdf所在坐標系的橫軸都是表示時間,而且以秒為單位了。
`
統一domain之後,更新方程就有了如下形式
3.3.5.1 期望更新方程:
將
H = 1/c
K = 
這裏的H就相當於觀測方程中的H, K就是卡爾曼增益。
3.3.5.2 方差更新方程:
類似地, 融合之後的方差更新變成了
4. 總結
各個變量對應的情況如下:
最終的更新方程
5. 實現
Talk is cheap, show me the code.
%本例子從百度文庫中得到, 稍加註釋
clear
N=200;%取200個數
%% 生成噪聲數據 計算噪聲方差
w=randn(1,N); %產生一個1×N的行向量,第一個數為0,w為過程噪聲(其和後邊的v在卡爾曼理論裏均為高斯白噪聲)
w(1)=0;
Q=var(w); % R、Q分別為過程噪聲和測量噪聲的協方差(此方程的狀態只有一維,方差與協方差相同)
v=randn(1,N);%測量噪聲
R=var(v);
%% 計算真實狀態
x_true(1)=0;%狀態x_true初始值
A=1;%a為狀態轉移陣,此程序簡單起見取1
for k=2:N
x_true(k)=A*x_true(k-1)+w(k-1); %系統狀態方程,k時刻的狀態等於k-1時刻狀態乘以狀態轉移陣加噪聲(此處忽略了系統的控制量)
end
%% 由真實狀態得到測量數據, 測量數據才是能被用來計算的數據, 其他都是不可見的
H=0.2;
z=H*x_true+v;%量測方差,c為量測矩陣,同a簡化取為一個數
%% 開始 預測-更新過程
% x_predict: 預測過程得到的x
% x_update:更新過程得到的x
% P_predict:預測過程得到的P
% P_update:更新過程得到的P
%初始化誤差 和 初始位置
x_update(1)=x_true(1);%s(1)表示為初始最優化估計
P_update(1)=0;%初始最優化估計協方差
for t=2:N
%-----1. 預測-----
%-----1.1 預測狀態-----
x_predict(t) = A*x_update(t-1); %沒有控制變量
%-----1.2 預測誤差協方差-----
P_predict(t)=A*P_update(t-1)*A‘+Q;%p1為一步估計的協方差,此式從t-1時刻最優化估計s的協方差得到t-1時刻到t時刻一步估計的協方差
%-----2. 更新-----
%-----2.1 計算卡爾曼增益-----
K(t)=H*P_predict(t) / (H*P_predict(t)*H‘+R);%b為卡爾曼增益,其意義表示為狀態誤差的協方差與量測誤差的協方差之比(個人見解)
%-----2.2 更新狀態-----
x_update(t)=x_predict(t) + K(t) * (z(t)-H*x_predict(t));%Y(t)-a*c*s(t-1)稱之為新息,是觀測值與一步估計得到的觀測值之差,此式由上一時刻狀態的最優化估計s(t-1)得到當前時刻的最優化估計s(t)
%-----2.3 更新誤差協方差-----
P_update(t)=P_predict(t) - H*K(t)*P_predict(t);%此式由一步估計的協方差得到此時刻最優化估計的協方差
end
%% plot
%作圖,紅色為卡爾曼濾波,綠色為量測,藍色為狀態
%kalman濾波的作用就是 由綠色的波形得到紅色的波形, 使之盡量接近藍色的真實狀態。
t=1:N;
plot(t,x_update,‘r‘,t,z,‘g‘,t,x_true,‘b‘);
6. Reference
Wiki-卡爾曼濾波器
Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation
Wiki-協方差矩陣
[Math]理解卡爾曼濾波器 (Understanding Kalman Filter)