— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they‘ve never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of a, b and c distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 1. For any two islands of the same colour, either they shouldn‘t be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they‘d also like to test your courage. And you‘re here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998 244 353. Two ways are considered different if a pair of islands exist, such that there‘s a bridge between them in one of them, but not in the other.

The first and only line of input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 5 000) — the number of islands in the red, blue and purple clusters, respectively.

Output one line containing an integer — the number of different ways to build bridges, modulo 998 244 353.

1 1 1

8

1 2 2

63

1 3 5

3264

6 2 9

813023575

In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 23 = 8.

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

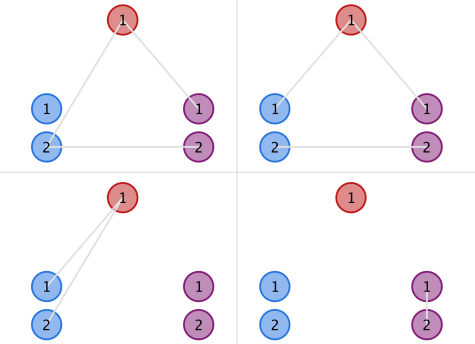
　　題目大意 有3個群島，每個群島中有一些互不相同的島嶼，現在建一些橋，使得同一群島內的兩個島嶼要麽不連通要麽最短路至少經過3條橋。給定三個群島包含的島數，求合法的建橋的方案數。

　　顯然有某個群島中的某個島只能連接其他群島中的一個島。群島與群島之間的建橋互相獨立，所以考慮分開計算。

　　考慮兩個群島之間建立k座橋，那麽方案數就是

　　所以對於兩個群島之間的建橋方案數for一遍就求完了，最後把答案乘起來就行了。

Code

 1 /**
 2  * Codeforces
 3  * Problem#869C
 4  * Accepted
 5  * Time: 30ms
 6  * Memory: 0k
 7  */ 
 8 #include <bits/stdc++.h>
 9 #ifndef WIN32
10 #define Auto "%lld"
11 #else
12 #define Auto "%I64d"
13 #endif
14 using namespace std;
15 
16 #define ll long long
17 
18 void exgcd(ll a, ll b, ll& d, ll &x, ll &y) {
19     if(!b)    {
20         d = a, x = 1, y = 0;
21     } else {
22         exgcd(b, a % b, d, y, x);
23         y -= (a / b) * x; 
24     }
25 }
26 
27 ll inv(ll a, ll n) {
28     ll d, x, y;
29     exgcd(a, n, d, x, y);
30     return (x < 0) ? (x + n) : (x);
31 }
32 
33 const int moder = 998244353;
34 int a, b, c;
35 
36 inline void init() {
37     scanf("%d%d%d", &a, &b, &c); 
38 }
39 
40 long long calc(int x, int y) {
41     long long rt = 1;
42     long long Px = 1, Py = 1;
43     for(int i = 1; i <= x && i <= y; i++) {
44         Px = (Px * (x - i + 1) % moder) * inv(i, moder) % moder;
45         Py = (Py * (y - i + 1)) % moder;
46         rt = (rt + (Px * Py % moder)) % moder;
47     }
48     return rt;
49 }
50 
51 inline void solve() {
52     long long ra = calc(a, b);
53     long long rb = calc(b, c);
54     long long rc = calc(c, a);
55     long long res = ((ra * rb) % moder) * rc % moder;
56     printf(Auto, res);
57 }
58 
59 int main() {
60     init();
61     solve();
62     return 0;
63 }

Codeforces Round #439 (Div. 2) Problem C (Codeforces 869C) - 組合數學