今天，還是國慶和中秋雙節的時間節點，一個天氣不錯的日子，孩子已經早早的睡覺了，玩了一整天，也不睡覺，累的實在扛不住了，勉強洗澡結束，倒床即睡著的節奏。。。

不多說題外話，進入正題。

什麽是A*搜索算法呢？就用百科的解說吧：

A*算法，A*（A-Star)算法是一種靜態路網中求解最短路徑最有效的直接搜索方法，也是解決許多搜索問題的有效算法。算法中的距離估算值與實際值越接近，最終搜索速度越快。

A*搜索的實際應用場景很多，但是大家最為熟悉的恐怕莫過於遊戲了。典型的遊戲就是穿越障礙尋寶，要求在最少的代價內找到寶貝，通常遊戲中的代價，就是用最少的步驟實現寶貝的找尋。還有一種遊戲場景是，給定入口地點，用最少的步驟走到指定的出口地點，中間有障礙物，每次只能在上下左右四個方向上走一步，且不能穿越障礙物。

就拿第二種遊戲場景來解釋A* search具體指的是什麽內容吧。

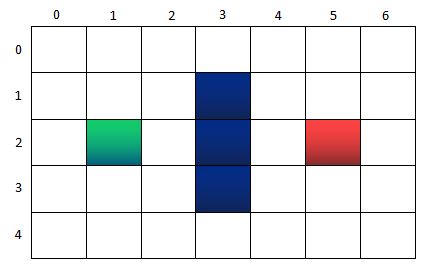
如上圖所示，假設我們有一個7*5的迷宮方格，綠色的點表示起點，紅色的點表示終點。中間三個藍色的格子表示一堵墻，是障礙物。遊戲的規則，是綠色的起點，每次只能向上下左右4個方向中移動一步，且不能穿越中間的墻，以最少的步驟到達紅色的終點。

在解決這個問題之前，先要引入A*搜索算法的核心集合和公式：

核心集合：OpenList，CloseList

核心公式：F=G+H

其中，OpenList和CloseList用來存儲格子點信息，OpenList表示可到達格子節點集合，CloseList表示已到達格子節點集合。

F=G+H表示對格子價值的評估，G表示從起點到當前點的代價；H表示從當前點到達終點的代價，指不考慮障礙物遮擋的情況下，這裏，代價是指走的步數。至於F，就是對G和H的綜合評估了，當然F越小，則從起點到達終點付出的代價就越小了。

就實際操作一下吧。還是上面的圖，每個節點，用n(x,y)表示,x表示橫坐標，y表示縱坐標，比如綠色的起點是n(1,2)：

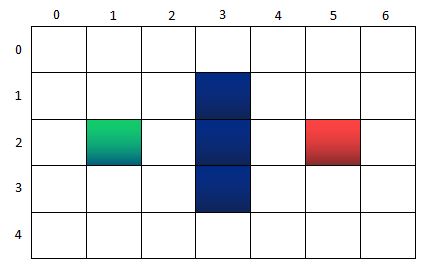
第一步：把起點放入OpenList裏面。

OpenList： n(1,2)

CloseList

第二步：找出OpenList中F值最小的方格，即唯一的方格n(1,2)作為當前方格，並把當前格移出OpenList，放入CloseList。表示這個格子已到達且驗證過了。

OpenList

CloseList：n(1,2)

第三步：找出當前格上下左右所有可到達的格子，看它們是否在OpenList當中。如果不在，加入OpenList，計算出相應的G、H、F值，並把當前格子作為它們的“父節點”。

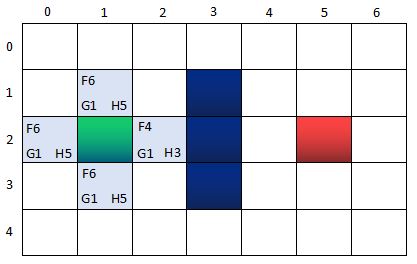
OpenList：n(0,2), n(1,1), n(2,2), n(1,3)

CloseList：n(1,2)

其中，n(0,2), n(1,1), n(2,2), n(1,3)的父節點是n(1,2).所謂的父節點，表示當前的這幾個節點n(0,2), n(1,1), n(2,2), n(1,3)都是從這個所謂的父節點出發得到的分支節點，父節點用作後續找出最短路徑用的。

上述3步，是一次局部尋路的過程，我們需要不斷的重復第二步第三步，最終找到到達終點的最短路徑。

第二輪 ~ 第一步：找出OpenList中F值最小的方格，即方格n(2,2)作為當前方格，並把當前格移出OpenList，放入CloseList。代表這個格子已到達並檢查過了。

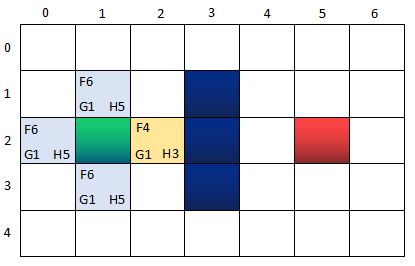
此時的兩個核心集合的節點信息：

OpenList：n(0,2), n(1,1), n(1,3)

CloseList：n(1,2), n(2,2)

其中，n(0,2), n(1,1), n(1,3)的父節點是n(1,2)，n(2,2)的上一級節點（也可以稱為父節點）是n(1,2).

第二輪 ~ 第二步：找出當前格上下左右所有可到達的格子，看它們是否在OpenList當中。如果不在，加入OpenList，計算出相應的G、H、F值，並把當前格子作為它們的“父節點”。

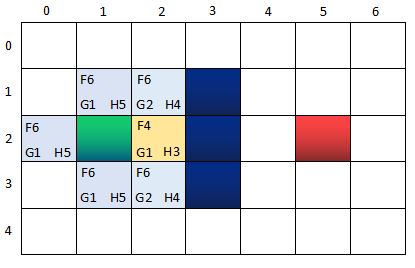
此時的兩個核心集合的節點信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1), n(2,3)

CloseList：n(1,2) <-----n(2,2)

其中，n(0,2), n(1,1), n(1,3)的父節點是n(1,2)，而n(2,1), n(2,3)的父節點是n(2,2). CloseList中節點的指向關系，反映了尋路的路徑過程。

為什麽這一次OpenList只增加了兩個新格子呢？因為n(3,2)是墻壁，自然不用考慮，而n(1,2)在CloseList當中，說明已經檢查過了，也不用考慮。

第三輪 ~ 第一步：找出OpenList中F值最小的方格。由於這時候多個方格的F值相等，任意選擇一個即可，比如n(2,3)作為當前方格，並把當前格移出OpenList，放入CloseList。代表這個格子已到達並檢查過了。

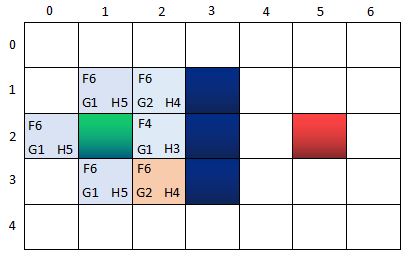
此時的兩個核心集合的節點信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1)

CloseList：n(1,2) <-----n(2,2)<-----n(2,3)

其中，n(0,2), n(1,1), n(1,3)的父節點是n(1,2)，而n(2,1)的父節點是n(2,2)。CloseList中節點的指向關系，反映了尋路的路徑過程。

第三輪 ~ 第二步：找出當前格上下左右所有可到達的格子，看它們是否在OpenList當中。如果不在，加入OpenList，計算出相應的G、H、F值，並把當前格子作為它們的“父節點”。

此時的兩個核心集合的節點信息：

OpenList：n(0,2), n(1,1), n(1,3)；n(2,1) ；n(2,4)

CloseList：n(1,2) <-----n(2,2)<-----n(2,3)

其中，n(0,2), n(1,1), n(1,3)的父節點是n(1,2)，而n(2,1)的父節點是n(2,2)。n(2,4)的父節點是n(2,3). CloseList中節點的指向關系，反映了尋路的路徑過程。

剩下的就是以前面的方式繼續叠代，直到OpenList中出現終點方格為止。

實際的推理，就到這裏，下面，將結合上述的推理理論，用java程序，加以實現。今天，先將偽代碼附上，改天將具體的java實現代碼貼上來。

public Node AStarSearch(Node start, Node end) {
    // 把起點加入openList  
    openList.add(start);
    //主循環，每一輪檢查一個當前方格節點
    while (openList.size() > 0) {
        // 在OpenList中查找F值最小的節點作為當前方格節點
        Node current = findMinNode();
        // 當前方格節點從open list中移除
        openList.remove(current);
        // 當前方格節點進入closeList
        closeList.add(current);
        // 找到所有鄰近節點
        List<Node> neighbors = findNeighbors(current);
        for (Node node : neighbors) {
            if (!openList.contains(node)) {
                //鄰近節點不在openList中，標記父親、G、H、F，並放入openList
                markAndInvolve(current, end, node);
            }
        }
        //如果終點在OpenList中，直接返回終點格子
        if (find(openList, end) != null) {
            return find(openList, end);
        }
    }
    //OpenList用盡，仍然找不到終點，說明終點不可到達，返回空
    return null;
}

JAVA代碼實現待續。。。

A* search算法