監督學習中關於線性回歸問題的系統討論
轉自穆晨
閱讀目錄
- 前言
- 基本線性回歸解決方案 - 最小二乘法
- 最小二乘法的具體實現
- 局部加權線性回歸
- 嶺回歸
- 具體方案的制定
- 小結
前言
本文將系統的介紹機器學習中監督學習的回歸部分,系統的講解如何利用回歸理論知識來預測出一個分類的連續值。
顯然,與監督學習中的分類部分相比,它有很鮮明的特點:輸出為連續值,而不僅僅是標稱類型的分類結果。
回到頂部基本線性回歸解決方案 - 最小二乘法
“給出一堆散點,求出其回歸方程。" -> 對於這個問題,很多領域都碰到過,而其中最為經典普遍的做法通常是:
1. 用式子表示出各個散點到回歸線之間的距離之和:

m 為散點數量,yi 為散點值,xi 為散點坐標,w 為回歸系數向量。
2. 對上式以向量 w 求導,求出導數值為 0 時的回歸系數 (具體求導過程涉及到對向量求導的相關法則,略):

這種方法就叫做最小二乘法。
回到頂部最小二乘法的具體實現
下面這個小程序從文本中讀取散點,然後擬合出回歸直線,並使用 matplotlib 展示出來 (註: 為了清楚直觀,特征 0 沒展示出來):

1 #!/usr/bin/env python 2 # -*- coding:UTF-8 -*- 3 4 ‘‘‘ 5 Created on 20**-**-** 6 7 @author: fangmeng 8 ‘‘‘ 9 10 from numpy import * 11 12 def loadDataSet(fileName): 13 ‘載入測試數據‘ 14 15 numFeat = len(open(fileName).readline().split(‘\t‘)) - 1 16 dataMat = []; labelMat = [] 17 fr = open(fileName) 18 for line in fr.readlines(): 19 lineArr =[] 20 curLine = line.strip().split(‘\t‘) 21 for i in range(numFeat): 22 lineArr.append(float(curLine[i])) 23 dataMat.append(lineArr) 24 labelMat.append(float(curLine[-1])) 25 return dataMat,labelMat 26 27 #=================================== 28 # 輸入: 29 # xArr: 特征坐標矩陣 30 # yArr: 特征值矩陣 31 # 輸出: 32 # w: 回歸系數向量 33 #=================================== 34 def standRegres(xArr,yArr): 35 ‘采用最小二乘法求擬合系數‘ 36 37 xMat = mat(xArr); 38 yMat = mat(yArr).T 39 xTx = xMat.T*xMat 40 if linalg.det(xTx) == 0.0: 41 print "該矩陣無法求逆" 42 return 43 ws = xTx.I * (xMat.T*yMat) 44 return ws 45 46 def test(): 47 ‘展示結果‘ 48 49 # 采用最小二乘求出回歸系數並預測出各特征點對應的特征值 50 xArr, yArr = loadDataSet(‘/home/fangmeng/ex0.txt‘) 51 ws = standRegres(xArr, yArr) 52 xMat = mat(xArr) 53 yMat = mat(yArr) 54 yHat = xMat * ws 55 56 import matplotlib.pyplot as plt 57 58 # 繪制所有樣本點 59 fig = plt.figure() 60 ax = fig.add_subplot(111) 61 ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:, 0].flatten().A[0]) 62 63 # 繪制回歸線 64 xCopy = xMat.copy() 65 xCopy.sort(0) 66 yHat = xCopy*ws 67 ax.plot(xCopy[:, 1], yHat) 68 plt.show() 69 70 if __name__ == ‘__main__‘: 71 test()

測試結果:

觀察預測與真實的相關系數:
1 print corrcoef(yHat.T, yMat)
測試結果:

0.98+的相關系數,可見擬合的效果還是不錯的。
回到頂部局部加權線性回歸
基本的線性回歸經常會碰到一些問題。
比如由於線性回歸本身導致的欠擬合問題。以最基本的一個特征的情況為例,如果散點圖本身呈現一個非線性化的輪廓,而強行的將它擬合成一條直線:

顯然,兩端的擬合是非常不科學的,偏離的很遠。
針對這個問題,局部加權線性回歸應運而生。它能夠得到類似下圖這樣更為科學的擬合線段:

所謂局部,就是最大程度考慮待預測點附近的點,所謂加權,就是離待預測點越近,其參考系數(權重)就越大。
因此,在原先的最小二乘法中加入一個用於衡量權重的對角矩陣W。這樣,回歸系數的求解式就變為:

權重矩陣W又稱為 "核",典型的高斯核的計算方法如下:

下面是采用局部加權線性回歸思想的回歸系數求解函數:

1 #=================================== 2 # 輸入: 3 # testPoint: 測試點 4 # xArr: 特征坐標矩陣 5 # yArr: 特征值矩陣 6 # k: 高斯核權重衰減系數 7 # 輸出: 8 # testPoint * ws: 測試點集對應的結果 9 #=================================== 10 def lwlr(testPoint,xArr,yArr,k=1.0): 11 ‘對指定點進行局部加權線性回歸‘ 12 13 xMat = mat(xArr); 14 yMat = mat(yArr).T 15 m = shape(xMat)[0] 16 17 # 采用向量方式計算高斯核 18 weights = mat(eye((m))) 19 for j in range(m): 20 diffMat = testPoint - xMat[j,:] 21 weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) 22 23 xTx = xMat.T * (weights * xMat) 24 if linalg.det(xTx) == 0.0: 25 print "錯誤: 系數矩陣無法求逆" 26 return 27 28 ws = xTx.I * (xMat.T * (weights * yMat)) 29 return testPoint * ws 30 31 #=================================== 32 # 輸入: 33 # testArr: 測試點集 34 # xArr: 特征坐標矩陣 35 # yArr: 特征值矩陣 36 # 輸出: 37 # yHat: 測試點集對應的結果集 38 #=================================== 39 def lwlrTest(testArr,xArr,yArr,k=1.0): 40 ‘對指定點集進行局部加權回歸‘ 41 42 m = shape(testArr)[0] 43 yHat = zeros(m) 44 45 # 求出所有測試點集的 46 for i in range(m): 47 yHat[i] = lwlr(testArr[i],xArr,yArr,k) 48 return yHat

如下代碼展示回歸結果:

1 def test(): 2 ‘展示結果‘ 3 4 # 載入數據 5 xArr, yArr = loadDataSet(‘/home/fangmeng/ex0.txt‘) 6 7 # 獲取所有樣本點的局部加權回歸的預測值 8 yHat = lwlrTest(xArr, xArr, yArr, 0.01) 9 10 xMat = mat(xArr) 11 srtInd = xMat[:,1].argsort(0) 12 xSort = xMat[srtInd][:,0,:] 13 #print xMat[srtInd][:,0,:] 14 15 # 顯示所有樣本點和局部加權擬合線段 16 import matplotlib.pyplot as plt 17 fig = plt.figure() 18 ax = fig.add_subplot(111) 19 ax.plot(xSort[:,1], yHat[srtInd]) 20 ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0], s=2, c=‘red‘) 21 plt.show()

當k(衰減系數) = 1時,測試結果:

k(衰減系數) = 0.003時,測試結果:

k(衰減系數) = 0.01時,測試結果:

觀察可以發現,k = 1就是和基本線性回歸一樣了 - 欠擬合;而 k = 0.003 則是過擬合了;k = 0.01 剛好,是最優的選擇。
回到頂部嶺回歸
假如碰到了這樣的情況:散點個數小於特征數了。
這種情況有啥問題呢 ---- (xTx)-1 必然會求解失敗!解決辦法可以采用嶺回歸技術。
所謂嶺回歸,就是在回歸系數求解式中的 xTx 之後加上 λI 使求逆部分可順利求解,更改後的求解式如下:

其中,I 是單位對角矩陣,看起來有點像山嶺。這也是為什麽這種回歸方式叫做嶺回歸,哈哈!
具體的實現代碼本文就不具體給出了,但是有兩個地方要特別註意一下:
1. 需要對所有的數據進行標準化
2. 根據不同的 λ 取到不同組的回歸系數之後,還需要對不同組的權重進行擇優。比較常用的有 lasso 方法(和嶺回歸的區別在於 w 和 λ 的約束關系)。
回到頂部具體方案的制定
提到了這麽多種的回歸方案,那麽具體應該采用哪種好呢?
首先,得根據問題的特性選擇合適的方案。然後,使用同一組測試集測試每組方案的相關系數情況。
另外,實踐表明在同樣適用的情況下,"偏差與方差折中" 是一條很重要的經驗法則。

紅點位置對應的方案便是最佳方案。
另外,關於偏差和方差的區別,可參考下圖:
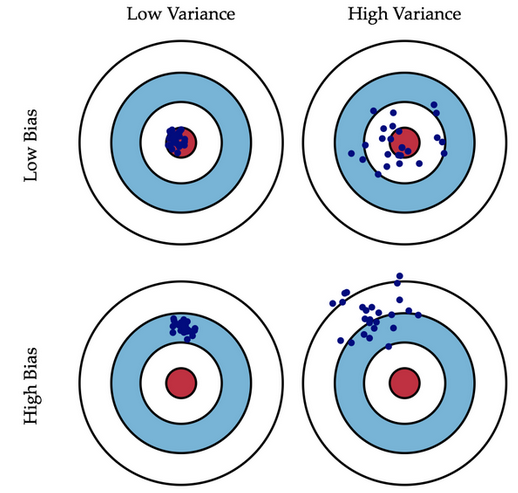
回到頂部
小結
回歸和分類一樣,針對不同問題不同領域都有著不同算法。關鍵是要把握其整體思路,根據需要去進行選擇。
然而,本文所講解的都是線性回歸。線性回歸始終有其弊端,因為很多實際問題本身是非線性的。
因此在下篇文章中,將會專門詳細地介紹一種高級的非線性回歸法 - 樹回歸。
監督學習中關於線性回歸問題的系統討論
