學習筆記 | 回歸模型 | 01 介紹
阿新 • • 發佈:2017-10-09
ren 筆記 reg 影響 stand 他在 sid res parent 01 Introduction
Regression toward the mean 趨均數回歸
弗朗西斯·高爾頓
他在論及遺傳對個體差異的影響時,首次提到了相關系數的概念。比如他研究了“居間親”和其成年子女的身高關系,發現居間親和其子女的身高有正相關,即父母的身材較高,其子女的身材也有較高的趨勢。反之,父母的身材較低,其子女也有較矮的趨勢。同時發現子女的身高常與其父母略有差別,而呈現“回中”趨勢,即回到一般人身高的平均數。
R函數 ‘Jitter’ (Add Noise) to Numbers
Description 描述
Add a small amount of noise to a numeric vector.
對一個數字向量加上一些噪音(小數點後幾位的數字)
Usage
jitter(x, factor = 1, amount = NULL)
Arguments
x numeric vector to which jitter should be added.
factor numeric.
amount numeric; if positive, used as amount (see below), otherwise, if = 0 the default is factor * z/50.
Default (NULL): factor * d/5 where d is about the smallest difference between x values.
Examples
round(jitter(c(rep(1, 3), rep(1.2, 4), rep(3, 3))), 3)
## These two ‘fail‘ with S-plus 3.x:
jitter(rep(0, 7))
jitter(rep(10000, 5))
應用:在畫圖時,通過制造微小的誤差,可以把原本同一值上的點顯示出來,才能在圖上直接看出數據點的“密度”
> summary(regrline) Call: lm(formula = child ~ parent, data = galton) Residuals: Min 1Q Median 3Q Max -7.8050 -1.3661 0.0487 1.6339 5.9264 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 23.94153 2.81088 8.517 <2e-16 *** parent 0.64629 0.04114 15.711 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.239 on 926 degrees of freedom Multiple R-squared: 0.2105, Adjusted R-squared: 0.2096 F-statistic: 246.8 on 1 and 926 DF, p-value: < 2.2e-16 直線的斜率 = 這條回歸線summary中的 parent ~ Estimate 的值 = 0.64629 斜率的標準差 = summary 中的 parent ~ Std.Error 的值 = 0.04114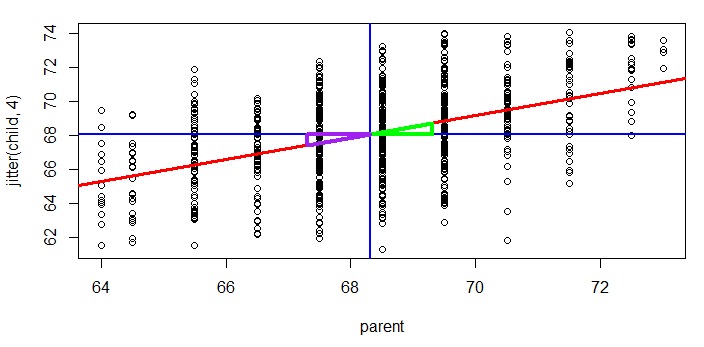
![技術分享]() 如圖,縱軸藍色線為 child 的均值,橫軸藍色線為 parent 的均值。
兩條藍色線的相交點剛好在回歸線上。
向右父母身高 + 1,則子孫身高 + 0.65
同理,向左父母身高 - 1, 則子孫身高 - 0.65
如圖,縱軸藍色線為 child 的均值,橫軸藍色線為 parent 的均值。
兩條藍色線的相交點剛好在回歸線上。
向右父母身高 + 1,則子孫身高 + 0.65
同理,向左父母身高 - 1, 則子孫身高 - 0.65
> summary(regrline) Call: lm(formula = child ~ parent, data = galton) Residuals: Min 1Q Median 3Q Max -7.8050 -1.3661 0.0487 1.6339 5.9264 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 23.94153 2.81088 8.517 <2e-16 *** parent 0.64629 0.04114 15.711 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.239 on 926 degrees of freedom Multiple R-squared: 0.2105, Adjusted R-squared: 0.2096 F-statistic: 246.8 on 1 and 926 DF, p-value: < 2.2e-16 直線的斜率 = 這條回歸線summary中的 parent ~ Estimate 的值 = 0.64629 斜率的標準差 = summary 中的 parent ~ Std.Error 的值 = 0.04114

plot(jitter(child,4) ~ parent, galton) regrline <- lm(child ~ parent, galton) abline(regrline,lwd=3, col=‘red‘) summary(regrline)
學習筆記 | 回歸模型 | 01 介紹
