在前一篇文章中，我們討論了循環的分析。許多算法本質上是遞歸的。當我們分析它們時，我們得到時間復雜度的遞歸關系。我們得到的運行時間是大小為n的輸入作為n的函數，以及較小大小的輸入的運行時間。例如在“ 合並排序”中，為了對給定的數組進行排序，我們將其分成兩半，並遞歸地重復兩個進程。最後我們合並結果。合並排序的時間復雜度可以寫為T（n）= 2T（n / 2）+ cn。還有很多其他算法，如二進制搜索，河內塔等。

主要有三種解決復發的方法。

1）替代方法：我們猜測解，然後我們使用數學歸納來證明猜測是正確的或不正確的。

For example consider the recurrence T(n) = 2T(n/2
 
) + n

We guess the solution as T(n) = O(nLogn). Now we use induction
to prove our guess.

We need to prove that T(n) <= cnLogn. We can assume that it is true
for values smaller than n.

T(n) = 2T(n/2) + n
    <= cn/2Log(n/2) + n
    =  cnLogn - cnLog2 + n
    =  cnLogn - cn + n
    <= cnLogn

2）重復樹法：在這種方法中，我們繪制一個重復樹，並計算每個級別的樹所花費的時間。最後，我們總結了各級的工作。為了繪制復發樹，我們從給定的復現開始，繼續繪制，直到我們在各個層次之間找到一個模式。該圖案通常是算術或幾何系列。

For example consider the recurrence relation 
T(n) = T(n/4) + T(n/2) + cn2

           cn2
         /           T(n/4)     T(n/2)

If we further break down the expression T(n/4) and T(n/2), 
we 
 
get following recursion tree.

                cn2
           /           \      
       c(n2)/16      c(n2)/4
      /      \          /       T(n/16)     T(n/8)  T(n/8)    T(n/4) 
Breaking down further gives us following
                 cn2
            /            \      
       c(n2)/16          c(n2)/4
       /      \            /      c(n2)/256   c(n2)/64  c(n2)/64    c(n2)/16
 /    \      /    \    /    \       /    \  

To know the value of T(n), we need to calculate sum of tree 
nodes level by level. If we sum the above tree level by level, 
we get the following series
T(n)  = c(n^2 + 5(n^2)/16 + 25(n^2)/256) + ....
The above series is geometrical progression with ratio 5/16.

To get an upper bound, we can sum the infinite series. 
We get the sum as (n2)/(1 - 5/16) which is O(n2)

3）主方法：
主方法是獲得解決方案的直接方法。主方法僅適用於以下類型的復現或可以轉換為以下類型的重復。

T(n) = aT(n/b) + f(n) where a >= 1 and b > 1

有以下三種情況：

1.如果f（n）=Θ（n c）其中c <Log b a則T（n）=Θ（n Log b a）

2.如果F（N）=Θ（N ?）其中c =日誌b一則T（N）=Θ（N ? log n）的

3.如果F（N）=Θ（N ?）其中c>日誌b一則T（N）=Θ（F（N））

這個怎麽用？
主方法主要來源於遞歸樹法。如果我們繪制T（n）= aT（n / b）+ f（n）的遞歸樹，我們可以看到在根處完成的工作是f（n），所有葉子的工作都是Θ（n c） c是日誌b a。而遞歸樹的高度為Log bn 在遞歸樹方法中，我們計算完成的總工作量。如果在葉子上完成的工作多數多，那麽葉子是主要的部分，我們的結果就成為樹葉上的工作（情況1）。如果在葉子和根部的工作是漸進的，那麽我們的結果就變成了高度乘以任何級別的工作（情況2）。如果在根處完成的工作是漸近的，那麽我們的結果就會在根目錄下完成（情況3）。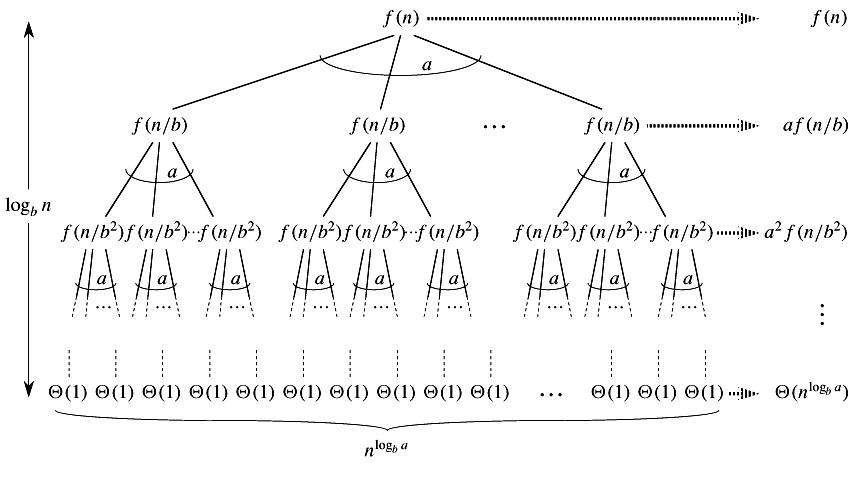

使用主方法
合並排序：T（n）= 2T（n / 2）+Θ（n）可以評估其時間復雜度的一些標準算法的示例。情況2由於c為1，Log b a]也為1.因此解為Θ（n Logn）

二進制搜索：T（n）= T（n / 2）+Θ（1）。情況2也在c為0且Log b a也為0的情況下出現。因此解為Θ（Logn）

註意：
1）使用主定理可以解決形式T（n）= aT（n / b）+ f（n）的復現。給定的三例在他們之間有一些差距。例如，使用主方法不能求解重復T（n）= 2T（n / 2）+ n / Logn。

2）情況2可以擴展為f（n）=Θ（n c Log k n）
如果f（n）=Θ（n c Log k n）對於一些常數k> = 0，c = Log b a，則T（n）=Θ（n c Log k + 1 n）

算法分析| 系列4（解決遞推）