一、前言

如果需要Java版本的堆排序或者堆排序的基礎知識——樹的概念，請參看本人博文《排序算法（二）堆排序》

關於選擇排序的問題

選擇排序最大的問題，就是不能知道待排序數據是否已經有序，比較了所有數據也沒有在比較中確定數據的順序。

堆排序對簡單選擇排序進行了改進。

二、準備知識

堆：它是一個完全二叉樹

大頂堆：每個非葉子結點都要大於或者等於其左右孩子結點的值稱為大頂堆

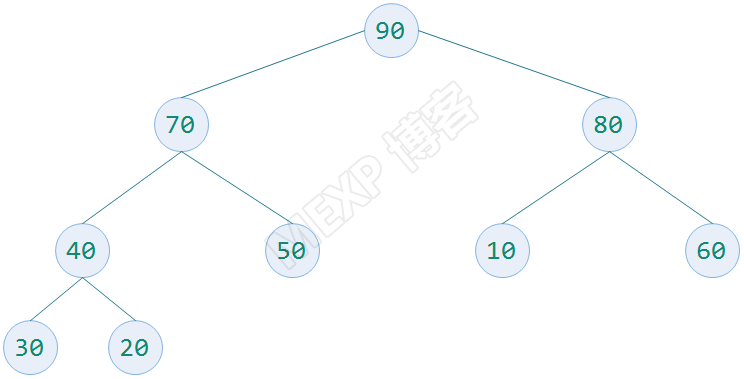
小頂堆：每個非葉子結點都要小於或者等於其左右孩子結點的值稱為小頂堆

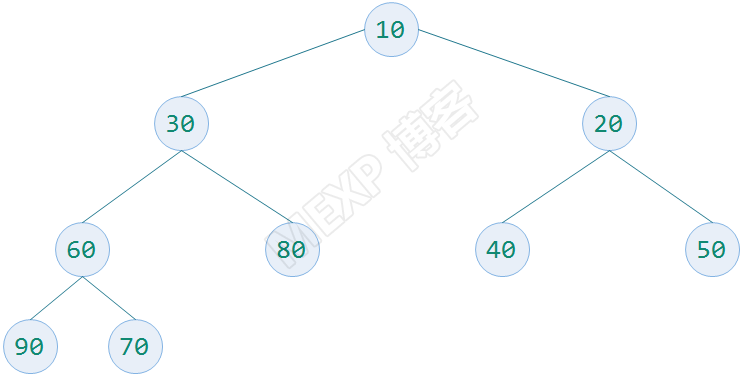
三、算法思路

堆排序大致可以分為下面幾個步驟：

1、構建完全二叉樹

將原始數據放入完全二叉樹中

2、構建大頂堆

需要選擇起點結點，選擇下一個結點，以及如何調整堆

3、排序

將堆頂數據依次拿走，生成排序的樹，最後用層序遍歷就可以難道所有的排序元素

四、算法實現

（一）構建完全二叉樹

待排序數字為 30,20,80,40,50,10,60,70,90

構建一個完全二叉樹存放數據，並根據性質5對元素編號，放入順序的數據結構中

構造一個列表為[0,30,20,80,40,50,10,60,70,90]，用它來描述完全二叉樹

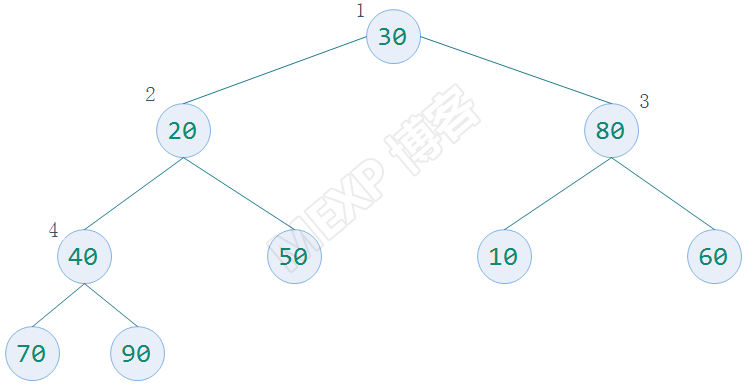
（二）打印樹（輔助函數）

為了方便觀察，生成一個打印列表為樹結構的函數，方便觀察樹結點的變動，不屬於算法函數

為了適應不同的完全二叉樹，這個打印函數還需要特殊處理一下。

思路：

第一行取1個，第二行取2個，第三行取3個，以此類推

投影來思考一個類柵格系統，就可以很好的打印這個樹了

import math
def print_tree(array):
    ‘‘‘
        前空格元素間
    170
    237
    313
    4   01
    ‘‘‘
    index = 1
    depth = math.ceil(math.log2(len(array))) # 因為補0了，不然應該是math.ceil(math.log2(len(array)+1))
    sep = ‘  ‘
    for i in range(depth):
        offset = 2 ** i
        print(sep * (2 ** (depth - i - 1) - 1), end=‘‘)
        line = array[index:index + offset]
        for j, x in enumerate(line):
            print("{:>{}}".format(x, len(sep)), end=‘‘)
            interval = 0 if i == 0 else 2 ** (depth - i) - 1
            if j < len(line) - 1:
                print(sep * interval, end=‘‘)
        index += offset
        print()
print_tree([0, 30, 20, 80, 40, 50, 10, 60, 70, 90, 22])
print_tree([0, 30, 20, 80, 40, 50, 10, 60, 70, 90, 22, 33, 44, 55, 66, 77])
print_tree([0, 30, 20, 80, 40, 50, 10, 60, 70, 90, 22, 33, 44, 55, 66, 77, 88, 99, 11])

（三）構建大頂堆

核心算法

對於堆排序的核心算法就是堆結點的調整

1. 度數為2的結點A，如果它的左右孩子結點的最大值比它大的，將這個最大值和該結點交換

2. 度數為1的結點A，如果它的左孩子的值大於它，則交換

3. 如果結點A被交換到新的位置，還需要和其孩子結點重復上面的過程

核心算法實現如下：

# 為了和編碼對應，增加一個無用的0在首位
origin = [0, 30, 20, 80, 40, 50, 10, 60, 70, 90]
total = len(origin) - 1  # 初始待排序元素個數，即n
print(origin)
print_tree(origin)
def heap_adjust(n, i, array: list):
    ‘‘‘
    調整當前結點(核心算法)
    調整的結點的起點在n//2，保證所有調整的結點都有孩子結點
    :param n: 待比較數個數
    :param i: 當前結點的下標
    :param array: 待排序數據
    :return: None
    ‘‘‘
    while 2 * i <= n:
        # 孩子結點判斷 2i為左孩子，2i+1為右孩子
        lchile_index = 2 * i
        max_child_index = lchile_index  # n=2i
        if n > lchile_index and array[lchile_index + 1] > array[lchile_index]:  # n>2i說明還有右孩子
            max_child_index = lchile_index + 1  # n=2i+1
        # 和子樹的根結點比較
        if array[max_child_index] > array[i]:
            array[i], array[max_child_index] = array[max_child_index], array[i]
            i = max_child_index  # 被交換後，需要判斷是否還需要調整
        else:
            break
        # print_tree(array)
heap_adjust(total, total // 2, origin)
print(origin)
print_tree(origin)

到目前為止也只是解決了單個結點的調整，下面要使用循環來依次解決解決比起始結點編號小的結點。

起點的選擇

從最下層最右邊葉子結點的父結點開始

由於構造了一個前置的0，所以編號和列表的索引正好重合

但是，元素個數等於長度減1

下一個結點

按照二叉樹性質5編號的結點，從起點開始找編號逐個遞減的結點，直到編號1

# 構建大頂堆、大根堆
def max_heap(total,array:list):
    for i in range(total//2,0,-1):
        heap_adjust(total,i,array)
    return array
print_tree(max_heap(total,origin))

（四）排序

思路

1. 每次都要讓堆頂的元素和最後一個結點交換，然後排除最後一個元素，形成一個新的被破壞的堆。

2. 讓它重新調整，調整後，堆頂一定是最大的元素。

3. 再次重復第1、2步直至剩余一個元素

def sort(total, array:list):
    while total > 1:
        array[1], array[total] = array[total], array[1] # 堆頂和最後一個結點交換
        total -= 1
        heap_adjust(total,1,array)
    return array
print_tree(sort(total,origin))

改進

如果最後剩余2個元素的時候，如果後一個結點比堆頂大，就不用調整了。

def sort(total, array:list):
    while total > 1:
        array[1], array[total] = array[total], array[1] # 堆頂和最後一個結點交換
        total -= 1
        if total == 2 and array[total] >= array[total-1]:
            break
        heap_adjust(total,1,array)
    return array
print_tree(sort(total,origin))

五、算法分析

1、利用堆性質的一種選擇排序，在堆頂選出最大值或者最小值

2、時間復雜度

堆排序的時間復雜度為O(nlogn)

由於堆排序對原始記錄的排序狀態並不敏感，因此它無論是最好、最壞和平均時間復雜度均為O(nlogn)

3、空間復雜度

只是使用了一個交換用的空間，空間復雜度就是O(1)

4、穩定性

不穩定的排序算法

六、完整代碼

如果有需要，請自行將算法函數封裝成類。

import math
def print_tree(array):
    ‘‘‘
        前空格元素間
    170
    237
    313
    4   01
    ‘‘‘
    index = 1
    depth = math.ceil(math.log2(len(array))) # 因為補0了，不然應該是math.ceil(math.log2(len(array)+1))
    sep = ‘  ‘
    for i in range(depth):
        offset = 2 ** i
        print(sep * (2 ** (depth - i - 1) - 1), end=‘‘)
        line = array[index:index + offset]
        for j, x in enumerate(line):
            print("{:>{}}".format(x, len(sep)), end=‘‘)
            interval = 0 if i == 0 else 2 ** (depth - i) - 1
            if j < len(line) - 1:
                print(sep * interval, end=‘‘)
        index += offset
        print()
# Heap Sort
# 為了和編碼對應，增加一個無用的0在首位
origin = [0, 30, 20, 80, 40, 50, 10, 60, 70, 90]
total = len(origin) - 1  # 初始待排序元素個數，即n
print(origin)
print_tree(origin)
print("="*50)
def heap_adjust(n, i, array: list):
    ‘‘‘
    調整當前結點(核心算法)
    調整的結點的起點在n//2，保證所有調整的結點都有孩子結點
    :param n: 待比較數個數
    :param i: 當前結點的下標
    :param array: 待排序數據
    :return: None
    ‘‘‘
    while 2 * i <= n:
        # 孩子結點判斷 2i為左孩子，2i+1為右孩子
        lchile_index = 2 * i
        max_child_index = lchile_index  # n=2i
        if n > lchile_index and array[lchile_index + 1] > array[lchile_index]:  # n>2i說明還有右孩子
            max_child_index = lchile_index + 1  # n=2i+1
        # 和子樹的根結點比較
        if array[max_child_index] > array[i]:
            array[i], array[max_child_index] = array[max_child_index], array[i]
            i = max_child_index  # 被交換後，需要判斷是否還需要調整
        else:
            break
    # print_tree(array)
# 構建大頂堆、大根堆
def max_heap(total,array:list):
    for i in range(total//2,0,-1):
        heap_adjust(total,i,array)
    return array
print_tree(max_heap(total,origin))
print("="*50)
# 排序
def sort(total, array:list):
    while total > 1:
        array[1], array[total] = array[total], array[1] # 堆頂和最後一個結點交換
        total -= 1
        if total == 2 and array[total] >= array[total-1]:
            break
        heap_adjust(total,1,array)
    return array
print_tree(sort(total,origin))
print(origin)

本文出自 “終南山下” 博客，謝絕轉載！

排序算法（四）堆排序的Python實現及算法詳解