Chapter 1 Regression: Predicting and Relating Quantitative Features

1.1 統計學，數據分析，回歸

統計學是利用數學來研究和提高從不完整的，有噪聲、corrupt、不可復制的和其他因素導致的不完美的數據中刻畫可靠的推論的方法。

Paragraph 1 end =================

大多數的科學的學科都是圍繞著我們世界的某個部分，或者是我們之中的。

心理學（Psychology）研究思想；地理學（geology）研究地球的組成和形成；經濟學研究生產，分配和交換；真菌學（mycology）研究蘑菇。統計學並不研究世界，而是研究我們試圖去理解世界的方法——某些供其他學科使用的智慧工具。它的作用並不直觀，而是通過幫助其他學科來體現價值。

Paragraph 2 end =================

這種用途是十分重要的，因為所有的學科都必須處理不完美的數據。數據也許並不完美，因為我們只能觀察和記錄到相關數據的其中一小部分；或者因為，不管我們不管我們多麽仔細地嘗試，我們的數據總是會包含噪聲。在過去的兩個世紀中，統計學通過將它們建模成為隨機過程來處理所有的這些不完美，並且概率已經稱為統計學的中心以至於我們必須刻意的（deliberately）介紹隨機事件（as in sample surveys）。

Paragraph 3 end =================

統計學就使用概率論來對數據建模得出推論。我們試圖使用數學方式去理解不同過程的來得到推論：在何種條件下它們是可靠的？它們會產生哪種誤差，誤差頻率是多少？當它們有效的時候我們能得到什麽？當某些東西出差錯的時候會有什麽跡象？就像其他的科學一樣，比如工程，藥學和經濟學，統計學不僅僅在於理解，同時也回去改善：我們想要更好的分析數據，更加可靠地，有更少更小的誤差，能夠在更廣泛的條件下，更快地，付出更少的體力勞動。有時候這些目標會產生矛盾——快速、簡單的方法也許很容易出錯（error-prone），或者說在非常狹隘的條件下才會很可靠。

Paragraph 4 end ================

人們很想知道的是，不同的變量之間是如何關聯的，並且統計學中提供的一個核心工具用來了解變量之間的關系就是回歸。在36-401（課程）中，你已經學會了如何進行線性回歸，了解到了它如何用於數據分析中，也學習了它的屬性。在本課程中，我們將在此基礎之上構建，在很多方向上擴展基本的線性回歸，來回答很多關於變量之間如果關聯的問題。

Paragraph 5 end ================

這和預測密切相關。能夠預測並不是我們想要知道變量之間關系的唯一原因，有時預測也可以測試我們對於關系的認識。（如果我們理解錯了，我們也許仍可以預測，但是很難發現我們如何理解並且不能預測。）所以在超越線性回歸的知識之前，先來看一下預測，並且如何從一無所有來預測一個一個變量。然後我們來看一下在變量之間的預測性關系，並且會發現線性回歸只是smoothing方法這個大家族中的一個成員而已，這類方法我們都可以使用。

Paragraph 6 end ====================

Section 1.1 end ===================

1.2 猜測隨機變量的值

我們有一個數值的，數量的隨機變量，我們想象設為Y。我們假設它是一個隨機變量，並且試圖通過通過猜測一個單值來預測它。（其他類型的預測也是可能的——我們也許會猜測Y是否會落入到某個範圍之內，或者它會有其他的可能性，又或者是Y的整個概率分布。但是在後面的課中我們將會學到這也將適用於其他類型的預測。）猜測的最好的值是什麽？或者更正常的，Y的最佳預測點是哪個？

Paragraph 7 end ================

為了回答這個問題，我們需要挑選一個函數來進行優化，用來度量我們預測結果的好壞——或者說我們預測的結果有多差，我們得到的誤差是多大。一個合理的起點是均方誤差（mean squared error）：

因此，我們想要找到一個值，r，使得MSE(a)最小。

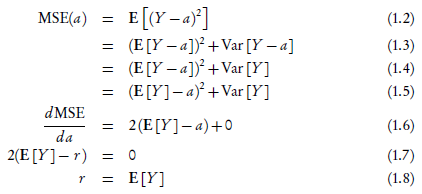
因此這裏我們用均方誤差來度量了我們的預測質量，最佳的預測值就是期望值。

1.2.1 預測期望值

當然，為了預測E[Y]，我們必須知道Y的期望值。事實上，我們並不知道。然後，如果我們有采樣值y1, y2, ..., yn，我們可以從采樣的平均值來預測期望：

如果采樣的數據是獨立同分布的（independent and identically distributed，IID），那麽打書定理告訴我們：

並且中心極限定理告訴我們有關於收斂速度的快慢（即平方誤差大概是Var[Y]/n）。

當然假設yi是獨立同分布的這是一個很強的條件，但是我們可以假設幾乎一樣的條件，如果它們對於共同的期望值是不相關的。即使它們是相關的，但是相關性減少的足夠快，所有的改變為收斂速度。因此"坐下，等著，收斂"是一個預測期望值的非常可靠的方法。

1.3 回歸函數

當然，通常預測一個點的值並不十分有用。典型的，在數據中我們有很多的變量。

來學學數據分析吧（二）第一章 預測和關聯數量特征