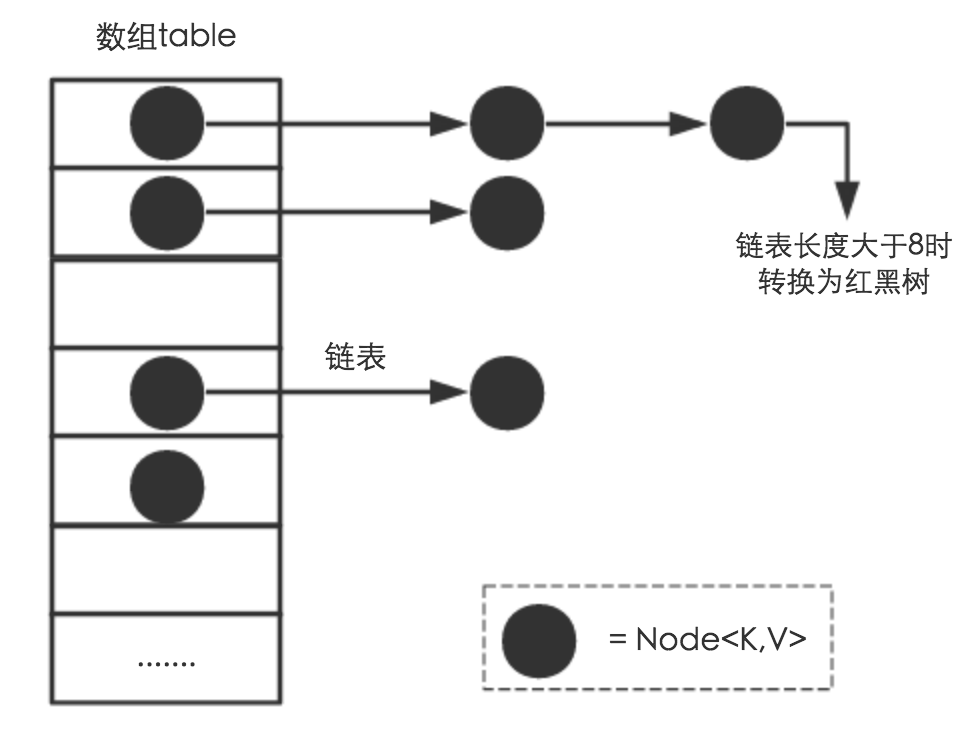
樹節點 技術 edm 也會 你會 當前 包含 反射 images

HashMap通常使用鏈地址方法存儲，但是當鏈的長度太大（大於8）時，這個鏈就會轉換為紅黑樹，類似java.util.TeeMap。大部分的方法一般使用鏈表，但檢查到節點為樹節點時，也會使用樹。樹狀的鏈表可以向其他鏈表一樣使用和遍歷，但是如何HashMap中沖突嚴重的情況下，樹狀的鏈表查找更快。HashMap中的鏈表多以單鏈表為主，查找當前鏈表是否是樹一般會造成延遲。 樹鏈表按hashCode的值排列，但是為了以防萬一，如何兩個元素的hashCode相同，且他們都實現了Comparable<C>接口，則他們的compareTo方法會用作比較。我們一般通過反射來驗證元素的類型。樹狀鏈表雖然增加了結構的復雜度，但是也提高了查找效率O(log n)。因此在hashCode分布不太好（均勻分布的hashCode為最好）時，或者是好多元素具有同一個hashCode，只要他們是可比較的，Hashmap的性能就不會下降很多。 如果我們沒有將會讓費2倍的時間和空間。但是對於poor user 編寫的程序已經很慢了，這些也優化也起不到什麽作用。 因為樹的節點比鏈表大小要大兩倍，所以只有在鏈表的節點很大時，我們才使用紅黑樹存儲。當紅黑樹很小時，又會轉成普通的鏈表存儲。如何hashCode分布很好的話，紅黑樹時很少會用到的。理想情況下使用隨機的hashCode，而且節點的分布服從泊松分布 紅黑樹的根是他的第一個節點，但是有時候樹根也不是其第一個元素（使用了Iterator.remove）樹根就變成其他的元素了，但使用TreeNode.root()方法就可以恢復。

1，HashMap對於自己的結構性改變（結構性改變值添加或刪除一個鍵值組合等，只要不是修改某個key對應的value都認為是結構性的改變）不是線程同步的， 如果要實現線程同步需要在新建HashMap時，這樣寫： Map m = Collectons.synchronizedMap(new HashMap(...)); 如果創建了Iterator，且在遍歷的過程中刪除了某個元素，Iterator就會包ConcurrentModificationExeption。 在HashMap中的get方法中你會看到一種特別奇怪的寫法，從table中取數時，table[(n-1)&hash]，根據“與”運算分析，這是一種取余的方法，(n-1)&hash得到的數永遠小於n-1，這裏又學到了一種獲得小於等於某個數的新算法。 public class Test { public static void main(String[] args) { int a = 12; for(int i = 0; i < 100; i ++){ if((i&a)>=a) { System.out.println(i + "->" + (i&a)); } } } } 12->12 13->12 14->12 15->12 ... 61->12 62->12 同時查看了其在地址中沖突的概率 public class Test { public static void main(String[] args) { boolean[] flags = new boolean[100]; for(boolean b : flags) { b = false; } int a = 100; for(Integer i = 0; i < 100; i ++){ if(flags[(a-1)&hash(new String(i+""))]) { System.out.println(i + "---crash--->" + ((a-1)&hash(i))); } else { flags[(a-1)&hash(i)] = true; } } } public static int hash(Object key) { int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); } } 發現其沖突率還是很高的 10---crash--->2 44---crash--->32 45---crash--->33 46---crash--->34 47---crash--->35 48---crash--->32 49---crash--->33 50---crash--->34 51---crash--->35 52---crash--->32 53---crash--->33 .... 99---crash--->99 如果沖突，HashMap使用鏈表或 紅黑樹存儲沖突後的節點。見如下代碼解析： /** * Implements Map.put and related methods * * @param hash hash for key * @param key the key * @param value the value to put * @param onlyIfAbsent if true, don‘t change existing value * @param evict if false, the table is in creation mode. * @return previous value, or null if none */ final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; //如果table為空，或者length=0，即沒有數據，要resize()擴容 //Map剛創建完成時會走這段邏輯 if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; //如果算出的table對應位置沒有數，就將其放到該位置上 if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); //如果沖突，要在這個節點上構造平衡樹，並將數據存儲到這棵樹上 else { Node<K,V> e; K k; //如果當前節點的hash值相同，key也相同，則將該節點替換 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; //如果當前節點為平衡樹節點，遍歷平衡樹，並將該值掛到樹上 else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); else { //遍歷類似鏈表的結構，如果找到鏈表的尾部，且沒有超過最大長度放到鏈表上 for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //如果超過最大長度，則放到treeify（紅黑樹）結構上 treeifyBin(tab, hash); break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) resize(); afterNodeInsertion(evict); return null; } HashMap不是線程安全的，但是在讀HashMap中的值時，其結構發生了變化，則會拋出 ConcurrentModificationException 她是通過自身的私有變量modCount控制的，modCount很像HashMap的版本號，如果其結構發生變化modCount的值肯定發生變化，代表一個新版本的HashMap產生了。 HashMap中有一個函數，用來計算比給定值大的第一個2的冪次方數 static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; } int數值占用4個字節，32bit。該算法的思路是，用給定值的最高位的1，將其最高位右邊的位都填充為1。然後在加上1。 例如 cap = 20 n = cap - 1 = 19 0001 0011 n>>>1 = 0000 1001 n|=n>>>1 = 0001 1011 n>>>2 = 0000 0110 n|=n>>>2 = 0001 1111 n>>>4 = 0000 0001 n|=n>>>4= 0001 1111 n>>>8 與 n >>>16 都為0 所以最後的結果為 31（0001 1111） + 1 =32 table的size要是2的冪級數，是為了在resize()的時，對於某個node，要麽不移動，要麽移動到其位置*2的地方。 在resize()函數中有這樣一段代碼： next = e.next; // 如果e.hash 小於 oldCap 不移動存儲的位置 if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } else { // 如果 e.hash >= oldCap 要移動存儲的位置 if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); if (loTail != null) { loTail.next = null; newTab[j] = loHead; } if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; } 可以看出上面代碼中設計到兩個鏈表（loHead，loTail）和（hiHead，hiTail）。每一次循環都是往某個鏈表中添加一個元素。重點是為什麽要弄兩個鏈表。這是因為table中前半部分的element是不用移動的。 假設原來的capacity = 16 在往table中放數據時。都是e.hash&(capacity-1) ，數據都存放到0至15的位置。假設原來有一個element.hash < 16 則 e.hash&capacity == 0 。這裏我們就明白了，原來table前部中的元素是不需要移動的。如果原來鏈表中存儲著e.hash >= 16 的，這是在 e.hash & capacity != 0 這時就將其存儲到table的後半部分。因為在resize()時調用的時oldCap == 16 當table.length = 32 時，我們假設原來有一個元素 e.hash ==18 e.hash & oldCap == 2，當再次分配時，會走（hiHead，hiTail）這段邏輯，放在角標為16+2 的位置。當擴容完成，我們用新的容量取余時，會計算的到18。證明在擴容時放數據的位置沒有問題。 當節點為TreeNode時，調用TreeNode的split方法。在處理樹節點時，也是先按鏈表處理，然後在重構成樹。 TreeNode與Node之間的繼承關系： 而且TreeNode中有一個變量prev //bit 當前table長度 //e 當前樹節點 for (TreeNode<K,V> e = b, next; e != null; e = next) { next = (TreeNode<K,V>)e.next; e.next = null; //如果e.hash小於當前table的長度， if ((e.hash & bit) == 0) { // 如果loTail為空，說明當前鏈表中沒有數據 if ((e.prev = loTail) == null) //數據頭即為e loHead = e; else loTail.next = e; // 每次添加一個節點就將loTail指向當前節點 loTail = e; // 計數器 +1 為了根據這個數值的大小決定存儲成樹形，還是鏈表 ++lc; } else { // 如果 e.hash >= 當前table的長度 // 如果當前鏈表中沒有數據 if ((e.prev = hiTail) == null) // 將數據頭指向當前節點 hiHead = e; else // 如果當前鏈表不為空，則在鏈表的尾部加上一個節點 hiTail.next = e; // 尾部永遠指向最後添加的節點 hiTail = e; ++hc; } } // 當前鏈表遍歷完成後，根據計數器決定其存成什麽樣子。 if (loHead != null) { if (lc <= UNTREEIFY_THRESHOLD) tab[index] = loHead.untreeify(map); else { tab[index] = loHead; if (hiHead != null) // (else is already treeified) loHead.treeify(tab); } } if (hiHead != null) { if (hc <= UNTREEIFY_THRESHOLD) tab[index + bit] = hiHead.untreeify(map); else { tab[index + bit] = hiHead; if (loHead != null) hiHead.treeify(tab); } 下面就應該看treeify(tab)的實現了，這個實現就是將單向鏈表轉換為紅黑樹的過程。 final void treeify(Node<K,V>[] tab) { TreeNode<K,V> root = null; //當前節點為x for (TreeNode<K,V> x = this, next; x != null; x = next) { // next為下一個節點 next = (TreeNode<K,V>)x.next; // 當前節點的左右子節點清空 x.left = x.right = null; // 第一次進入時，根為空，這是給根賦值，且將根節點標記為黑色 if (root == null) { x.parent = null; x.red = false; root = x; } // 如果不是第一次進入 else { K k = x.key; int h = x.hash; Class<?> kc = null; for (TreeNode<K,V> p = root;;) { int dir, ph; K pk = p.key; // 如果根節點的hash比當前節點的hash大 if ((ph = p.hash) > h) dir = -1; //存到左邊 else if (ph < h) dir = 1; // 存到右邊 else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); TreeNode<K,V> xp = p; // 如果dir < 0 且 p 指向根節點的左子節點，如果dir > 0 p 指向根節點的右子節點 // 如果 p 指向的子節點為空，則要存入樹中的節點存入子節點，否則，p指向其某個子節點，然後重復for循環 if ((p = (dir <= 0) ? p.left : p.right) == null) { // 當前節點的父節點為根節點 x.parent = xp; // 根據dir 將x存入根節點的子節點中 if (dir <= 0) xp.left = x; else xp.right = x; // 保證樹的平衡 root = balanceInsertion(root, x); break; } } } } moveRootToFront(tab, root); } 這篇文章對看懂紅黑樹插入數據操作有用：https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91 HashMap為什麽使用紅黑樹而不使用平衡樹呢？ 1. 如果插入一個node引起了樹的不平衡，AVL和RB-Tree都是最多只需要2次旋轉操作，即兩者都是O(1)；但是在刪除node引起樹的不平衡時，最壞情況下，AVL需要維護從被刪node到root這條路徑上所有node的平衡性，因此需要旋轉的量級O(logN)，而RB-Tree最多只需3次旋轉，只需要O(1)的復雜度。 2. 其次，AVL的結構相較RB-Tree來說更為平衡，在插入和刪除node更容易引起Tree的unbalance，因此在大量數據需要插入或者刪除時，AVL需要rebalance的頻率會更高。因此，RB-Tree在需要大量插入和刪除node的場景下，效率更高。自然，由於AVL高度平衡，因此AVL的search效率更高。 3. map的實現只是折衷了兩者在search、insert以及delete下的效率。總體來說，RB-tree的統計性能是高於AVL的。 作者：知乎用戶 鏈接：https://www.zhihu.com/question/20545708/answer/58717264 來源：知乎 著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請註明出處。 紅黑樹為滿足如下條件的二叉搜索樹： 1. 每個結點或者為黑色或者為紅色。 2. 根結點為黑色。 3. 每個葉結點(實際上就是NULL指針)都是黑色的。 4. 如果一個結點是紅色的，那麽它的兩個子節點都是黑色的（也就是說，不能有兩個相鄰的紅色結點）。 5. 對於每個結點，從該結點到其所有子孫葉結點的路徑中所包含的黑色結點數量必須相同。 下面是關於刪除元素的代碼解釋： /** * Implements Map.remove and related methods * * @param hash hash for key * @param key the key * @param value the value to match if matchValue, else ignored * @param matchValue if true only remove if value is equal * @param movable if false do not move other nodes while removing * @return the node, or null if none */ final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) { Node<K,V>[] tab; Node<K,V> p; int n, index; // 如果table為空，或沒有數據，或者某有節點的給定hash沒有對應的元素，則直接返回空 if ((tab = table) != null && (n = tab.length) > 0 && (p = tab[index = (n - 1) & hash]) != null) { Node<K,V> node = null, e; K k; V v; // 如果找到這樣一個節點的hash,key 都和給定的值相等，則將其記錄到node中 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) node = p; // 否則 如果其有下一個節點 else if ((e = p.next) != null) { if (p instanceof TreeNode) // 如果當前節點存的是樹，則直接從樹種找 node = ((TreeNode<K,V>)p).getTreeNode(hash, key); // 否則即為鏈表，從鏈表中查找 else { do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) { node = e; break; } p = e; // p一直指向e的前一個節點 } while ((e = e.next) != null); } } // node != null 表示找到了對應的節點，如果要值相等，這值相等，否則值不等於空，且值也要相等 if (node != null && (!matchValue || (v = node.value) == value || (value != null && value.equals(v)))) { // 如果當前節點為樹，則要從樹種移除 if (node instanceof TreeNode) ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable); // 如果是鏈表中的第一個節點，tab[index]存鏈表頭的地方指向其下一個節點 else if (node == p) tab[index] = node.next; else // 否則 將找到的節點從鏈表中刪除 p.next = node.next; // p一直指向e的前一個節點 ++modCount; --size; afterNodeRemoval(node); return node; } } return null; } 關於紅黑樹的旋轉建議百度

HashMap源碼解讀