測試 1
立方數(cubic)
Time Limit:1000ms Memory Limit:128MB
題目描述
LYK定義了一個數叫“立方數”,若一個數可以被寫作是一個正整數的3次方,則這個數就是立方數,例如1,8,27就是最小的3個立方數。
現在給定一個數P,LYK想要知道這個數是不是立方數。
當然你有可能隨機輸出一些莫名其妙的東西來騙分,因此LYK有T次詢問~
輸入格式(cubic.in)
第一行一個數T,表示有T組數據。
接下來T行,每行一個數P。
輸出格式(cubic.out)
輸出T行,對於每個數如果是立方數,輸出“YES”,否則輸出“NO”。
輸入樣例
3
8
27
28
輸出樣例
YES
YES
NO
數據範圍
對於30%的數據p<=100。
對於60%的數據p<=10^6。
對於100%的數據p<=10^18,T<=100。
思路:暴力
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int T; long long n; int main(){ freopen("cubic.in","r",stdin); freopen("cubic.out","w",stdout); scanf("%d",&T); while(T--){ bool flag=0; scanf("%I64d",&n); for(long long i=1;i<=1000000;i++) if(i*i*i==n){ cout<<"YES"<<endl; flag=1;break; } if(!flag) cout<<"NO"<<endl; } } /* 3 8 27 28 */
立方數2(cubicp)
Time Limit:1000ms Memory Limit:128MB
題目描述
LYK定義了一個數叫“立方數”,若一個數可以被寫作是一個正整數的3次方,則這個數就是立方數,例如1,8,27就是最小的3個立方數。
LYK還定義了一個數叫“立方差數”,若一個數可以被寫作是兩個立方數的差,則這個數就是“立方差數”,例如7(8-1),26(27-1),19(27-8)都是立方差數。
現在給定一個數P,LYK想要知道這個數是不是立方差數。
當然你有可能隨機輸出一些莫名其妙的東西,因此LYK有T次詢問~
這個問題可能太難了…… 因此LYK規定P是個質數!
輸入格式(cubicp.in)
第一行一個數T,表示有T組數據。
接下來T行,每行一個數P。
輸出格式(cubicp.out)
輸出T行,對於每個數如果是立方差數,輸出“YES”,否則輸出“NO”。
輸入樣例
5
2
3
5
7
11
輸出樣例
NO
NO
NO
YES
NO
數據範圍
對於30%的數據p<=100。
對於60%的數據p<=10^6。
對於100%的數據p<=10^12,T<=100。
思路:

#include<set> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; set<int>se; int T; long long n[1100],maxn; int main(){ freopen("cubicp.in","r",stdin); freopen("cubicp.out","w",stdout); scanf("%d",&T); for(int i=1;i<=T;i++){ scanf("%I64d",&n[i]); maxn=max(maxn,n[i]); } if(maxn<=100){ for(long long int i=1;i<=7;i++) for(long long int j=i+1;j<=7;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } else if(maxn<=1000000){ for(long long int i=1;i<=579;i++) for(long long int j=i+1;j<=579;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } else if(maxn<=2000000){ for(long long int i=1;i<=868;i++) for(long long int j=i+1;j<=868;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } else if(maxn<=3000000){ for(long long int i=1;i<=1001;i++) for(long long int j=i+1;j<=1001;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } else if(maxn<=100000000){ for(long long int i=1;i<=5779;i++) for(long long int j=i+1;j<=5779;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } else{ for(long long int i=1;i<=10000;i++) for(long long int j=i+1;j<=10000;j++){ long long x=j*j*j-i*i*i; if(se.find(x)==se.end()) se.insert(x); } } for(int i=1;i<=T;i++){ if(se.find(n[i])!=se.end()) cout<<"YES"<<endl; else cout<<"NO"<<endl; } } /* 5 2 3 5 7 11 */60分暴力
由立方差公式得: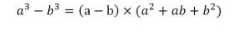 =q
=q
q是質數。
所以(a-b)=1.
a=(b+1)
所以(a^2+ab+b^2)=(b+1)^2+(b+1)*b+b^2=q;
因為q[1,1000000000000]
所以b∈[1,1000000];
暴力枚舉b即可。
#include<cstdio> #include<cstring> #include <iostream> #include<algorithm> using namespace std; int t,flag; long long p; int main(){ freopen("cubicp.in","r",stdin); freopen("cubicp.out","w",stdout); scanf("%d",&t); while(t--){ flag=0; scanf("%I64d",&p); for(int i=1;i<=1e6+10;i++){ if(3ll*i*i+3*i+1==p){ flag=1; break; } if (3ll*i*i+3*i+1>p) break; } if(flag) printf("YES\n"); else printf("NO\n"); } }
猜數字(number)
Time Limit:1000ms Memory Limit:128MB
題目描述
LYK在玩猜數字遊戲。
總共有n個互不相同的正整數,LYK每次猜一段區間的最小值。形如[li,ri]這段區間的數字的最小值一定等於xi。
我們總能構造出一種方案使得LYK滿意。直到…… LYK自己猜的就是矛盾的!
例如LYK猜[1,3]的最小值是2,[1,4]的最小值是3,這顯然就是矛盾的。
你需要告訴LYK,它第幾次猜數字開始就已經矛盾了。
輸入格式(number.in)
第一行兩個數n和T,表示有n個數字,LYK猜了T次。
接下來T行,每行三個數分別表示li,ri和xi。
輸出格式(number.out)
輸出一個數表示第幾次開始出現矛盾,如果一直沒出現矛盾輸出T+1。
輸入樣例
20 4
1 10 7
5 19 7
3 12 8
1 20 1
輸出樣例
3
數據範圍
對於50%的數據n<=8,T<=10。
對於80%的數據n<=1000,T<=1000。
對於100%的數據1<=n,T<=1000000,1<=li<=ri<=n,1<=xi<=n(但並不保證一開始的所有數都是1~n的)。
Hint
建議使用讀入優化
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
for(; !isdigit(ch); ch = getchar()) if(ch == ‘-‘) f = -1;
for(; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + ch - ‘0‘;
return x * f;
}
思路:
第幾次出現矛盾
1.二分,1~mid中出現矛盾 答案一定在1~mid中
1~mid可行 1~mid-1也可行
1~mid不可行 1~mid+1不可行
2.枚舉,每次輸入判斷是否可行
左/右端點進行排序 ×
xi排序 √
從大到小
[l,r]之前被大於x的更大的區間覆蓋過 不可行!!
[1,10] 7&&[5,19] 7-->[5,10] 7
xi相同的進行區間交
從大到小枚舉xi 判斷比xi大的區間的並是否完全覆蓋這個區間
exp:1~5-->9 3~7-->8
2~6-->6 矛盾!!
線段樹!!
並查集維護
O(nlogn*αn)
重點:check
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 1000011 using namespace std; int n,q,ans; int l,r,mid; int fa[MAXN]; struct nond{ int x,y,z; }v[MAXN],tmp[MAXN]; int cmp(nond a,nond b){ return a.z>b.z; } int find(int x){ if(fa[x]==x) return fa[x]; else return fa[x]=find(fa[x]); } bool judge(int k){ int lmin,rmin,lmax,rmax; for(int i=1;i<=n+1;i++) fa[i]=i; for(int i=1;i<=k;i++) tmp[i]=v[i]; sort(tmp+1,tmp+1+k,cmp); lmin=lmax=tmp[1].x; rmin=rmax=tmp[1].y; for(int i=2;i<=k;i++){ if(tmp[i].z<tmp[i-1].z){ if(find(lmax)>rmin) return true; for(int j=find(lmin);j<=rmax;j++) fa[find(j)]=find(rmax+1); lmin=lmax=tmp[i].x; rmin=rmax=tmp[i].y; } else{ lmin=min(lmin,tmp[i].x); lmax=max(lmax,tmp[i].x); rmin=min(rmin,tmp[i].y); rmax=max(rmax,tmp[i].y); if(lmax>rmin) return true; } } if(find(lmax)>rmin) return true; return false; } int main(){ freopen("number.in","r",stdin); freopen("number.out","w",stdout); scanf("%d%d",&n,&q); for(int i=1;i<=q;i++) scanf("%d%d%d",&v[i].x,&v[i].y,&v[i].z); l=1;r=q;ans=q+1; while(l<=r){ mid=(l+r)/2; if(judge(mid)) ans=mid,r=mid-1; else l=mid+1; } cout<<ans; } /* 20 4 1 10 7 5 19 7 3 12 8 1 20 1 */
測試 1

