在學習無向圖的強聯通分量之前

你首先要明白有向圖的強聯通分量

定義

對於任意兩個點，如果存在至少兩條互相不重合的路徑，使得這兩點可以相互到達，那麽這兩個點就屬於同一個強聯通分量

比如說

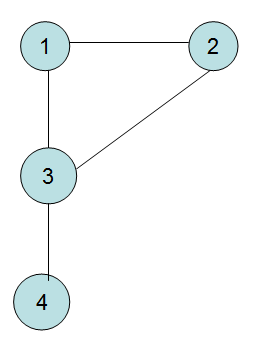
在這張圖中，

$1,2,3$屬於一個強聯通分量

$4$屬於一個強聯通分量，因為$3,4$只有一條可以相互到達的路徑

實現

和有向圖的強聯通分量類似

都是用Tarjan算法實現

在求無向圖的強聯通分量重，我們不允許走已經走過的邊

所以我們在Tarjan的過程中還需要記錄一個father

走的時候只能走目標節點不是father的點

int Tarjan(int now,int fa)
{
	dfn[now]=low[now]=++tot;
	vis[now]=1;
	s.push(now);
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		if(dfn[edge[i].v]==0)	
			Tarjan(edge[i].v,now),low[now]=min(low[now],low[edge[i].v]);
		else if(vis[edge[i].v]&&edge[i].v!=fa)	
			low[now]=min(low[now],dfn[edge[i].v]);
	}
	if(dfn[now]==low[now])
	{
		int top;
		++colornum;
		do
		{
			top=s.top();	color[top]=colornum;
			vis[top]=0;	s.pop();
		}while(top!=now);
	}
}

例題

放一道我們考試的題目

題解點這裏
向下翻到第三題

無向圖的強連通分量