對於卷積的計算需要把握住兩個方向點，第一個是在n點處的累積範圍 ， 第二個是用來做累積的變量的範圍。用下面的實例來說明：

例子1 ：

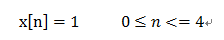
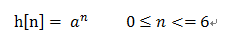
　求兩個信號的卷積？

解 ：

　xn和hn的圖像分別如下所示 ：

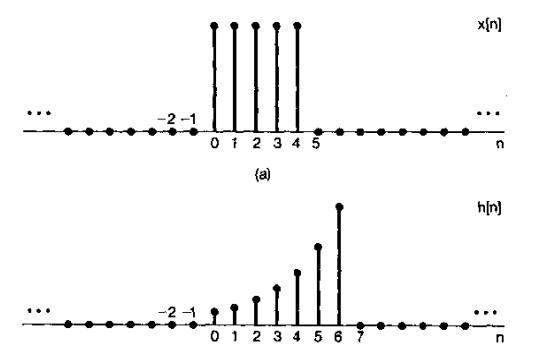
　　這裏需要分情況考慮他們各自的卷積過程分別是在 0<=n<=4 ; 5<=n<=6 ; 7<=n<=10 ; n為其他值的情況，這麽分別考慮的原因是他們在這幾個範圍內的累加變量不一樣：

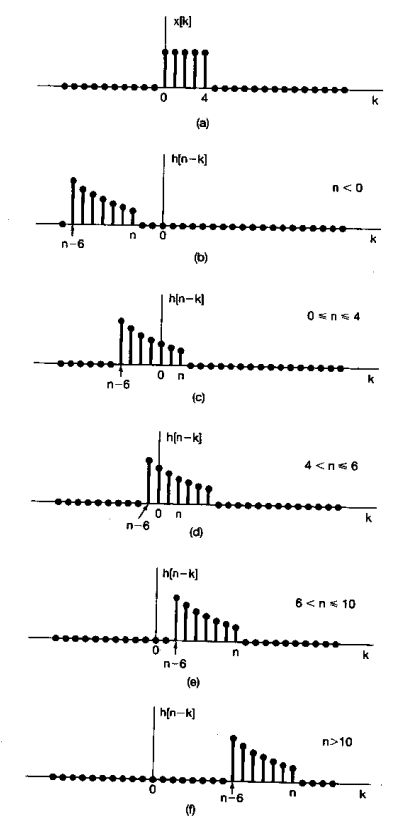
（1）、當 0<=n<=4 ; 對應於每一個n ， 在k軸上的累加方位也是跟隨者n的值增加而增加的，所以：

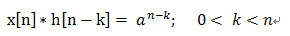
　　 這個表達式表示了在對應n的情況下每一次的值，然後在上式對k的範圍做累積得：

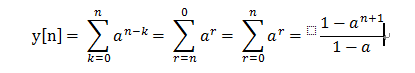
（2）、當 5<=n<=6時，也即x[n]和h[n]在xn的有效範圍之內都是相交的，所以對於k的累積範圍就是 0 <= k <=4

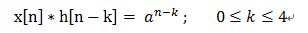
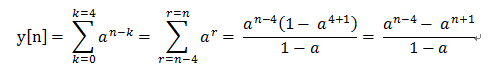
（3）、當 7<=n<=10時，他們之間的有效相交範圍為 n-6 <= k <= 4;

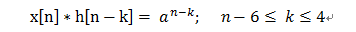
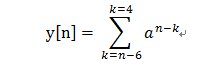
　　　　為了方便計算 ， 令 r = k - n +6;則上式可以寫成

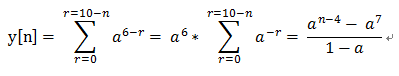
其他的n值y[n] = 0;

例子2： 關於連續信號的卷積計算，同樣需要確定他的積分範圍以及響應的數據

x(t) = 1 ; 0 < t < T

h(t) = t ; 0 < t < 2T

求解兩個信號的卷積？

同樣這個卷積也是要分段來求得，應為對於不同的段，他們的積分變量的上下限是不一樣的，該個主要分成為4段分別為：

0 < k < T ; T < k < 2T ; 2T < k < 2T;

他的輸入和響應圖像如下所示 ：

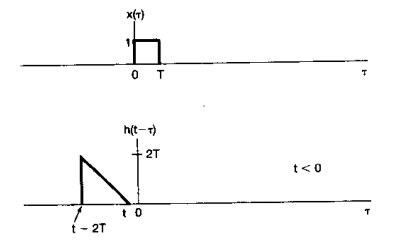
（1）、當 0 < k < T 時，x(k)與h[k]之間重疊的部分是根據t的變化而變化的，也就是說 0 < k < t;

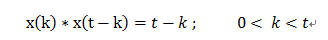
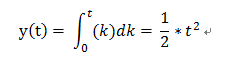
（2）、當 T < k < 2T時，x(k)與h[k]之間重疊的部分是固定的0 - T，也就是說 0 < k < T;

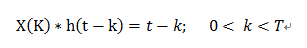
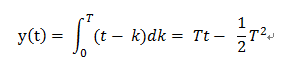
（2）、當 2T < k < 3T時，x(k)與h[k]之間重疊的部分也是根據t的變化而發生變化的，也就是說 t-2T < k < T;

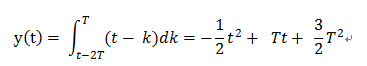
總結 ：

對於這一類的卷積和還是卷積積分，最主要的就是要先搞清楚他在任意n和t值上的卷積的積分上下限以及求和的範圍，有了這個範圍，在對相應的範圍做累積和和積分就可以了。

關於卷積的一個實例