快速排序

思路:

例如：一個列表[5,7,4,6,3,1,2,9,8],

1.首先取第一個元素5,以某種方式使元素5歸位,此時列表被分為兩個部分,左邊的部分都比5小,右邊的部分都比5大,這時列表變成了[2,1,4,3,5,6,7,9,8]
2.再對5左邊進行遞歸排序,取5左邊部分的第一個元素2,使2歸位,這時5左邊的部分變成了[1,2,4,3]
3.2歸位後再對2右邊5左邊的部分即[4,3]進行排序,然後整個列表中5左邊的部分就完成了排序
4.再使用遞歸方法對5右邊的部分進行遞歸排序,直到把列表變成有序列表

列表就變成有序列表了.

代碼實現:

def _quick_sort(data,left,right):
    if left < right:
        mid=partition(data,left,right)
        _quick_sort(data,left,mid-1)
        _quick_sort(data,mid+1,right)

def partition(li,left,right):
    print("befor sort:",li)
    tmp=li[left]

    while left <right:
        while left <right and tmp < li[right]:
            right -=1
        li[left]=li[right]

        while left <right and li[left] < tmp:
            left += 1
        li[right]=li[left]

    li[left]=tmp
    print("after sort:",li)

    return left

def quick_sort(li):
    _quick_sort(li,0,len(li)-1)

li=[5,7,4,6,3,1,2,9,8]
print(quick_sort(li))
 

打印結果:

befor sort: [5, 7, 4, 6, 3, 1, 2, 9, 8]
after sort: [2, 1, 4, 3, 5, 6, 7, 9, 8]
after sort: [1, 2, 4, 3, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
befor sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
befor sort: [1, 2, 3, 4, 5, 6, 7, 9, 8]
after sort: [1, 2, 3, 4, 5, 6, 7, 8, 9]
 

快排的最壞情況:

如果一個列表完全是倒序的,遞歸的次數為最大,等於len(li)*log(len(li))
此時可以隨機取列表中的一個元素進行排序.

堆排序

樹與二叉樹

樹是一種數據結構,比如linux的目錄是呈倒樹狀結構
樹是一種可以遞歸定義的數據結構
樹是由n個節點組成的集合
    如果n=0,那這是一棵空樹
    如果n>0,那存在1個節點作為樹的根節點,其他節點可以分為m個集合,每個集合本身又是一棵樹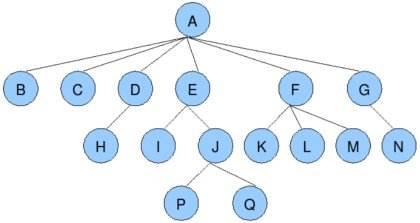

關於樹的一些概念

根節點                     例如 A節點
葉子節點                    例如 B,C,H,I,P,Q等不再分叉的節點
樹的深度(高度)                例如 上圖中的樹共有4層,所以這棵樹的深度為4
子節點/父節點             例如 A,D,E,J等為父節點,B,C,H,I,P為子節點
子樹
 

二叉樹:度不超過2的樹(節點最多有兩個叉)

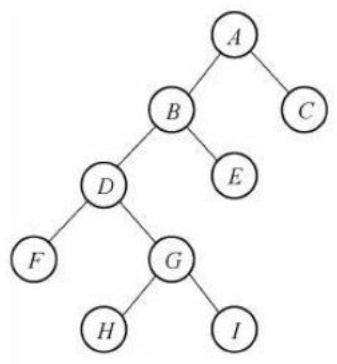
兩種特殊的二叉村
    滿二叉樹:除了葉子節點,所有節點都有兩個子節點,且所有葉子節點的深度都相同
    完全二叉樹:從滿二叉樹的後邊拿走幾個節點,就變成了完全二叉樹,中間不能缺少節點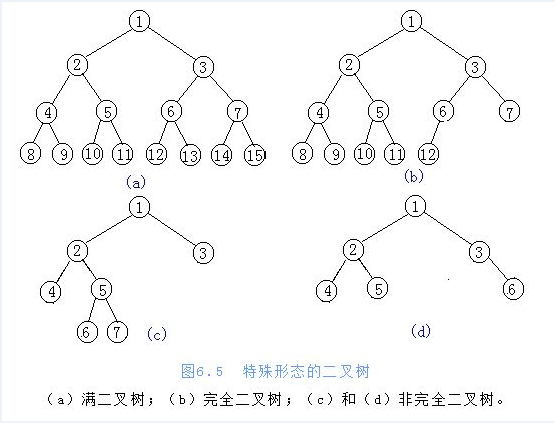

堆排序

大根堆:一棵完全二叉樹,滿足任一節點都比其子節點大

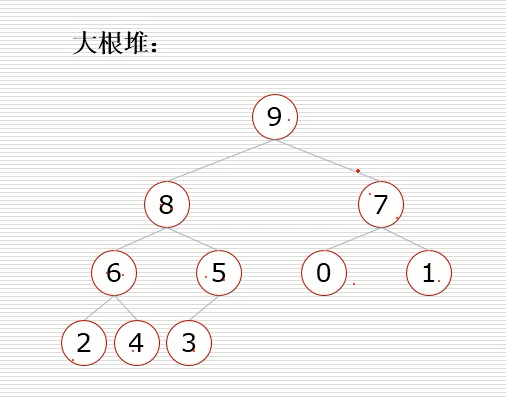
小根堆:一棵完全二叉樹,滿足任一節點都比其子節點小

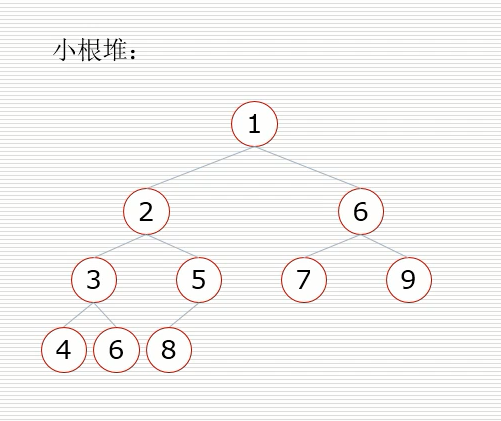
假設節點的左右子樹都是堆,但自身不是堆,

當根節點的左右子樹都是堆時,可以通過一次向下的調整來將其變換成一個堆

構造堆

首先有這樣一棵二叉樹,

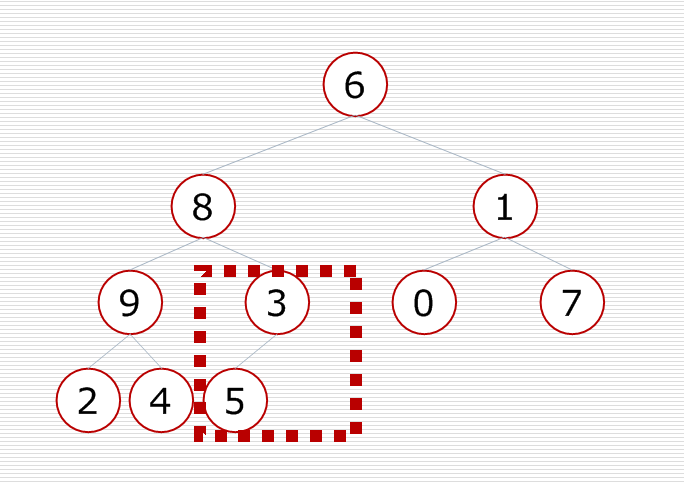
先調整最後一個小子樹,把大的元素放到這個小子樹的頂部,使小子樹變成一個堆

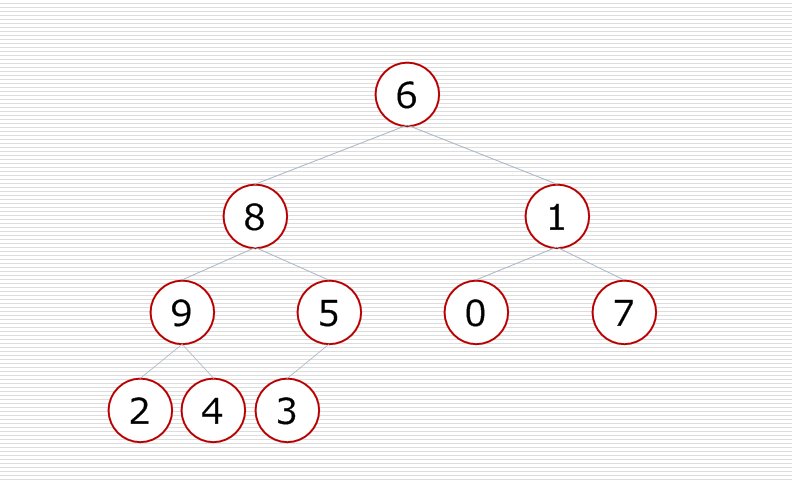
再對倒數第二個小子樹進行調整,使這個小子樹變成一個堆

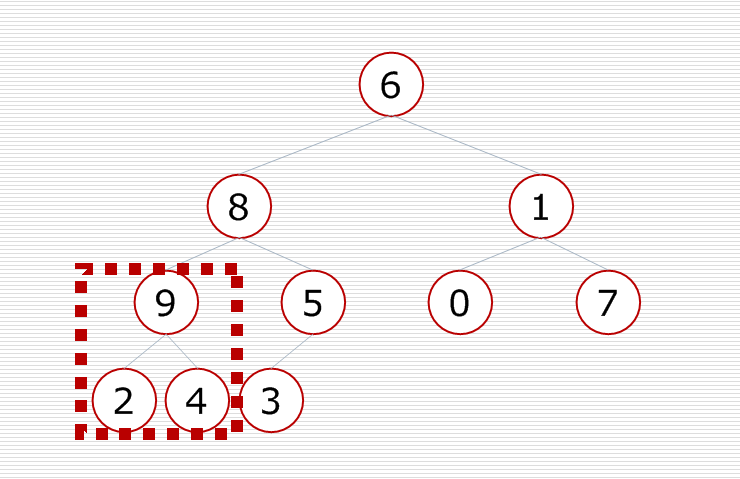
再對倒數第三個小子樹進行調整,使這個小子樹變成一個堆

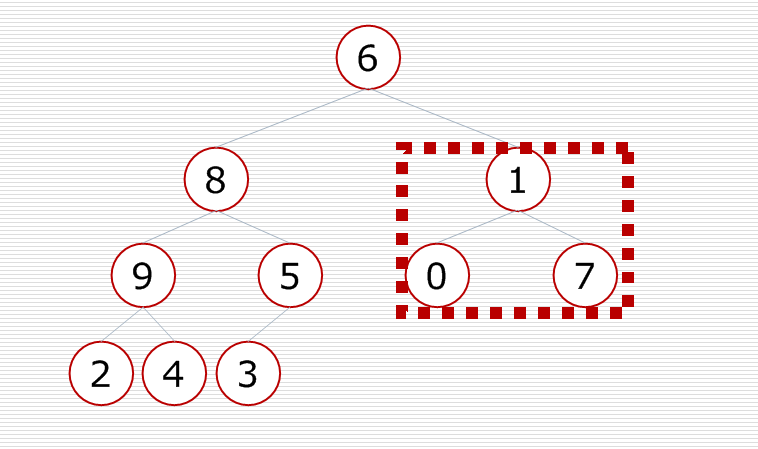
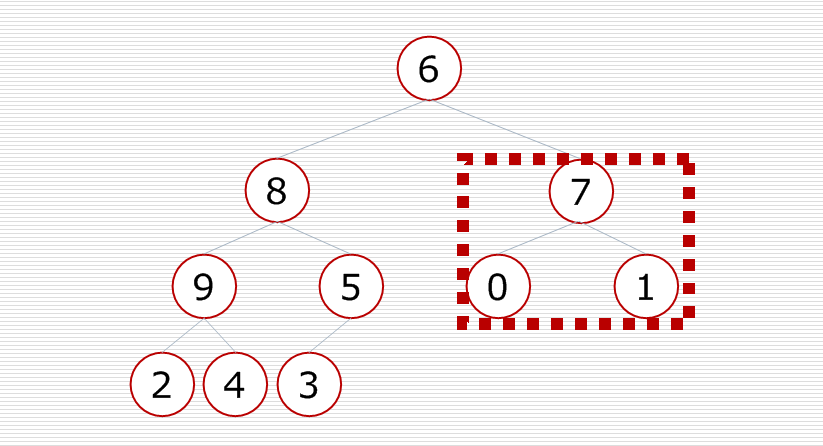
對這棵樹中的每一個小子樹都進行調整,最後這棵二叉樹就變成了一個大根堆.

堆排序過程:

1.建立堆
2.得到堆頂元素,為最大元素
3.去掉堆頂,將堆最後一個元素放到堆頂,此時可通過一次調整重新使堆有序
4.這時堆頂元素為堆中的第二大元素
5.重復3步驟,直到堆變空

代碼實現:

def sift(li,left,right):
    i=left
    j= 2 *i +1
    tmp=li[left]

    while j <=right:
        if j < right and li[j] < li[j+1]:
            j += 1

        if tmp < li[j]:
            li[i] = li[j]
            i  = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp

def heap_sort(li):
    n = len(li)

    for i in range(n//2-1 , -1 ,-1):
        sift(li,i,n-1)
        print(li)

    for j in range(n-1,-1,-1):
        li[0],li[j]=li[j],li[0]
        sift(li,0,j-1)
        print(li)

li=[2,9,7,8,5,0,1,6,4,3]

sift(li,0,len(li)-1)

heap_sort(li)
print(li)

輸出打印為:

[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[9, 8, 7, 6, 5, 0, 1, 2, 4, 3]
[8, 6, 7, 4, 5, 0, 1, 2, 3, 9]
[7, 6, 3, 4, 5, 0, 1, 2, 8, 9]
[6, 5, 3, 4, 2, 0, 1, 7, 8, 9]
[5, 4, 3, 1, 2, 0, 6, 7, 8, 9]
[4, 2, 3, 1, 0, 5, 6, 7, 8, 9]
[3, 2, 0, 1, 4, 5, 6, 7, 8, 9]
[2, 1, 0, 3, 4, 5, 6, 7, 8, 9]
[1, 0, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

歸並排序

把兩段有序列表合並成一個有序列表

例如現在有列表li=[2,5,7,8,9,1,3,4,6]

1.這個列表以9為分割線,將列表分為兩個部分,左邊的部分[2,5,7,8,9]是一個有序列表,右邊部分[1,3,4,6]也是一個有序列表
2.分別取這兩段有序列表中的第一個元素,分別是2和1,由於1比2小,所以先把1排入一個新列表tmp中
3.再取右邊部分的第二個元素3,3比2大,把2排入tmp中1元素的右邊
4.再取左邊部分的第二個元素5,5比3大,把3排入tmp中2元素右邊
5.再取右男家部分的第三個元素4,再對4進行排序
6.直到這兩段有序列表中的元素都排入tmp中,這時tmp就是li的有序狀態

代碼:

def merge(li, left, mid, right):
    i = left
    j = mid + 1

    ltmp = []

    while i <= mid and j <= right:
        if li[i] <= li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1

    while i <= mid:
        ltmp.append(li[i])
        i += 1

    while j <= right:
        ltmp.append(li[j])
        j += 1

    li[left:right + 1] = ltmp

def mergesort(li, left, right):
    if left < right:
        mid = (left + right) // 2
        mergesort(li, left, mid)
        mergesort(li, mid + 1, right)
        print(li[left:right + 1])

        merge(li, left, mid, right)
        print(li[left:right + 1])

li = [10, 4, 6, 3, 8, 2, 5, 7, 1, 9]

mergesort(li, 0, len(li) - 1)

print(li)

輸出打印:

[10, 4]
[4, 10]
[4, 10, 6]
[4, 6, 10]
[3, 8]
[3, 8]
[4, 6, 10, 3, 8]
[3, 4, 6, 8, 10]
[2, 5]
[2, 5]
[2, 5, 7]
[2, 5, 7]
[1, 9]
[1, 9]
[2, 5, 7, 1, 9]
[1, 2, 5, 7, 9]
[3, 4, 6, 8, 10, 1, 2, 5, 7, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

歸並排序將列表越分越小,直至分成一個元素,
一個元素是有序的
將兩個有序列表歸並,列表越來越大.

希爾排序

希樂排序是一種分組插入的排序算法

希爾排序每趟並不使某些元素有序,而是使整體數據越來越接近有序

最後一次排序使得所有的數據有序

希爾排序代碼:

def shell_sort(li):
    gap=len(li) //2
    while gap > 0:
        for i in range(gap,len(li)):
            tmp = li[i]
            j = i - gap
            while j >=0 and tmp < li[j]:

                li[j + gap] = li[j]
                j -=gap
            li[j + gap] = tmp
            print(li)
            
        gap /= 2
        
li=[10,4,6,3,8,2,5,7,1,9]

shell_sort(li)

print(li)

輸出打印:

[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 3, 8, 10, 5, 7, 1, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 4, 6, 1, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 6, 4, 8, 10, 5, 7, 3, 9]
[2, 1, 5, 4, 6, 10, 8, 7, 3, 9]
[2, 1, 5, 4, 6, 7, 8, 10, 3, 9]
[2, 1, 3, 4, 5, 7, 6, 10, 8, 9]
[2, 1, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 7, 6, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 9, 8, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

排序算法之NB三人組