前言

文本挖掘也是機器學習或者說是人工智能最需要處理的一類信息（其它的諸如語音、圖像及視頻處理等）；隨著數字信息化和網絡化進程不斷深入，用戶的在線交流、發布、共享等都被以文字形式記錄下來，它們成為分析語言和理解社會的重要素材來源，對於文本的挖掘主要包括文檔分類、信息提取、文檔聚類、主題建模等。

早期的文本處理主要偏向於依賴規則（依據語法規則生成相關語法樹），但這類方法偏向靜態，無法實時處理浩如煙海的互聯網及其它來源的文字素材，更為重要的是它無法體現各種語言之間的相關性，而在上世紀80年代開始，機器學習方法被大量地運用到自然語言的處理上來（主要是基於統計學方法，被稱為統計語言模型），實踐表明這類方法比基於規則的方式更為可靠，而且更為適應各類變化。

文本挖掘事宜計算語言學、數理統計分析為理論基礎，結合機器學習及信息檢索技術，從文本素材中提取或發現相關知識，其所使用的手段不外乎文本切割、特征抽取、數據降維等。

本文所涉及的文本挖掘技術主要包含文本的向量空間模型（主要針對TFIDF算法，即Term Frequency-Inverse Document Frequency，詞頻-倒排文檔頻）、LDA（Latent Dirichlet Allocation潛在狄利克雷分配）以及Google的Word2Vec等通用方法。

文本向量空間模型

如何實現將文本數據結構化是文本挖掘的核心問題，這個問題又被稱作文本的特征表示。向量空間模型是目前最為簡便高效的文本表示模型之一，它的基本思想就是將單詞從文檔中提取出來，每個單詞給予一定的權重；為了簡化分析，一般不考慮單詞在文檔中的先後順序（但單詞不能重復），這時可以把這些單詞所組成的東西看成是空間中的一個向量，而文檔與文檔之間的差異就可以使用余弦夾角的大小來判斷。如果特征只有單詞組成，而忽略其先後順序，則這種方式被稱作詞袋模式（

而TFIDF就是一種常用的統計加權技術，它用來評估一個詞對於一個文檔的重要性以及這個詞在一堆文檔（文集）中的重要性；換言之，如果一個詞在一個文檔中出現的頻次很高（這個就是所謂的TF，即詞頻），而且在文集中出現的頻次較低（這個就是所謂的IDF，即反向文檔頻率），則可以認為這個詞的識別度較高，可以用它來標識一個文檔而區分其它的文檔，形式化的，其計算公式如下：

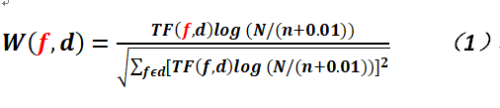
在上式中，f就是文本集特征，的是文檔，而TF(f,d)是詞頻，即特征詞在文本中出現的頻率，它的定義如下：

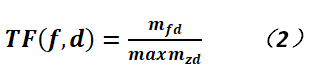
對於上式而言，mfd是f（特征詞）在文檔d中出現的次數，z是d中所有的特征詞；對於倒排文檔頻而言，它就是度量特征詞在文集中出現的頻繁成都，用於降低那些在語料（Corpus）過於頻繁出現的詞的重要程度，主要是它們對於文檔沒有什麽區分的能力，其計算公式如下：

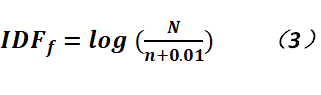
LDA模型

傳統的基於文本向量空間的模型，由於其維度太高（通常可能達到上萬維），而且因為強調了權值，而忽略了術語之間的關系，從而導致所謂的“維度災難”，故需將部分詞的權值轉化為更高層次的權值，這樣可以彌補僅以詞為特征的缺陷，這樣在一定程度上也降低了維度；而所謂的主題（Topic）可以充當這一角色，它包含了若幹個詞。

Latent Dirichlet Allocation模型是一種典型的用於提取主題的概率潛語義模型，它是由Blei等人提出的，它是一種具有文本主題表示能力的非指導學習模型。

在LDA模型的符號系統中使用w來表示詞，它是一個N維單位向量，我們依然使用d來表示文檔，這兩個概念和之前的基於向量空間模型沒有太大區別，而使用z來表示主題，一個單詞可以對應一個主題，一篇文檔則由幾個主題混合而成，記為{z1,z2,...,zN}，它也是一個單位向量；文檔語料（Corpus）集是M篇文檔的集合，記為D={w1,w2,...,wM}。

LDA模型其建模過程就是一個文檔的生成過程，生成模型是指模型可以隨機生成一些可觀測數據；LDA可以隨機生成一篇由一個到多個主題組成的文檔，其過程大致如下：

1. 以一定概率在若幹主題中選取主題；

2. 以一定概率在選中的主題中抽取詞語；

3. 不斷地重復上述步驟，直到生成一篇長度為N的文檔。

如果以形式化的方式來表示，為如下公式所示：

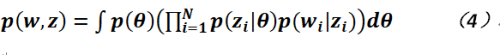
在上式當中，就是根據參數獲取主題的概率，而則是在一定主題之下獲取詞語的概率。那LDA模型和狄利克雷分布究竟有什麽關系？或者說這個模型為什麽要使用狄利克雷來命名？其原因在於Blei等人研究發現如果生成多篇文檔，則主題的分布也應該遵照一定的經驗概率模型，在這個模型中就是狄利克雷分布；我們知道狄利克雷分布被稱作分布的分布，就是可以用它來生成其它分布（其實主要是多項分布）的參數，故從這個角度而言，公式4可以寫為如下形式（參數的分布為Dir()）：

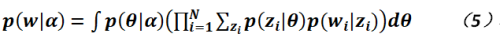
故綜上所述，LDA模型的基本思想就是將每個文檔表示為潛在主題的隨機混合模型，而每個主題標識為一系列詞語的概率分布。

具體到生成一篇文檔而言，其步驟如下：

1. 從泊松分布中隨機抽取N（文檔的長度）；

2. 選取從狄利克雷分布中生成參數，它是一個k維隨機向量（回憶下狄利克雷分布的形式即可知），它表示文檔中k個主題發生之概率，k固定為已知量；

3. 對於生成文檔中每一個詞語而言，先根據多項式分布（參數已由上步生成）選取主題，然後在給定主題下選擇詞語，其概率為，其中為在給定主題下的多項分布，參數是一個k*N的矩陣，，它代表主題i下生成單詞j的概率。

故LDA模型的聯合概率如以下公式所示：

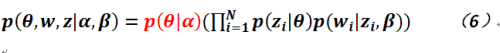
使用LDA模型對文本建模，就是要估計參數和，前者反映了主題模型的性質，而後者則反映了詞語在給定主題下的性質，但其實利用極大似然法是很難求解這兩個參數的，可以在EM算法（這個算法也是所謂機器學習的“十大算法”，其主要思想是在無法對目標函數直接求導數時，轉而利用Jenson不等式，求其下界函數的導數，然後不斷擡高下界而達到逼近目標函數的作用）中結合變分推斷來估計它們。

Word2Vec方法

從這個方法的名稱來看就可知它主要的目的是將詞轉換為向量，這個和文本向量空間模型是完全不同的，因為後者是將文章中的多個詞轉化為向量，這裏需要註意差別。將詞轉化為向量有個最為普通的方法，即令有長度為m的字典（這裏註意字典和語料的區別，語料是可以包含有重復單詞的），其對應詞的維度值為1，而其它維度的值只能為0，即這個向量就是所謂的One-hot向量，顯然這種方法會造成數據的過於稀疏，而且各個詞向量之間沒有任何關系，它們之間是正交的，即，故這種表示方法雖然簡單，但實際上沒有什麽太大的價值。

而Google的Word2Vec方法另辟蹊徑，利用單詞在上下文中的關系，對其進行向量化而取得了非常不錯的效果，甚至在自然語言互譯中也有很大作用（因為類似的單詞在向量空間上的距離較近），在介紹這個方法的文章中，《Word2Vec中的數學原理詳解》是非常不錯的一篇博文，值得仔細研讀，但其中對於為什麽要使用Hierarchical Softmax（層級式的Softmax）作為網絡的輸出其實並沒有特別地進行說明，這造成在讀這篇文章之初以為是必須要使用這種方法（一開始筆者也是這麽認為的），有的網友認為是基於縮減計算量的需要，我也認為確實如此，但相關文章中也沒有提到其根本原因，故在這篇文章中進行一定的說明，其實也可以不用基於層級的Softmax方法作為最終輸出，但這可以讓我們認識到，對於一個具有海量輸出的神經網絡而言，使用層級式的Softmax效果要優於一般的Softmax，這個對於手寫漢字的識別或人臉識別可能也是如此，因為漢字的輸出不會就那麽若幹個字母及數字。

本文無意於過多討論和描述Word2Vec的原理，因為相關文檔已經描述的極為清楚了，但考慮到完整性，還是會引用一些《Word2Vec中的數學原理詳解》內容；另外，文章最後一節講述到了這個方法的一些實現細節，其中有關於算法加速部分，這個倒是可以為廣大程序員所參考，但在談到對於指數函數求值的部分時，文章指出考慮到算法實現速度，會將指數函數使用泰勒公式展開，並且采用查表法獲取相應的值，筆者在這裏表示不太認同這種做法（不知原算法實現人員是基於什麽平臺開發的），因為筆者也在早期的實踐中也使用這種方式來求取指數函數的函數值，但發現其實和直接使用libm中的數學庫沒有存在什麽速度上的明顯差異（基於CPU時鐘數進行衡量），這裏的原因主要有兩點，其一是數學庫中已經使用了相關優化方法，其二是計算的速度不僅取決於算法的優化，主要還有Cache的命中情況（對於早期的CPU，程序員可能需要顯式地對數據進行預取，即利用prefetch指令，而新一代的處理器在這方面做得已經足夠智能了）。

Word2Vec主要包含兩個主要方法，其一是所謂的CBOW模型，而其二則是所謂的Skip-gram模型，它們之間存在一種互補的關系，另外還有一種基於負采樣的訓練。

前文提到Word2Vec並非采用傳統的Softmax作為輸出，而是使用Hierarchical Softmax，其主要表現形式就是哈夫曼數（Huffman Tree），這種數主要用於編碼上，主要特點是首先它是一個二叉樹（當然不是一般意義的二叉搜索樹、排序樹或平衡樹，如AVL或紅黑樹等常見二叉樹；這種樹是數據結構中較為基礎的一種，可以參看相關教科書），其次頻率越高的單詞其結點所在位置越靠近樹根，而其所謂的編碼就長度越短，從而可以從下面的相關推導可以看出，計算量越小，這就是為什麽要采用這種有些奇怪的輸出結構的原因，但總體還是保持了歸一化的特性；而這顆異常龐大（因為單詞很多）的哈夫曼樹的葉子節點都是單詞，非葉子節點包含了需要求解的參數向量，對於這些參數向量以及單詞向量的最大化的目標函數就是求解的根本目的。考慮到方便起見，默認樹的左子樹編碼為0，右子樹編碼為1，至於是否則需要去除單詞中的所謂Stop Words（比如中文的“的”，英文的“of”等頻率很高，但又沒有實際意義的詞），那就可能需要根據實際情況來處理。

CBOW

現令單詞的向量（使用x表示之）和參數（使用θ表示之）向量都是m維的實向量，則，假定對於某個單詞w，其前後各考察c（c一般可能不宜過大）個單詞，則共有2c個單詞，則對於每一次單獨訓練（當然其上下文不會只有2c個單詞，故針對每一次而言，只取一種上下文場景）而言，需將這些單詞的向量進行累加（就是簡單的向量加法；在訓練最初始，可以隨機生成這些單詞向量），生成一個向量，它被記作Xw；在其中還會使用Sigmoid函數來計算相關概率，那麽對於CBOW模型而言，其目標函數就是：

對於上式而言，在實際操作中，就是把詞向量和的變化率累加，再平均分攤到每個詞向量上，其中w‘是w的上下文。

Skip-gram

以上是對於CBOW（根據中間單詞求上下文單詞向量）模式的相關公式推導，而對於Skip-gram（根據上下文求中間單詞向量）模式而言，其實比較類似，其目標函數如下：

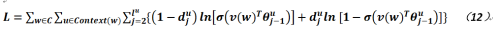
可以看出其形式與公式7較為類似，所不同的就是中間多了一層對於單詞w上下文的求和（這個很好理解，因為這是多個單詞求一個單詞的向量），另外就是Sigmoid函數的參數略有不同而已（其實還是一樣）。

那麽有了目標函數，則也能得到最終的參數更新公式（這個中間的步驟就不再重復了，讀者可以參考相關文檔，或者自行推導，其過程並不繁復），如下：

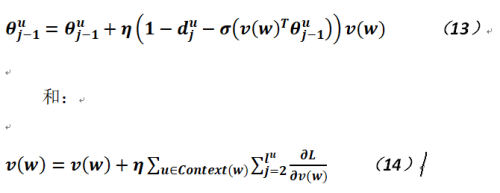
負采樣

以上就是對於兩個主要模型的相關比較簡略的推導，而負采樣又是什麽呢？因為在分類模型中，據研究表明如果給出了正例，而且還給出負例則能提高模型的識別度，故在Word2Vec中也實現了所謂的負采樣，在CBOW的負采樣中即最大化如下目標函數：

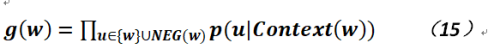
NEG(w)就是w的負例集合，我們希望對於正例而言則概率越大越好，而負例則越小越好，於是目標函數就是：

對於Skip-gram的負采樣，十分類似，不再贅述，可參考相關文檔。

其它

最後簡單地討論下如果輸出層不使用Hierarchical Softmax，而用一般的Softmax，則計算量為什麽會非常巨大。假定網絡輸入采用m個神經元（當然也可以使用2c*m個神經元，即不將輸入向量相加，但處理起來稍有些麻煩），也不使用隱層（顯然也可以使用，但計算量又更是巨大，而且效果不彰），輸出神經元就是語料集合的大小，它們之間沒有層次的關系，輸入和輸出之間為全連接，這時就可以將需要優化的參數θ看作是神經元之間連接的權重，網絡中共有m*|C|條連接，則相關目標函數就轉變成如下形式（紅色部分是為了區分w的含義不同）：

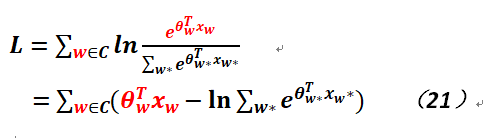
顯然，對於上式而言，由於Softmax公式的需要，必須基於全局的計算概率（相對而言，采用層次式的Softmax就不需要每次都遍歷全局，這裏就是巧妙處之所在，唯一需要付出的可能就是左右子樹的指針開銷，但若能采用整型索引進行存儲，可以減少一定的內存使用），而且因為這些參數在叠代的過程中會產生不停地變化，無法復用，所以計算量十分巨大。

關於機器學習中文本處理的一些常用方法