鄰接矩陣實現

例圖

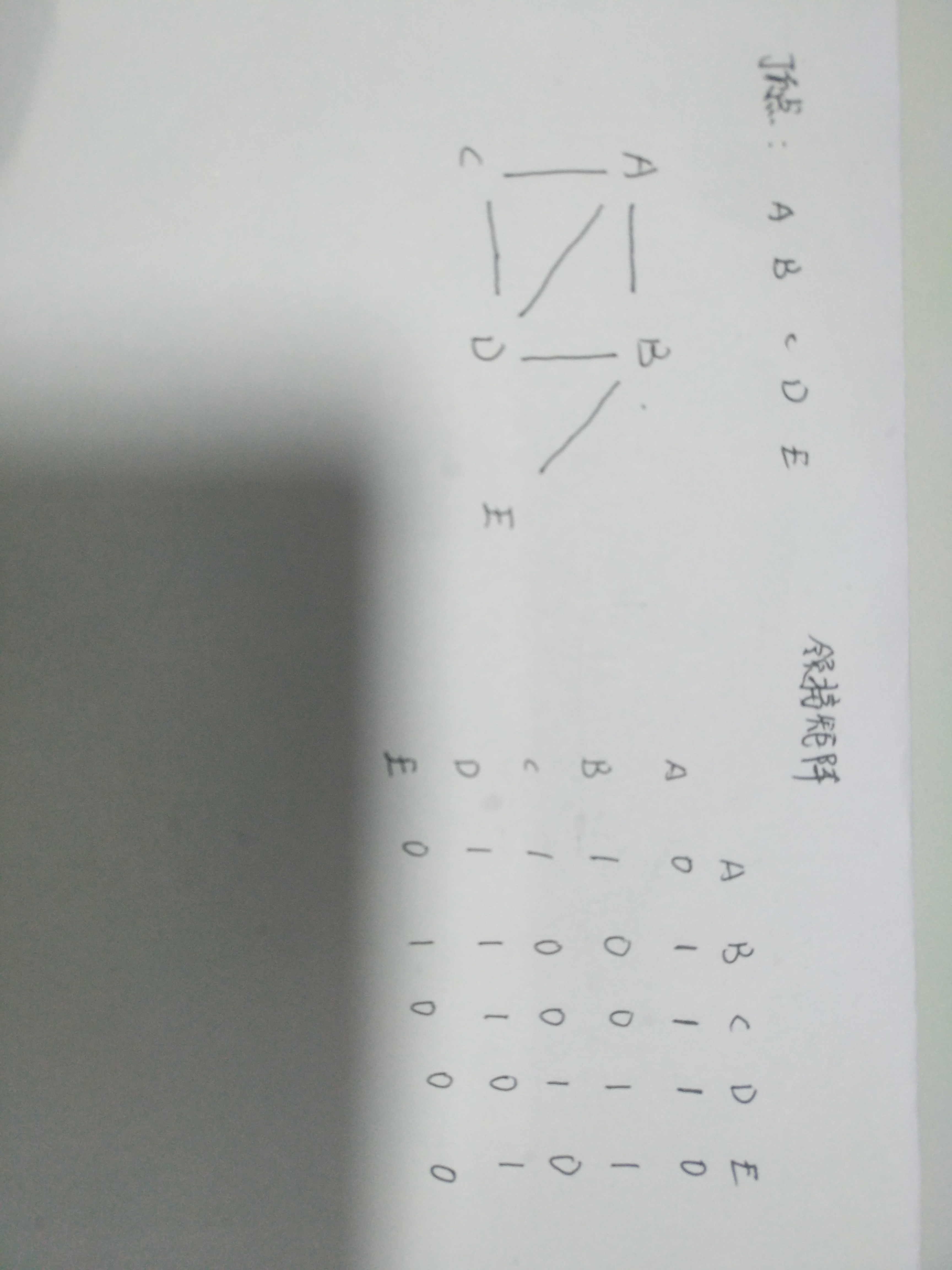
分析

變量

• 需要一個鏈表來保存數據-即保存結點
• 需要一個二維數組來保存每個變得權值，有則填入具體數值，沒有則用0
• 定義一個保存邊個數的值

函數方法

• 得到圖中邊的個數
• 得到結點的數據
• 得到具體邊的權值
• 插入結點，刪除節點
• 插入邊，刪除邊
• isEmpty，size
• 廣度優先遍歷，深度優先遍歷

具體實踐

• 插入,刪除結點與邊
  我認為鄰接矩陣的變換是根據結點來變化的。所以我先定義了構造函數它傳入參數n,作為初始值，用來幫助實例化結點鏈表和二維數組。

  public AMgroup (int n){
      edges = new int [n][n];
      myList = new ArrayList<>(n);
      NumEdges = 0;
      room = n;
  }
   
  

  插入結點並不改變二維數組本身，除非插入的結點個數大於初始參數n;但刪除結點時就不得不考慮由於結點remove導致二維數組中該節點參與的橫和列都不能填入值，0也不可以，應該移除此橫和列，重新定義新的數組。

  public void helpRemoveEdges(T item){
      int position = myList.indexOf(item);
      int[][] Newedge = new int[room-1][room-1];
      for (int i=0;i<room;i++){
          if (i==position){
              continue;
          }
          if (i<position){
              for (int j=0;j<room;j++){
                  if (j==position)
                      continue;
                  if (j<position)
                      Newedge[i][j]=edges[i][j];
                  if (j>position)
                      Newedge[i][j-1]=edges[i][j];
              }
          }
          if (i>position){
              for (int j=0;j<room;j++){
                  if (j==position)
                      continue;
                  if (j<position)
                      Newedge[i-1][j]=edges[i][j];
                  if (j>position)
                      Newedge[i-1][j-1]=edges[i][j];
              }
          }
      }
      edges = Newedge;
  }
   
  

• 插入刪除的具體代碼

  public void insertEdge(int x,int y,int weight){
      edges[x][y]=weight;
      NumEdges++;
  }
  public void removeEdge(int x,int y){
      edges[x][y]=0;
      NumEdges--;
  }
  public void insertNode(T item){
      myList.add(item);
  }
  public void removeNode(T item){
      helpRemoveEdges(item);
      myList.remove(item);
  }
   
  

• 深度優先遍歷

  1.訪問初始結點v，並標記結點v為已訪問。
  2.查找結點v的第一個鄰接結點w。
  3.若w存在，則繼續執行4，否則算法結束。
  4.若w未被訪問，對w進行深度優先遍歷遞歸（即把w當做另一個v，然後進行步驟123）。
  5.查找結點v的w鄰接結點的下一個鄰接結點，轉到步驟3

王彪-20162321《程序設計與數據結構2nd》-第十一周學習總結與實驗報告