[翻譯]基於詞典序的生成下一排列算法
翻譯來源https://www.nayuki.io/page/next-lexicographical-permutation-algorithm
簡介
假設對於一個有限長度的數組序列(0, 3, 3, 5, 8),需要生成對應的所有全排列。有什麽好的辦法做到?
最原始的方案是使用自頂向下的遞歸方式。首先選舉出第一個位置的元素,然後遞歸選擇第二個元素從剩下的元素中,直到剩余一個元素。但是這種方法很復雜因為它需要遞歸、堆棧存儲和去重。而且,如果堅持操作序列(不使用臨時數組),那麽這種方法在生成字典序排列的使用會有很大的困難。
最有效生成所有排列的方式是以字典序最小的開始,重復進行計算下一個排列。這個簡單而又快速的算法將在本頁進行闡述。我們將會使用具體的例子來解釋算法的每一個步驟。
算法描述
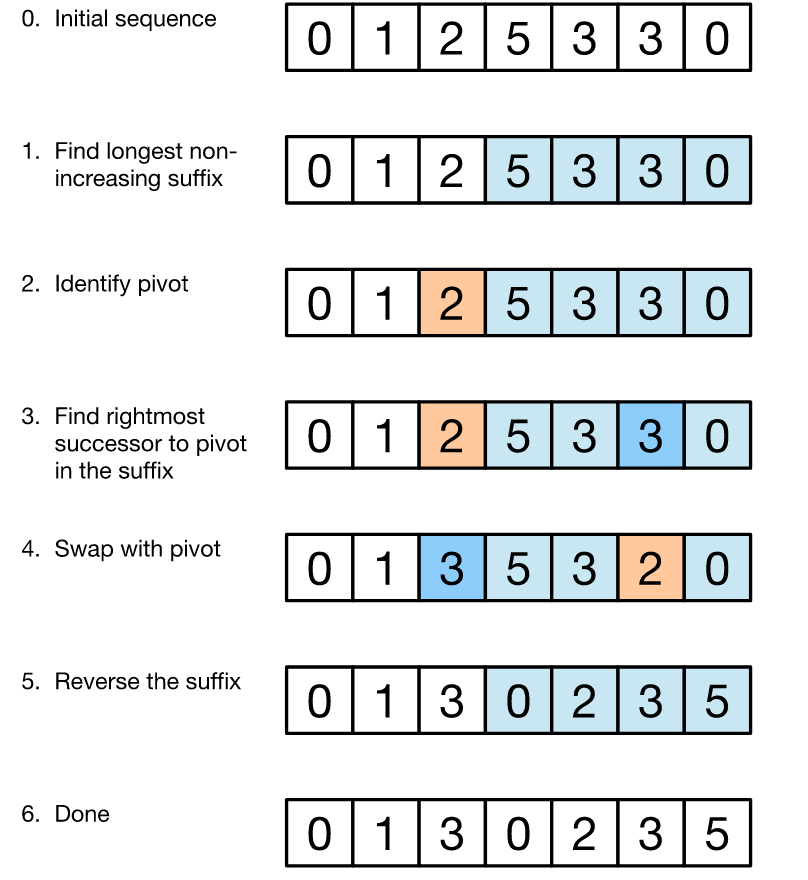
序列(0, 1, 2, 5, 3, 3, 0)作為測試數據。
本算法的關鍵步驟是當我們計算生成下一個排列時,必須盡可能小的增加序列值。就像我們數數一樣,我們總是盡可能的去修改最右側(低位)的數據,保持左側(高位)的數字不動一樣。例如:從{0,1}到{0,2},完全不需要將第一個元素從0改到1,改動第二個元素將獲得更小的增加。事實上,第二個元素也無需改動,這將是接下來要說明的。
首先,標記出最長的非升序後綴子串(微弱下降)。在例子中這個後綴子串就是(5, 3, 3, 0)。最長非升序後綴已經是後綴串所有排列中的最大排列了,所以不可能計算它的下一個組合,如果要獲得下一個組合,就必須和左側的元素作出交換。(標記最大非升序後綴字串可以在通過從右往左搜索在O(n)時間內完成,還有後綴至少含有一個元素,因為一個元素的子串是非升序的)。
第二步,取出後綴子串左側緊鄰的元素(本例子中是2)稱之為pivot。(如果沒有這個元素,那就說明整個字串是非升序的,那麽這個字符串就是最大的子串了)。pivot 必須小於後綴子串的第一個元素(5),故後綴中存在部分元素大於pivot.當我們把pivot和後綴中的大於pivot的最小元素進行交換後,就得到了最小的目標前綴。(前綴就是序列中去掉後綴的部分)。在這個例子中,最終得到了前綴(0, 1, 3)和更新後的後綴(5, 3, 2, 0)。(如果後綴有多個可選項,那就要選擇最右側的選項,接下來進入下一步。)
最後,對後綴進行非降序排序,因為前一步已經增大了前綴,所有我們希望後綴盡可能的小。事實上,完全可以避免排序而是進行簡單的倒置後綴,原因在於替換元素沒有改變排序。這樣就得到了序列(0, 1, 3, 0, 2, 3, 5)就是我們想要計算出的的下一個排列。
簡明的數學描述:
找出最大的索引i 確保有array[i ? 1] < array[i](如果不存在i,那說明序列已經是最大排列)
找出最大索引 j 使得 j ≥ i 同時 array[j] > array[i ? 1]。
交換array[j] 和 array[i ? 1]。
倒置以array[i]開頭的後綴子串。
如果你真的讀懂了這個算法,這裏還有一個拓展練習:設計一個算法計算出前一個最大的字典序排列。
樣例代碼 (Java)
boolean nextPermutation(int[] array) {
// Find longest non-increasing suffix
int i = array.length - 1;
while (i > 0 && array[i - 1] >= array[i])
i--;
// Now i is the head index of the suffix
// Are we at the last permutation already?
if (i <= 0)
return false;
// Let array[i - 1] be the pivot
// Find rightmost element that exceeds the pivot
int j = array.length - 1;
while (array[j] <= array[i - 1])
j--;
// Now the value array[j] will become the new pivot
// Assertion: j >= i
// Swap the pivot with j
int temp = array[i - 1];
array[i - 1] = array[j];
array[j] = temp;
// Reverse the suffix
j = array.length - 1;
while (i < j) {
temp = array[i];
array[i] = array[j];
array[j] = temp;
i++;
j--;
}
// Successfully computed the next permutation
return true;
}這個代碼可以按照你的理解機械翻譯為其他的編程語言。(註意:在Java中,數組從0開始)。
再次聲明翻譯https://www.nayuki.io/page/next-lexicographical-permutation-algorithm
龍城飛將,歡迎關註公眾號 可樂小數據[xiaokele_data]

[翻譯]基於詞典序的生成下一排列算法
