Codeforces 903D Almost Difference

Let‘s denote a function

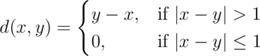
You are given an array a consisting of n integers. You have to calculate the sum of d(a_i,?a_j) over all pairs (i,?j) such that 1?≤?i

The first line contains one integer n (1?≤?n?≤?200000) — the number of elements in a.

The second line contains n integers a₁, a₂, ..., a_n (1?≤?a_i?≤?10⁹) — elements of the array.

Print one integer — the sum of d(a_i,?a_j) over all pairs (i,?j) such that 1?≤?i?≤?j?≤?n.

5
1 2 3 1 3

4

4
6 6 5 5

0

4
6 6 4 4

-8

In the first example:

1. d(a₁,?a₂)?=?0;
2. d(a₁,?a₃)?=?2;
3. d(a₁,?a₄)?=?0;
4. d(a₁,?a₅)?=?2;
5. d(a₂,?a₃)?=?0;
6. d(a₂,?a₄)?=?0;
7. d(a₂,?a₅)?=?0;
8. d(a₃,?a₄)?=??-?2;
9. d(a₃,?a₅)?=?0;
10. d(a₄,?a₅)?=?2.

分析：剛拿到這題，先想到的是：歸並排序，仔細構思了一下感覺細節很多，不大好寫；轉而去想線段樹（歸並排序能解決的線段樹都行），絕對值差在1及以內的直接不考慮就行了，那麽對於一個值x，要考慮的區間範圍是[1,x-2]U[x+2,+inf]，這樣先離散化，然後線段樹維護離散化後的下標，維護的信息有兩個：區間和與區間計數（sum和cnt），因為對於x的查詢結果sum和cnt，ans=cnt*x-sum，然後就是基本的單點更新，區間查詢了。這道題要用高精度，我偷懶沒寫。主要原因是這道題其實用不著線段樹，只要set或者map維護一下集合，然後維護前綴和即可。。這樣寫主程序代碼長度不超過50行，比我100行的線段樹代碼清爽多了。

代碼

Codeforces 903D Almost Difference