這節課介紹了斯坦納樹問題（Steiner tree）與旅行商問題（TSP），並講解了它們的近似算法。

平面上的斯坦納樹

平面上的斯坦納樹指的是這樣的問題：平面上有 $n$ 個點，要用總長盡量少的線段把它們連通起來。要註意，線段不一定要在給定的 $n$ 個點相交（不然跑個最小生成樹就沒了），完全可以在平面上的其它點相交。最優解中，線段在平面上除了給定點外的交點稱為斯坦納點。

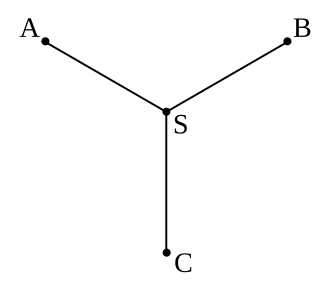
可以從上圖看出 $n = 3$ 和 $n = 4$ 的情況，$S$、$S_1$ 和 $S_2$ 是斯坦納點。$n = 3$ 時，斯坦納點就是三角形的費馬點。

平面上的斯坦納樹是一個 NP-Hard 問題。

滿足三角不等式的完全圖上的斯坦納樹

滿足三角不等式的完全圖上的斯坦納樹指的是這樣的問題：給定一張滿足三角不等式（對於任意兩兩有連邊的三點 $x, y, z$，有 $w(x, y) \le w(x, z) + w(z, y)$，$w$ 表示邊權）的完全圖 $G = (V, E)$ 和 $S \subseteq V$，求 $G$ 的連通子圖 $G‘$，使得 $S$ 中的所有點都在 $G‘$ 中，且 $G‘$ 邊權之和最小。

即使有了這麽多的限制條件，這個問題仍然是一個 NP-Hard 問題（證明見此）。下面我們提出它的一個 2- 近似算法：其實很簡單，只要算出 $S$ 的最小生成樹即可（別忘了是完全圖，$S$ 肯定是連通的）。

算法近似比證明：

假設最優的斯坦納樹邊權之和為 $\text{OPT}$，最小生成樹的邊權之和為 $\text{MST}$。我們把最優斯坦納樹中的每條邊復制一次，得到一張有歐拉回路的圖，它的邊權總和為 $2\text{OPT}$。

我們在歐拉圖中任選一個 $S$ 中的點出發，找到一條歐拉回路 $L$。我們只走 $S$ 中的點，且每個點只走一次，如果不能沿著 $L$ 走到下一個點就直接“跳到”那個點（別忘了是完全圖，這種“跳躍”稱為 short-cutting）。

舉個例子，例如上圖是我們找到的歐拉回路的一部分，紅色點是 $S$ 中的點。由於不能從第一個 a 沿著 $L$ 走到 $b$，我們要跳過去；由於 a 已經走過了，所以不能走 c → a → d，而是要從 c 直接跳到 d。

由於完全圖符合三角不等式，直接跳過去肯定不比沿著 $L$ 走過去來得長。這樣，我們就找到了 $S$ 的一個連通圖，而且這個連通圖的邊權之和至多為 $2\text{OPT}$。

別忘了，$S$ 的任何連通圖，邊權之和都不比最小生成樹小。所以我們有 $\text{MST} \le 2\text{OPT}$。這就證明了算法的近似比是 2。

用上圖的例子說明這個近似比對於這個算法是緊的。圖中沒有畫出來的邊權值都是 2。令 $S = \{1, 2, \dots, n\}$，顯然最優解為 $n$（利用中間的 0 作為斯坦納點），但用上面的算法會得到 $2(n-1)$ 的結果，在 $n$ 足夠大的時候近似比趨近於 2。

旅行商問題的近似比

大家都知道，完全圖上的 TSP 是 NP-Hard。然而，完全圖上的 TSP 甚至沒有很好的近似比。下面證明完全圖上的 TSP 不存在近似比為 $O(2^{\text{poly}(n)})$ 的多項式算法，其中 $\text{poly}(n)$ 表示 $n$ 的多項式。

我們利用哈密爾頓回路問題進行證明。對於普通無向圖 $G = (V, E)$ 上的哈密爾頓回路問題，我們構造完全圖 $G‘ = (V, E‘)$，$E‘$ 中一條邊 $e‘$ 的邊權 $w(e‘)$ 定義如下：$$w(e‘) = \begin{cases} 1 & e‘ \in E \\ 2^{\text{poly}(n)}n & e‘ \not\in E \end{cases}$$ 這張完全圖的輸入規模仍然是 $n$ 的多項式。

如果 TSP 存在近似比為 $O(2^{\text{poly}(n)})$ 的算法，那麽對於上面的完全圖，算法就絕對不能選 $e‘ \not\in E$ 的邊。但如果算法只用 $e‘ \in E$ 的邊構造出了一個解，那就同時找到了 $G$ 中的哈密爾頓回路。我們知道，找哈密爾頓回路本身就是 NPC 的，這就完成了證明。

滿足三角不等式的完全圖的旅行商問題

既然普通完全圖上的旅行商問題這麽難，我們給它加一點限制。在滿足三角不等式的完全圖上，TSP 就有很好的近似比。

首先容易證明這個問題近似比上界為 2：先跑個最小生成樹（邊權和肯定小等於最優哈密爾頓回路），把樹上每條邊重復一次變成歐拉圖，在歐拉圖上進行和斯坦納樹類似的 short-cutting 即可。

不過我們可以證明一個更緊的上界。不一定要把樹上每條邊都重復一次才能得到歐拉圖嘛，如果我們把樹上度數為奇數的點（下面簡稱奇點）進行配對（一張圖的奇點肯定有偶數個，不用擔心有一個匹配不上），每一對之間連一條邊，那麽構成的圖就都是偶點，也就是一張歐拉圖了。這種配對工作非常容易，只要用帶花樹什麽的求一個最小權完美匹配即可。下面證明這種算法的近似比為 1.5。

假設最優的哈密爾頓回路如上圖，白色的點是最小生成樹上的奇點。我們將奇點按順序進行 short-cutting，就能得到兩個不相交匹配（1 - 2, 3 - 4, ..., 2k-1 - 2k 以及 2 - 3, 4 - 5, ..., 2k - 1）。由於滿足三角不等式，這兩個匹配的權值之和肯定不大於 $\text{OPT}$，那麽兩個匹配中較小的那個權值肯定不大於 $0.5\text{OPT}$。別忘了，我們在算法中求出來的可是最小完美匹配，那麽最小完美匹配的權值肯定也不大於 $0.5\text{OPT}$。最小生成樹 + 最小權完美匹配就證明了 1.5 的近似比。

上面的例子可以說明 1.5 對這個算法是緊的，沒有畫出來的邊權值都是 2。右邊實線是算法可能獲得的最小生成樹，虛線是算法可能算出的最小權完美匹配。顯然最優解為 $n$，而算法可能得出的解是 $n + \frac{n}{2}$。只要“梯形”上面的點足夠多，那麽近似比就是 1.5。

滿足三角不等式的完全圖的最短哈密爾頓路

下面來考慮一個有些不一樣的問題：在滿足三角不等式的完全圖中，給定 $k = \{0, 1, 2\}$ 個固定點（即指定起點或者終點，或者都指定，或者都不指定），求滿足固定點的最短哈密爾頓路。

這個問題可以通過以下近似算法解決：

1. 首先求個最小生成樹 $T$；

2. 令點集 $S$ 包含兩類點：在最小生成樹上是偶點的固定點（因為要把固定點變奇點，才好找以它們開頭的歐拉路），以及在最小生成樹上是奇點的非固定點；

3. 類似於 TSP 問題，求個 $S$ 的最小權匹配 $M$，要求有 $2-k$ 個非固定點不匹配（只要加入 $2-k$ 個輔助點，與非固定點連權值為 0 的輔助邊即可）。容易發現，這樣會恰有 2 個點成為奇點，並且固定點一定在這 2 個點裏；

4. 這樣 $T \cup M$ 就是一張有歐拉路的圖，用 short-cutting 的方法把歐拉路變成哈密爾頓路即可。

這個算法在 $k \in \{0, 1\}$ 時是 1.5 近似算法。下面進行證明。

$k = 0$

證明思想與 TSP 類似。假設最優解上有 $2t$ 個奇點，那麽可以拆成兩個匹配：1 - 2, 3 - 4, ..., (2t-3) - (2t-2)（2t-1 和 2t 沒有匹配） 與 2 - 3, 4 - 5, 6 - 7, ..., (2t-2) - (2t-1)（1 和 2t 沒有匹配），就可以證明 $M$ 的權值之和至多為 $0.5\text{OPT}$。

$k = 1$

不妨設起點（設為 s）是固定點。

如果起點是奇點比較好辦，假設最優解上有 $2t+1$ 個奇點（不含起點），那麽可以拆成兩個匹配：1 - 2, 3 - 4, ..., (2t-1) - 2t（2t+1 沒有匹配）與 2 - 3, 4 - 5, ..., 2t - (2t+1)（1 沒有匹配）；

如果起點是偶點就比較麻煩了。假設最優解上有 $2t$ 個奇點，因為起點必須被匹配，我們沒法把最優解拆成兩個匹配符合要求的匹配。不過我們可以先把最優解拆成兩個匹配 $M_1$：s - 1, 2 - 3, ..., (2t-2) - (2t-1)（2t 沒有匹配），以及 $M_2$：1 - 2, 3 - 4, ..., (2t-1) - 2t（s 沒有匹配）。

記 $w(M)$ 表示匹配 $M$ 的權重之和。如果 $w(M_1) < w(M_2)$ 那把 $M_1$ 並入 $T$ 答案就已經出來了，否則我們用 $T \cup M_2$ 得到一張歐拉圖，找出一條哈密爾頓回路，再去掉連接 s 的一條邊，獲得以 s 為起點的哈密爾頓路。由於 $w(M_2) \le w(M_1)$，而我們加進圖的是 $M_2$，所以仍然有 1.5 的近似比。

$k = 2$

$k = 2$ 的情況稍有不同，這個算法在同時給定起點與終點的情況下，近似比為 5/3。這次我們要把 $T \cup \text{OPT}$ 拆成 3 個匹配來完成證明。下面以起點（記為 s）與終點（記為 t）均為偶點為例進行證明，其它情況類似。

不難發現，$T - \{s, t\}$ 中有偶數個點，那麽 $S$ 中也有偶數個點。設最優路徑依次經過 $s, v_1, v_2, \dots, v_{2k}, t$，其中 $v_i$ 是 $T$ 上的奇度點。

記 $u - v$ 表示僅通過最優路徑中的邊從點 $u$ 走到點 $v$，$u \sim v$ 表示僅通過 $T$ 中的邊從點 $u$ 走到點 $v$。我們嘗試將 $T \cup \text{OPT}$ 拆成這樣三個部分（不一定是匹配），且每條邊至多使用一次：
1. $s - v_1, v_2 - v_3, \dots, v_{2k-2} - v_{2k-1}, v_{2k} - t$；
2. $v_1 - v_2, v_3 - v_4, \dots, v_{2k-1} - v_{2k}, s \sim t$；
3. 找到 $s, t, v_1, v_2, \dots, v_{2k}$ 的一個排列 $u_1, u_2, \dots, u_{2k+2}$，$u_1 \sim u_2, u_3 \sim u_4, \dots, u_{2k+1} \sim u_{2k+2}$。

由於三角不等式，$u \sim v$ 所使用的邊的權值總和，一定大等於直接連接 $u$ 和 $v$ 的邊的權值。如果我們能找到以上拆分，且每條邊至多使用一次，那麽我們就找到了 3 個 $S$ 的完美匹配，其權值總和不超過 $2\text{OPT}$。這樣，$S$ 的最小權完美匹配權值就不會超過 $\frac{2}{3}\text{OPT}$，就能證明 $\frac{5}{3}$ 的近似比。

舉個例子。左圖中，實線是 $T$ 的邊，虛線是 $\text{OPT}$ 中的邊；紅邊是部分 1 中的邊，藍邊是部分 2 中的邊，綠邊是部分 3 中的邊。

再看右圖。雖然所有綠色邊不能構成一個匹配，但是橙色邊卻可以構成一個匹配，而且權值之和一定不大於綠色邊的權值之和。

很顯然，部分 1 與部分 2 中除開 $s \sim t$ 之外的邊，就組成了最優路徑。我們通過以下算法，在 $T$ 上找到部分 3 以及部分 2 中 $s \sim t$ 中的邊：

1. 在 $T$ 中找到從 $s$ 到 $t$ 的路徑作為 $s \sim t$，去掉使用過的邊；
2. 對於每個連通塊，選擇任意一個奇度點 $u$，在 $T$ 中找到通往另一個奇度點 $v$ 的路徑，且路徑上不含其它奇度點。去掉使用過的邊；
3. 重復步驟 2，直到 $S$ 中的點都在步驟 2 中找到了對應的點。

根據算法描述容易看出，如果算法成功退出，我們就找到了需要的拆分。接下來說明 $S$ 中的每個點都能在步驟 2 中找到對應的點，即算法可以成功退出。

註意到 $s$ 與 $t$ 均為偶度點。步驟 1 結束後，由於 $s$ 與 $t$ 是路徑端點，去掉路徑上的邊後，$s$ 與 $t$ 都變成了奇度點；而路徑上的其它點在去掉路徑上的邊後，奇偶性不變。

步驟 2 中，由於每個連通塊一定有偶數個奇度點，所以一定可以找到符合要求的 $u$ 和 $v$。由於路徑中間不含其它奇度點，所以其它點的奇偶性不變，不影響算法的後續運行；而 $u$ 與 $v$ 作為路徑端點，在去掉路徑中的邊後都變成了偶度點，不會再次被選中，也不影響算法的後續運行。

因此，我們一定可以將 $T \cup \text{OPT}$ 拆成 $S$ 的 3 個完美匹配，即可證明算法的近似比不超過 $\frac{5}{3}$。

應用運籌學基礎：組合優化 (6) - 近似算法選講 (4)