區間DP

題目描述

丁丁最近沈迷於一個數字遊戲之中。這個遊戲看似簡單，但丁丁在研究了許多天之後卻發覺原來在簡單的規則下想要贏得這個遊戲並不那麽容易。遊戲是這樣的，在你面前有一圈整數（一共n個），你要按順序將其分為m個部分，各部分內的數字相加，相加所得的m個結果對10取模後再相乘，最終得到一個數k。遊戲的要求是使你所得的k最大或者最小。

例如，對於下面這圈數字（n=4，m=2）：

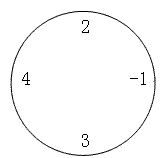
要求最小值時，((2-1) mod 10)×((4+3) mod 10)=1×7=7，要求最大值時，為((2+4+3) mod 10)×(-1 mod 10)=9×9=81。特別值得註意的是，無論是負數還是正數，對10取模的結果均為非負值。

丁丁請你編寫程序幫他贏得這個遊戲。

輸入輸出格式

輸入格式：

輸入文件第一行有兩個整數，n（1≤n≤50）和m（1≤m≤9）。以下n行每行有個整數，其絕對值不大於104，按順序給出圈中的數字，首尾相接。

輸出格式：

輸出文件有兩行，各包含一個非負整數。第一行是你程序得到的最小值，第二行是最大值。

自己不好好玩遊戲還要叫人幫忙寫程序

大體思路就這樣，展開成2n的鏈再區間內DP。轉移方程是f[i][j][m] = max(f[i][j-1][m-1]*s[j][j], f[i][k][m-1]*s[k+1][j])，最小值同理。

那麽時間復雜度是，還是可以接受的。實測洛谷5個點60ms。

不過這題呢坑點如下：

1.這個取模很有趣

2.最小值的g數組初始化有點意思。雖然數據範圍不大，但是如果極端情況n=50,m=9,{ai}=104的話也是會出事的。好在數據非常人性，於是我用著奇奇怪怪的判別方法硬是初始化了過去。

這麽快都2018年的寒假了，一年前這個時候都快開學了吧……

寒假切的第一題祭。

（怎麽感覺這題都做了這麽久……）

數字遊戲&寒假祭