java中排序算法
Java中排序可以分為內部排序,外部排序具體如下:

這裏我們討論選擇排序、冒泡排序、快速排序
選擇排序
在要排序的一組數中,選出最小(或者最大)的一個數與第1個位置的數交換;然後在剩下的數當中再找最小(或者最大)的與第2個位置的數交換,依次類推,直到第n-1個元素(倒數第二個數)和第n個元素(最後一個數)比較為止。

操作方法:
第一趟,從n 個記錄中找出關鍵碼最小的記錄與第一個記錄交換;
第二趟,從第二個記錄開始的n-1 個記錄中再選出關鍵碼最小的記錄與第二個記錄交換;
以此類推.....
第i 趟,則從第i 個記錄開始的n-i+1 個記錄中選出關鍵碼最小的記錄與第i 個記錄交換,
直到整個序列按關鍵碼有序。
package com;
public class SimpleSelectSort {
public static void main(String[] args) {
int a[] = {3,1,5,7,2,4,9,6,10,8};
SimpleSelectSort obj=new SimpleSelectSort();
System.out.println("初始值:");
obj.print(a);
obj.selectSort(a);
System.out.println("\n排序後:");
obj.print(a);
}
private void selectSort(int[] a) {
for(int i=0;i<a.length;i++){
int k=i;//k存放最小值下標。每次循環最小值下標+1
for(int j=i+1;j<a.length;j++){//找到最小值下標
if(a[k]>a[j])
k=j;
}
swap(a,k,i);//把最小值放到它該放的位置上
}
}
public void print(int a[]){
for(int i=0;i<a.length;i++){
System.out.print(a[i]+" ");
}
}
public void swap(int[] data, int i, int j) {
if (i == j) {
return;
}
data[i] = data[i] + data[j];
data[j] = data[i] - data[j];
data[i] = data[i] - data[j];
}
}簡單選擇排序改進
簡單選擇排序,每趟循環只能確定一個元素排序後的定位。我們可以考慮改進為每趟循環確定兩個元素(當前趟最大和最小記錄)的位置,從而減少排序所需的循環次數。改進後對n個數據進行排序,最多只需進行[n/2]趟循環即可。具體實現如下:
冒泡排序
基本思想:
在要排序的一組數中,對當前還未排好序的範圍內的全部數,自上而下對相鄰的兩個數依次進行比較和調整,讓較大的數往下沈,較小的往上冒。即:每當兩相鄰的數比較後發現它們的排序與排序要求相反時,就將它們互換。
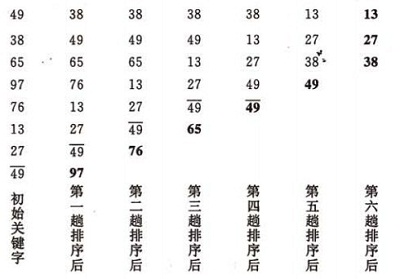
冒泡排序的示例:
void bubbleSort(int a[], int n){
for(int i =0 ; i< n-1; ++i) {
for(int j = 0; j < n-i-1; ++j) {
if(a[j] > a[j+1])
{
int tmp = a[j] ; a[j] = a[j+1] ; a[j+1] = tmp;
}
}
}
}
冒泡排序算法的改進
對冒泡排序常見的改進方法是加入一標誌性變量exchange,用於標誌某一趟排序過程中是否有數據交換,如果進行某一趟排序時並沒有進行數據交換,則說明數據已經按要求排列好,可立即結束排序,避免不必要的比較過程。本文再提供以下兩種改進算法:
1.設置一標誌性變量pos,用於記錄每趟排序中最後一次進行交換的位置。由於pos位置之後的記錄均已交換到位,故在進行下一趟排序時只要掃描到pos位置即可。
改進後算法如下:
void Bubble_1 ( int r[], int n) {
int i= n -1; //初始時,最後位置保持不變
while ( i> 0) {
int pos= 0; //每趟開始時,無記錄交換
for (int j= 0; j< i; j++)
if (r[j]> r[j+1]) {
pos= j; //記錄交換的位置
int tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
i= pos; //為下一趟排序作準備
}
}
2.傳統冒泡排序中每一趟排序操作只能找到一個最大值或最小值,我們考慮利用在每趟排序中進行正向和反向兩遍冒泡的方法一次可以得到兩個最終值(最大者和最小者) , 從而使排序趟數幾乎減少了一半。
改進後的算法實現為:
void Bubble_2 ( int r[], int n){
int low = 0;
int high= n -1; //設置變量的初始值
int tmp,j;
while (low < high) {
for (j= low; j< high; ++j) //正向冒泡,找到最大者
if (r[j]> r[j+1]) {
tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
--high; //修改high值, 前移一位
for ( j=high; j>low; --j) //反向冒泡,找到最小者
if (r[j]<r[j-1]) {
tmp = r[j]; r[j]=r[j-1];r[j-1]=tmp;
}
++low; //修改low值,後移一位
}
}
快速排序
基本思想:
1)選擇一個基準元素,通常選擇第一個元素或者最後一個元素,
2)通過一趟排序講待排序的記錄分割成獨立的兩部分,其中一部分記錄的元素值均比基準元素值小。另一部分記錄的 元素值比基準值大。
3)此時基準元素在其排好序後的正確位置
4)然後分別對這兩部分記錄用同樣的方法繼續進行排序,直到整個序列有序。
快速排序的示例:
(a)一趟排序的過程:

(b)排序的全過程

算法的實現:
遞歸實現:
package com;
public class QuickSort {
public static void main(String[] args) {
int a[] = {3,1,5,7,2,4,9,6,10,8};
QuickSort obj=new QuickSort();
System.out.println("初始值:");
obj.print(a);
int h=a.length-1;
obj.quickSort(a,0,h);
System.out.println("\n排序後:");
obj.print(a);
}
private void quickSort(int[] a,int low, int high) {
if(low<high){ //如果不加這個判斷遞歸會無法退出導致堆棧溢出異常
int middle=getMiddle(a,low,high);
quickSort(a, 0, middle-1); //遞歸對低子表遞歸排序
quickSort(a, middle + 1, high); //遞歸對高子表遞歸排序
}
}
public int getMiddle(int[] a, int low, int high){
int key = a[low];//基準元素,排序中會空出來一個位置
while(low<high){
while(low<high && a[high]>=key){//從high開始找比基準小的,與low換位置
high--;
}
a[low]=a[high];
while(low<high && a[low]<=key){//從low開始找比基準大,放到之前high空出來的位置上
low++;
}
a[high]=a[low];
}
a[low]=key;//此時low=high 是基準元素的位置,也是空出來的那個位置
return low;
}
public void print(int a[]){
for(int i=0;i<a.length;i++){
System.out.print(a[i]+" ");
}
}
}
分析:
快速排序是通常被認為在同數量級(O(nlog2n))的排序方法中平均性能最好的。但若初始序列按關鍵碼有序或基本有序時,快排序反而蛻化為冒泡排序。為改進之,通常以“三者取中法”來選取基準記錄,即將排序區間的兩個端點與中點三個記錄關鍵碼居中的調整為支點記錄。快速排序是一個不穩定的排序方法。
快速排序的改進
在本改進算法中,只對長度大於k的子序列遞歸調用快速排序,讓原序列基本有序,然後再對整個基本有序序列用插入排序算法排序。實踐證明,改進後的算法時間復雜度有所降低,且當k取值為 8 左右時,改進算法的性能最佳。算法思想如下:
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基準元素
while(low < high){ //從表的兩端交替地向中間掃描
while(low < high && a[high] >= privotKey) --high; //從high 所指位置向前搜索,至多到low+1 位置。將比基準元素小的交換到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void qsort_improve(int r[ ],int low,int high, int k){
if( high -low > k ) { //長度大於k時遞歸, k為指定的數
int pivot = partition(r, low, high); // 調用的Partition算法保持不變
qsort_improve(r, low, pivot - 1,k);
qsort_improve(r, pivot + 1, high,k);
}
}
void quickSort(int r[], int n, int k){
qsort_improve(r,0,n,k);//先調用改進算法Qsort使之基本有序
//再用插入排序對基本有序序列排序
for(int i=1; i<=n;i ++){
int tmp = r[i];
int j=i-1;
while(tmp < r[j]){
r[j+1]=r[j]; j=j-1;
}
r[j+1] = tmp;
}
}
int main(){
int a[10] = {3,1,5,7,2,4,9,6,10,8};
cout<<"初始值:";
print(a,10);
quickSort(a,9,4);
cout<<"結果:";
print(a,10);
}
java中排序算法
