3月3日考試總結
title: 3月3日考試總結
data: 2018-3-3 20:18:40
tags:
- 線段樹
- 圖論
- 最短路
- Floyd
- 二分答案
- 倍增
- 貪心
description: 第一道題目是線段樹維護區間和區間平方和支持區間修改;第二道題目是用一條邊連接兩個聯通塊使得聯通塊的直徑最小;第三道題是二份答案加機智處理.
Luogu P1471 方差
題目背景
滾粗了的HansBug在收拾舊數學書,然而他發現了什麽奇妙的東西。
題目描述
蒟蒻HansBug在一本數學書裏面發現了一個神奇的數列,包含N個實數。他想算算這個數列的平均數和方差。
輸入輸出格式
輸入格式:
第一行包含兩個正整數N、M,分別表示數列中實數的個數和操作的個數。第二行包含N個實數,其中第i個實數表示數列的第i項。
- 操作1:1 x y k ,表示將第x到第y項每項加上k,k為一實數。
- 操作2:2 x y ,表示求出第x到第y項這一子數列的平均數。
- 操作3:3 x y ,表示求出第x到第y項這一子數列的方差。
輸出格式:
輸出包含若幹行,每行為一個實數,即依次為每一次操作2或操作3所得的結果(所有結果四舍五入保留4位小數)。
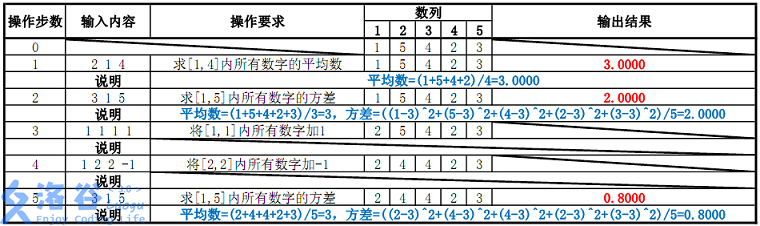
輸入輸出樣例
輸入樣例#1:
5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5
輸出樣例#1:
3.0000
2.0000
0.8000
說明

樣例說明:
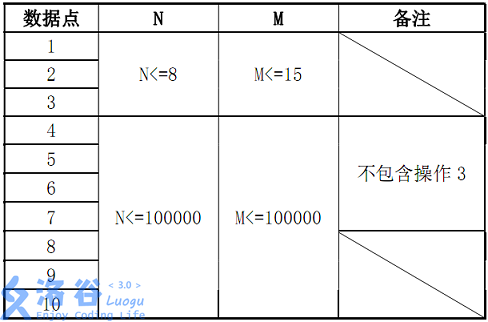
數據規模:
做法:
首先區間平均數是很容易維護的, 用線段樹或者分塊維護區間和除去區間大小就是區間平均數.區間加也是線段樹的常見操作.
\[ \begin{align} S^2=&\frac{1}{r-l+1}\sum_{i=l}^r|A_i-\bar{A}|^2\=&\frac{1}{r-l+1}\sum_{i=l}^r(A_i-\bar{A})^2\=&\frac{1}{r-l+1}(\sum_{i=l}^rA_i^2-2A_i\bar{A}+\bar{A}^2)\\end{align} \]
我們觀察到這個式子只和\(\sum\limits_{i=l}^rA_i^2,\sum\limits_{i=l}^rA_i,\bar{A}\)
還需要考慮在區間加下維護區間平方和的問題,仍然推公式.
\[ \begin{align} \sum_{i=l}^r(A_i+\Delta A)^2=&\sum_{i=l}^r(A_i^2+2A_i\Delta A+\Delta A^2)\\end{align} \]
Code
// luogu-judger-enable-o2
#include<algorithm>
#include<iostream>
#include<cstdio>
#define N 100005
using namespace std;
namespace Input{
inline void read(int &s){
char ch=getchar();int f=1;
for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(s=0;isdigit(ch);s=s*10+ch-'0',ch=getchar());
s*=f;
}
void read(double &s){
cin>>s;
}
};using namespace Input;
struct Node{
double data,flag,pingfang;
int l,r;
}t[N<<2];
double merge(int l,int r){
return t[l].data+t[r].data;
}
void pushdown(int ret){
if(!t[ret].flag)return ;
int l=t[ret].l,r=t[ret].r;
int mid=(l+r)>>1;
t[ret<<1].flag+=t[ret].flag;
t[ret<<1|1].flag+=t[ret].flag;
t[ret<<1].pingfang+=(mid-l+1)*t[ret].flag*t[ret].flag+2*t[ret<<1].data*t[ret].flag;
t[ret<<1].data+=(mid-l+1)*t[ret].flag;
t[ret<<1|1].pingfang+=(r-mid)*t[ret].flag*t[ret].flag+2*t[ret<<1|1].data*t[ret].flag;
t[ret<<1|1].data+=(r-mid)*t[ret].flag;
t[ret].flag=0;
}
void Build(int l,int r,int ret){
t[ret]=(Node){0.0,0.0,0.0,l,r};
if(l==r){
read(t[ret].data);
t[ret].pingfang=t[ret].data*t[ret].data;
return ;
}
int mid=(l+r)>>1;
Build(l,mid,ret<<1);
Build(mid+1,r,ret<<1|1);
t[ret].data=merge(ret<<1,ret<<1|1);
t[ret].pingfang=t[ret<<1].pingfang+t[ret<<1|1].pingfang;
}
void Addition(int L,int R,int ret,double delta){
int l=t[ret].l,r=t[ret].r;
if(l>=L&&r<=R){
t[ret].flag+=delta;
t[ret].pingfang+=(r-l+1)*delta*delta+2*t[ret].data*delta;
t[ret].data+=delta*(r-l+1);
return;
}
int mid=(l+r)>>1;
pushdown(ret);
if(L<=mid)Addition(L,R,ret<<1,delta);
if(R>mid)Addition(L,R,ret<<1|1,delta);
t[ret].data=merge(ret<<1,ret<<1|1);
t[ret].pingfang=t[ret<<1].pingfang+t[ret<<1|1].pingfang;
}
double Query(int L,int R,int ret){
int l=t[ret].l,r=t[ret].r;
if(l>=L&&r<=R)
return t[ret].data;
double ans=0;
pushdown(ret);
int mid=(l+r)>>1;
if(L<=mid)ans+=Query(L,R,ret<<1);
if(R>mid)ans+=Query(L,R,ret<<1|1);
return ans;
}
double QueryF(int L,int R,int ret){
int l=t[ret].l,r=t[ret].r;
if(l>=L&&r<=R)
return t[ret].pingfang;
double ans=0;
pushdown(ret);
int mid=(l+r)>>1;
if(L<=mid)ans+=QueryF(L,R,ret<<1);
if(R>mid)ans+=QueryF(L,R,ret<<1|1);
return ans;
}
double pingjunshu(int l,int r){
return (double)Query(l,r,1)/(double)(r-l+1);
}
double fangcha(int l,int r){
double sigma=Query(l,r,1);
double truepj=sigma/(r-l+1);
return (QueryF(l,r,1)-2*truepj*sigma+truepj*sigma)/(r-l+1);
}
int main(){
int n,m;
int apt;
int a,b;
double delta;
read(n);read(m);
Build(1,n,1);
for(int i=1;i<=m;++i){
read(apt);read(a);read(b);
if(apt==1){
read(delta);
Addition(a,b,1,delta);
}
else if(apt==2){
printf("%.4lf\n",pingjunshu(a,b));
}
else {
printf("%.4lf\n",fangcha(a,b));
}
}
return 0;
}Luogu P1522 牛的旅行 Cow Tours
題目描述
農民 John的農場裏有很多牧區。有的路徑連接一些特定的牧區。一片所有連通的牧區稱為一個牧場。但是就目前而言,你能看到至少有兩個牧區通過任何路徑都不連通。這樣,Farmer John就有多個牧場了。
John想在牧場裏添加一條路徑(註意,恰好一條)。對這條路徑有以下限制:
一個牧場的直徑就是牧場中最遠的兩個牧區的距離(本題中所提到的所有距離指的都是最短的距離)。考慮如下的有5個牧區的牧場,牧區用“*”表示,路徑用直線表示。每一個牧區都有自己的坐標:
(15,15) (20,15)
D E
*-------*
| _/|
| _/ |
| _/ |
|/ |
*--------*-------*
A B C
(10,10) (15,10) (20,10)【請將以上圖符復制到記事本中以求更好的觀看效果,下同】
這個牧場的直徑大約是12.07106, 最遠的兩個牧區是A和E,它們之間的最短路徑是A-B-E。
這裏是另一個牧場:
*F(30,15)
/
_/
_/
/
*------*
G H
(25,10) (30,10)在目前的情景中,他剛好有兩個牧場。John將會在兩個牧場中各選一個牧區,然後用一條路徑連起來,使得連通後這個新的更大的牧場有最小的直徑。
註意,如果兩條路徑中途相交,我們不認為它們是連通的。只有兩條路徑在同一個牧區相交,我們才認為它們是連通的。
輸入文件包括牧區、它們各自的坐標,還有一個如下的對稱鄰接矩陣:
A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0其他鄰接表中可能直接使用行列而不使用字母來表示每一個牧區。輸入數據中不包括牧區的名字。
輸入文件至少包括兩個不連通的牧區。
請編程找出一條連接兩個不同牧場的路徑,使得連上這條路徑後,這個更大的新牧場有最小的直徑。輸出在所有牧場中最小的可能的直徑。
輸入輸出格式
輸入格式:
第1行: 一個整數N (1 <= N <= 150), 表示牧區數
第2到N+1行: 每行兩個整數X,Y (0 <= X ,Y<= 100000), 表示N個牧區的坐標。註意每個 牧區的坐標都是不一樣的。
第N+2行到第2*N+1行: 每行包括N個數字(0或1) 表示如上文描述的對稱鄰接矩陣。
輸出格式:
只有一行,包括一個實數,表示所求直徑。數字保留六位小數。
只需要打到小數點後六位即可,不要做任何特別的四舍五入處理。
輸入輸出樣例
輸入樣例#1:
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010輸出樣例#1:
22.071068說明
翻譯來自NOCOW
USACO 2.4
做法:
要求在兩個任意聯通塊之間連上一條邊, 讓其直徑最短.所以就可以依次枚舉兩個聯通塊並枚舉它們的任意兩點連上一條邊,求出直徑更新答案即可.
要快速求出連邊之後聯通塊的直徑,只需要求出兩個聯通塊到達所連邊的點的最大距離即可, 註意直徑不一定通過所連接的邊,所以直徑可能會是某個其它聯通塊的直徑, 再加上連邊的長度就是直徑.至於如何求出到達一個點的最大距離, 用最短路處理即可,這裏用Floyd算法.
為什麽這樣做復雜度是正確的?我們觀察到枚舉連邊需要枚舉兩個聯通塊並枚舉其中的邊, 但是圖的總點數是\(n\leq 150\), 而不會枚舉一個點多次, 所以這一步的復雜度是\(O(n^2)\),Floyd的算法復雜度是\(O(n^3)0\), 在加上處理聯通塊的深搜\(O(n)\),總復雜度是\(O(n^3)\).
Code
// luogu-judger-enable-o2
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define N 155
using namespace std;
double dis[N][N];
int here[N][N];
int map[N][N];
int x[N],y[N];
double lon[N];
int color;
int be[N];
int n;
double distan(int i,int j){
if(i==j)return 0.000;
return sqrt((double)(x[i]-x[j])*(double)(x[i]-x[j])+(double)(y[i]-y[j])*(double)(y[i]-y[j]));
}
void dfs(int x,int c){
be[x]=c;here[c][++here[c][0]]=x;
for(int i=1;i<=n;++i)
if(!be[i]&&map[i][x])
dfs(i,c);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d%d",&x[i],&y[i]);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
char ch=getchar();
while(!isdigit(ch))ch=getchar();
map[i][j]=(ch=='1'?true:false);
if(map[i][j])dis[i][j]=distan(i,j);
else dis[i][j]=0x3f3f3f3f;
}
for(int i=1;i<=n;++i)
dis[i][i]=0;
for(int i=1;i<=n;++i)
if(!be[i])
dfs(i,++color);
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(dis[i][k]+dis[k][j]<dis[i][j])
dis[i][j]=dis[i][k]+dis[k][j];
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(dis[i][j]!=0x3f3f3f3f){
lon[i]=max(lon[i],dis[i][j]);
lon[j]=max(lon[j],dis[i][j]);
}
double ans=123456789000;
for(int i=1;i<=color;++i)
for(int j=1;j<=color;++j){
if(i==j)continue;
for(int k=1;k<=here[i][0];++k)
for(int l=1;l<=here[j][0];++l){
double o=0.0;
o=max(o,lon[here[i][k]]+lon[here[j][l]]+distan(here[j][l],here[i][k]));
if(o<ans)ans=o;
}
}
for(int i=1;i<=n;++i)
ans=max(ans,lon[i]);
printf("%.6f",ans);
return 0;
}Logu P1084 疫情控制
題目描述
H 國有 n 個城市,這 n 個城市用 n-1 條雙向道路相互連通構成一棵樹,1 號城市是首都,也是樹中的根節點。
H 國的首都爆發了一種危害性極高的傳染病。當局為了控制疫情,不讓疫情擴散到邊境城市(葉子節點所表示的城市),決定動用軍隊在一些城市建立檢查點,使得從首都到邊境城市的每一條路徑上都至少有一個檢查點,邊境城市也可以建立檢查點。但特別要註意的是,首都是不能建立檢查點的。
現在,在 H 國的一些城市中已經駐紮有軍隊,且一個城市可以駐紮多個軍隊。一支軍隊可以在有道路連接的城市間移動,並在除首都以外的任意一個城市建立檢查點,且只能在一個城市建立檢查點。一支軍隊經過一條道路從一個城市移動到另一個城市所需要的時間等於道路的長度(單位:小時)。
請問最少需要多少個小時才能控制疫情。註意:不同的軍隊可以同時移動。
輸入輸出格式
輸入格式:
第一行一個整數 n,表示城市個數。
接下來的 n-1 行,每行 3 個整數,u、v、w,每兩個整數之間用一個空格隔開,表示從城市 u 到城市 v 有一條長為 w 的道路。數據保證輸入的是一棵樹,且根節點編號為 1。
接下來一行一個整數 m,表示軍隊個數。
接下來一行 m 個整數,每兩個整數之間用一個空格隔開,分別表示這 m 個軍隊所駐紮的城市的編號。
輸出格式:
共一行,包含一個整數,表示控制疫情所需要的最少時間。如果無法控制疫情則輸出-1。
輸入輸出樣例
輸入樣例#1:
4
1 2 1
1 3 2
3 4 3
2
2 2
輸出樣例#1:
3
說明
【輸入輸出樣例說明】
第一支軍隊在 2 號點設立檢查點,第二支軍隊從 2 號點移動到 3 號點設立檢查點,所需時間為 3 個小時。
【數據範圍】
保證軍隊不會駐紮在首都。
對於 20%的數據,\(2≤ n≤ 10\);
對於 40%的數據,\(2 ≤n≤50,0<w <10^5\);
對於 60%的數據,\(2 ≤ n≤1000,0<w <10^6\);
對於 80%的數據,\(2 ≤ n≤10,000\);
對於 100%的數據,\(2≤m≤n≤50,000,0<w <10^9\)。
NOIP 2012 提高組 第二天 第三題
做法:
這道題相對來說是這三道題中最難的,但是一旦掌握了一些方法和技巧就能輕松解決此題.
首先要求所需時間最少, 我們可以聯想到二分答案, 二分所需時間, 只需要判斷時間內能不能滿足即可, 需要\(O(\log n)\)次判斷.
我們還知道, 因為結點是同步移動的, 而軍隊越往上走覆蓋的結點越多, 所以在不超過時間的情況下, 將結點盡可能的往上移動, 跳到根結點為止, 當然一個一個移動還是太慢了, 所以可以用倍增來加速.
在結點不能再跳躍時, 必定有一些結點還能再往其它根結點的子樹跳躍, 也必定有一些結點沒有被覆蓋, 所以我們利用這些還能跳躍的節點進行覆蓋, 根據顯然的貪心策略, 選出剩余時間最多的軍隊和距離根節點最遠的結點進行配對是最優的.
3月3日考試總結
