comm block orm src 基於 我們 技術分享 HR normal

一棵link/cut tree是一種用以表示一個森林，一個有根樹集合的數據結構。它提供以下操作：

• 向森林中加入一棵只有一個點的樹。
• 將一個點及其子樹從其所在的樹上斷開。
• 將一個點連接至另一個頂點，作為其子節點。
• 求出一個點所在樹的根。通過對兩個不同的點進行此操作，我們可以判斷他們是否屬於同一棵樹。
  翻譯自Link/cut tree - Wikipedia，英語好的小夥伴看這個就很不錯

在link/cut tree中，邊分為兩種：偏愛邊(preferred edges)和普通邊(normal edges)，每個非葉節點都有一條偏愛邊指向其偏愛子節點(preferred child)。偏愛邊形成的路徑稱為偏愛路徑(preferred paths)

。
實際上，link/cut tree是將森林劃分為若幹條鏈(也就是偏愛路徑)，並用以深度作為splay去分別維護每一條鏈。這些splay被稱為輔助樹(auxiliary tree)。操作時不要考慮splay的結構，只要考慮原樹的結構就好。
link/cut tree主要支持四種操作makeRt(p)、cut(p)、link(p,q)、path(p,q)，而這些操作都是基於access(p)的。下面分別介紹如何實現這些操作。

Access

void access(int p) {for(int q=0;p;q=p,p=fa[p]) splay(p),ch[p][1]=q,update(p);}

首先當然要介紹作為萬惡之源的access(p)

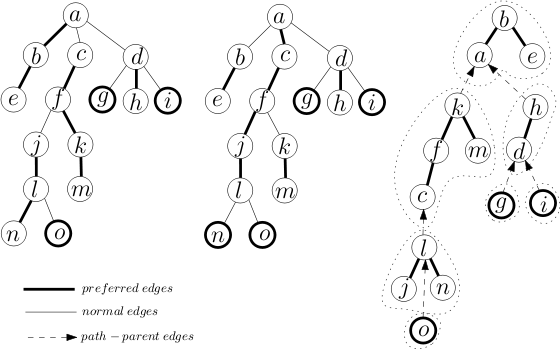
。access(p)的效果是將\(p\)與其所在樹的根置於一條鏈上，並且\(p\)是這條鏈的末尾。可以看一下wiki的這張圖：
左邊是access(l)前，中間是access(l)後，右邊是在splay上的實際操作。

實際操作中，我們要斷掉\(p\)下面的點，並將\(p\)所在鏈連接到它上面的一個點\(t\)上，然後斷掉\(t\)下面的點。大概是這樣：

每經過一次這樣的操作，\(p\)就會連接到上一層的鏈上。反復操作直到\(p\)與\(rt\)相連。
在輔助樹中，斷掉\(p\)下面的點相當於splay(p)並改變ch[p][1]。\(q\)記錄應該將誰接在\(t\)下面，也就是上一次的\(p\)啦。

MakeRt

void makeRt(int p) {access(p); splay(p),rever(p);}

rever(p)表示翻轉splay中的\(p\)。當我們access(p)後，\(p\)成為了其所在鏈上最深的點，那麽splay(p)後\(p\)就只有左子樹。翻轉\(p\)就把\(p\)變成了鏈上最淺的點，也就是根啦。
這段細節上我也想不太明白...別的點怎麽啦？

Cut

void cut(int p) {access(p); splay(p),fa[ch[p][0]]=0,ch[p][0]=0; update(p);}

斷掉\(p\)上面的點，也就是斷掉與ch[p][0]的連接。

Link

void link(int p,int q) {makeRt(p); fa[p]=q;}

如果\(p\)是一棵樹的根的話，直接將\(p\)接在\(q\)下面就可以了。

Path

void path(int p,int q) {makeRt(p),access(q),splay(q);}

將\(p\)變為根，再把\(q\)和根（也就是\(p\)）置於同一鏈上。這樣就形成了一個只維護\((p,q)\)這條鏈的輔助樹，然後就可以為所欲為啦。

Link/cut Tree