點擊標題下「異步社區」可快速關註

機器學習是解決很多文本任務的基本工具，本文自然會花不少篇幅來介紹機器學習。要想搞明白什麽是機器學習，一定要知道一些概率論和信息論的基本知識，本文就簡單回顧一下這些知識。

1.1　概率論

概率就是描述一個事件發生的可能性。我們生活中絕大多數事件都是不確定的，每一件事情的發生都有一定的概率（確定的事件就是其概率為100%而已）。天氣預報說明天有雨，那麽它也只是說明天下雨的概率很大。再比如擲骰子，我把一個骰子擲出去，問某一個面朝上的概率是多少？在骰子沒有做任何手腳的情況下，直覺告訴你任何一個面朝上的概率都是1/6，如果你只擲幾次，是很難得出這個結論的，但是如果你擲上1萬次或更多，那麽必然可以得出任何一個面朝上的概率都是1/6的結論。這就是大數定理：當試驗次數（樣本）足夠多的時候，事件出現的頻率無限接近於該事件真實發生的概率。

假如我們用概率函數來表示隨機變量x∈X的概率分布，那麽就要滿足如下兩個特性

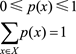
聯合概率p(x,y)表示兩個事件共同發生的概率。假如這兩個事件相互獨立，那麽就有聯合概率p(x,y) = p(x)p(y)。

條件概率p(y | x)是指在已知事件x發生的情況下，事件y發生的概率，且有p(y | x) = p(x,y)/p(x)。如果這兩個事件相互獨立，那麽p(y | x)與p(y)相等。

聯合概率和條件概率分別對應兩個模型：生成模型和判別模型。我們將在下一章中解釋這兩個模型。

概率分布的均值稱為期望，定義如下

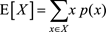
期望就是對每個可能的取值x，與其對應的概率值p(x)，進行相乘求和。假如一個隨機變量的概率分布是均勻分布，那麽它的期望就等於一個固定的值，因為它的概率分布p

概率分布的方差定義如下

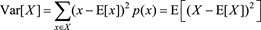
可以看出，方差是表示隨機變量偏離期望的大小，所以它是衡量數據的波動性的，方差越小表示數據越穩定，反之，方差越大表示數據的波動性越大。

另外，你還需要知道的幾個常用的概率分布：均勻分布、正態分布、二項分布、泊松分布、指數分布，等等。你還可以了解一下矩陣的知識，因為所有公式都可以表示成矩陣形式。

1.2　信息論

假如一個朋友告訴你外面下雨了，你也許覺得不怎麽新奇，因為下雨是很平常的一件事情，但是如果他告訴你他見到外星人了，那麽你就會覺得很好奇：真的嗎？外星人長什麽樣？同樣兩條信息，一條信息量很小，一條信息量很大，很有價值，那麽怎麽量化這個價值呢？這就需要信息熵，一個隨機變量X

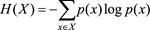
信息越少，事件（變量）的不確定性越大，它的信息熵也就越大，搞明白該事件所需要的額外信息就越多，也就是說搞清楚小概率事件所需要的額外信息較多，比如說，為什麽大多數人願意相信專家的話，因為專家在他專註的領域了解的知識（信息量）多，所以他對某事件的看法較透徹，不確定性就越小，那麽他所傳達出來的信息量就很大，聽眾搞明白該事件所需要的額外信息量就很小。總之，記住一句話：信息熵表示的是不確定性的度量。信息熵越大，不確定性越大。

聯合熵的定義為

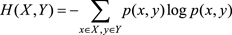
聯合熵描述的是一對隨機變量X和Y的不確定性。

條件熵的定義為

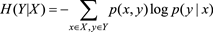
條件熵衡量的是：在一個隨機變量X已知的情況下，另一個隨機變量Y的不確定性。

相對熵（又叫KL距離，信息增益）的定義如下

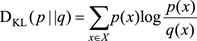
相對熵是衡量相同事件空間裏兩個概率分布（函數）的差異程度（而前面的熵衡量的是隨機變量的關系）。當兩個概率分布完全相同時，它們的相對熵就為0，當它們的差異增加時，相對熵就會增加。相對熵又叫KL距離，但是它不滿足距離定義的3個條件中的兩個：（1）非負性（滿足）；（2）對稱性（不滿足）；（3）三角不等式（不滿足）。它的物理意義就是如果用q分布來編碼p分布（一般就是真實分布）的話，平均每個基本事件編碼長度增加了多少比特。

兩個隨機變量X和Y，它們的互信息定義為

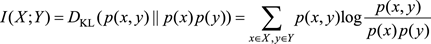
互信息是衡量兩個隨機變量的相關程度，當X和Y完全相關時，它們的互信息就是1；反之，當X和Y完全無關時，它們的互信息就是0。

對於x和y兩個具體的事件來說，可以用點互信息（Pointwise Mutual Information）來表示它們的相關程度。後面的章節就不做具體區分，都叫作互信息。

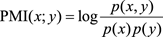
互信息和熵有如下關系

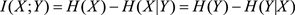
互信息和KL距離有如下關系

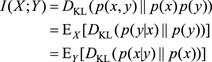
如果X和Y完全不相關，

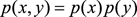
，則

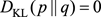
，互信息也為0。可以看出互信息是KL距離的期望。

交叉熵的定義如下

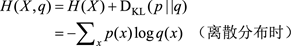
它其實就是用分布q來表示X的熵是多少，也就是說用分布q來編碼X（其完美分布是p）需要多付出多少比特。

好了，介紹了這麽多概念公式，那麽我們來個實際的例子，在文本處理中，有個很重要的數據就是詞的互信息。前面說了，互信息是衡量兩個隨機變量（事件）的相關程度，那麽詞的互信息，就是衡量兩個詞的相關程度，例如，“計算機”和“硬件”的互信息就比“計算機”和“杯子”的互信息要大，因為它們更相關。那麽如何在大量的語料下統計出詞與詞的互信息呢？公式中可以看到需要計算3個值：p(x)、p(y)和p(x,y)。它們分別表示x獨立出現的概率，y獨立出現的概率，x和y同時出現的概率。前兩個很容易計算，直接統計詞頻然後除以總詞數就知道了，最後一個也很容易，統計一下x和y同時出現（通常會限定一個窗口）的頻率，除以所有無序對的個數就可以了。這樣，詞的互信息就計算出來了，這種統計最適合使用Map-Reduce來計算。

1.3　貝葉斯法則

貝葉斯法則是概率論的一部分，之所以單獨拿出來介紹，是因為它真的很重要。它是托馬斯?貝葉斯生前在《機遇理論中一個問題的解》（An Essay Towards Solving a Problem in Doctrine of
Chance）中提出的一個當時叫“逆概率”問題。貝葉斯逝世後，由他的一個朋友替他發表了該論文，後來在這一理論基礎上，逐漸形成了貝葉斯學派。

貝葉斯法則的定義如下

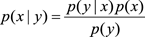
p(x | y)稱為後驗概率，p(y | x)稱為似然概率，p(x)稱為先驗概率，p(y)一般稱為標準化常量。也就是說，後驗概率可以用似然概率和先驗概率來表示。這個公式非常有用，很多模型以它為基礎，例如貝葉斯模型估計、機器翻譯、Query糾錯、搜索引擎等等。在後面的章節中，大家經常會看到這個公式。

好了，這個公式看著這麽簡單，到底能有多大作用呢？我們先拿中文分詞來說說這個公式如何應用的。

中文分詞在中文自然語言處理中可以算是最底層、最基本的一個技術了，因為幾乎所有的文本處理任務都要首先經過分詞這步操作，那麽到底要怎麽對一句話分詞呢？最簡單的方法就是查字典，如果這個詞在字典中出現了，那麽就是一個詞。當然，查字典要有一些策略，最常用的就是最大匹配法。最大匹配法是怎麽回事呢？舉個例子來說，要對“中國地圖”來分詞，先拿“中”去查字典，發現“中”在字典裏（單個詞肯定在字典裏），這時肯定不能返回，要接著查，“中國”也在字典裏，然後再查“中國地”，發現它沒在字典裏，那麽“中國”就是一個詞了；然後以同樣的方法處理剩下的句子。所以，最大匹配法就是匹配在字典中出現的最長的詞。查字典法有兩種：正向最大匹配法和反向最大匹配法，一個是從前向後匹配，一個是從後向前匹配。但是查字典法會遇到一個自然語言處理中很棘手的問題：歧義問題。如何解決歧義問題呢？

我們就以“學歷史知識”為例來說明，使用正向最大匹配法，我們把“學歷史知識”從頭到尾掃描匹配一遍，就被分成了“學歷\史\知識”，很顯然，這種分詞不是我們想要的結果；但是如果我們使用反向最大匹配法從尾到頭掃描匹配一遍，那就會分成“學/歷史/知識”，這才是我們想要的分詞結果。可以看出用查字典法來分詞，就會存在二義性，一種解決辦法就是分別從前到後和從後到前匹配。在這個例子中，我們分別從前到後和從後到前匹配後，將得到“學歷\史\知識”和“學/歷史/知識”，很顯然，這兩個分詞都有“知識”，那麽說明“知識”是正確的分詞，然後就看“學歷\史”和“學/歷史”哪個是正確的。從我們的角度看，很自然想到“學/歷史”是正確的，為什麽呢？因為（1）在“學歷\史”中“史”這個詞單獨出現的概率很小，在現實中我們幾乎不會單獨使用這個詞；（2）“學歷”和“史”同時出現的概率也要小於“學”和“歷史”同時出現的概率，所以“學/歷史”這種分詞將會勝出。這只是我們人類大腦的猜測，有什麽數學方法證明呢？有，那就是基於統計概率模型。

我們的數學模型表示如下：假設用戶輸入的句子用S表示，把S分詞後可能的結果表示為A：A1, A2,…, Ak（Ai表示詞），那麽我們就是求條件概率p(A | S)達到最大值的那個分詞結果。這個概率不好求出，這時貝葉斯法則就用上派場了，根據貝葉斯公式改寫為

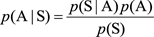
顯然，p(S)是一個常數，那麽公式相當於改寫成

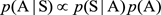
其中，p(S | A)表示(A)這種分詞生成句子S的可能性；p(A)表示(A)這種分詞本身的可能性。

下面的事情就很簡單了。對於每種分詞計算一下p(S | A)p(A)這個值，然後取最大的，得到的就是最靠譜的分詞結果。比如“學歷史知識”（用S表示）可以分為如下兩種（當然，實際情況就不止兩種情況了）：“學歷\史\知識”（用A表示，A1=學歷，A2=史，A3=知識）和“學/歷史/知識”（用B表示，B1=學，B2=歷史，B3=知識），那麽我們分別計算一下p(S | A)p(A)和p(S | B)p(B)，哪個大，就說明哪個是好的分詞結果。

但是

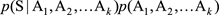
這個公式並不是很好計算，

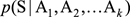
可以認為就是1，因為由

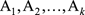
必然能生成S，那麽剩下的問題就是如何計算

。

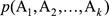
在數學中，要想簡化數學模型，就要利用假設。我們假設句子中一個詞的出現概率只依賴於它前面的那個詞（當然可以依賴於它前面的 m 個詞），這樣，根據全概率公式

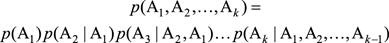
就可以改寫為

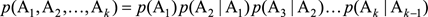
接下來的問題就是如何估計

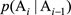
。然而，

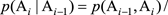
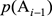
，這個問題變得很簡單，只要數一數（

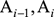
）這對詞在統計的文本中前後相鄰出現了多少次，以及Ai?1本身在同樣的文本中出現了多少次，然後用兩個數除以它就可以了。

上面計算

的過程其實就是統計語言模型，然而真正在計算語言模型的時候，要對公式進行平滑操作。Zipf定律指出：一個單詞出現的頻率與它在頻率表裏的排名（按頻率從大到小）成反比。這說明對於語言中的大多數詞，它們在語料中的出現是稀疏的，數據稀疏會導致所估計的分布不可靠，更嚴重的是會出現零概率問題，因為

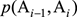
的值有可能為0，這樣整個公式的值就為0，而這種情況是很不公平的，所以平滑解決了這種零概率問題。具體的平滑算法讀者可以參考論文《An Empirical Study of Smoothing Techniques for Language Modeling》。

然而在實際系統中，由於性能等因素，很少使用語言模型來分詞消歧，而是使用序列標註模型（後面章節會講到）、語料中詞與詞的共現信息、詞的左熵（該詞左邊出現過的所有詞的信息熵之和）和右熵（該詞右邊出現過的所有詞的信息熵之和），以及一些詞典等方法來消歧。新詞發現技術也和這個技術差不多。

1.4　問題與思考

1．熵、相對熵和交叉熵的物理意義是什麽？

2．貝葉斯法則的優缺點是什麽，有哪些應用？

本文摘自《文本上的算法——深入淺出自然語言處理》

《文本上的算法——深入淺出自然語言處理》

路彥雄 著

點擊封面購買紙書

自然語言處理是研究人機之間用自然語言通信的理論和方法，是人工智能領域的一個重要分支，有著非常廣泛的應用空間。

本書結合作者多年學習和從事自然語言處理相關工作的經驗，力圖用生動形象的方式深入淺出地介紹自然語言處理的理論、方法和技術。本文拋棄繁瑣的證明，提取出算法的核心，幫助讀者盡快地掌握自然語言處理所必備的知識和技能。

通過本書，你將學習和理解：

★ 概率論、信息論、貝葉斯法則等基礎知識；

★ 機器學習和深度學習的熱門話題；

★ 程序優化的方法；

★
PageRank和相似度計算的原理；

★ 搜索引擎的原理、架構和核心模塊；

★ 各種推薦算法的原理和工作機制；

★ 自然語言處理和對話系統等技術難題。

本書適合從事自然語言處理相關研究和工作的讀者參考，尤其適合想要了解和掌握機器學習或者自然語言處理技術的讀者閱讀。

小福利

關註【異步社區】服務號，轉發本文至朋友圈或 50 人以上微信群，截圖發送至異步社區服務號後臺，並在文章底下留言，分享你的試讀體驗，我們將選出3名讀者贈送《文本上的算法——深入淺出自然語言處理》1本，趕快積極參與吧！ 活動截止時間：2018 年3月21日

在“異步社區”後臺回復“關註”，即可免費獲得2000門在線視頻課程；推薦朋友關註根據提示獲取贈書鏈接，免費得異步圖書一本。趕緊來參加哦！

掃一掃上方二維碼，回復“關註”參與活動！

閱讀原文，購買《文本上的算法——深入淺出自然語言處理》

閱讀原文

學習算法你必須知道的一些基礎知識（文末福利）