最大子段和

令f[i]為從莫一點開始到a[i]為止最大的子段和，則有以下轉移方程:

\[f_i = \max(f_{i-1} + a[i], a[i])\]

因為只需遍歷一次數組就可求出，所以復雜度為\(O(n)\)

package org.sequix.homework3;

/**
 * 提供求最大子段和的工具類。
 *
 * @author sequix
 * @version 0.0.1
 * @since 2018/03/26
 */
public class MaxSubArray {

    /**
     * 返回數組的最大子段和。
     * f[i] 到a[i]為止最大的子段和。
     * f[i] = max(f[i-1]+a[i], a[i])
 

     * 
     * @param arr 被求數組
     * @return 最大子段和
     */
    public static int msa(int[] arr) {
        if (arr.length == 0) {
            throw new IllegalArgumentException("expected a non-empty array");
        }
        
        int cur = arr[0];
        int ans = cur;
        
        for (int i = 1
 
, len = arr.length; i < len; ++i) {
            cur += arr[i];
            if (arr[i] > cur) cur = arr[i];
            if (cur > ans) ans = cur;
        }
        return ans;
    }
}

測試

為了方便的測試，這裏另寫了一個工具類TestUtils。

在TestUtils.msa中，以另一種方式求最大子段和。其枚舉所有的子段，選出最大的。此解法時間復雜度為\(O(n^2)\)，但其正確性顯而易見，所以用於對拍測試。

package org.sequix.homework3;

import java.util.Random;

/**
 * 提供測試用工具函數。
 * @author squix
 * @since 2018/03/19
 */
class TestUtils {
    private static Random random = new Random(); 
    
    /**
     * 生成[min, max]範圍內的隨機數。
     * @param min 最小值，最小可為Integer.MIN_VALUE
     * @param max 最大值，最大可為Integer.MAX_VALUE
     * @return 生成的隨機數
     */
    static int randomInteger(int min, int max) {
        long num = (long) max - min + 1;
        long kth = (long) (random.nextDouble() * num);
        long ret = (long) min + kth;
        return (int) ret;
    }
    
    /**
     * 生成隨機數數組。
     * @param size 數組大小
     * @param minElement 元素最小值
     * @param maxElement 元素最大值
     * @return 生成的數組
     */
    static int[] generateRandomArray(int size, int minElement, int maxElement) {
        int[] arr = new int[size];
        for (int i = 0; i < size; ++i)
            arr[i] = TestUtils.randomInteger(minElement, maxElement);
        return arr;
    }
    
    /**
     * 返回數組的最大子段和。用於和MaxSubArry.msa()對拍。
     * @param arr 被求數組
     * @return 最大子段和
     */
    static int msa(int[] arr) {
        int length = arr.length;
        int[] sum = new int[arr.length];
        
        sum[0] = arr[0];
        for (int i = 1; i < length; ++i) {
            sum[i] = sum[i-1] + arr[i];
        }
        
        int ans = arr[0];
        for (int left = 0; left < length; ++left) {
            for (int right = left; right < length; ++right) {
                int tmp = sum[right];
                if (left > 0) tmp -= sum[left-1];
                if (ans < tmp) ans = tmp;
            }
        }
        return ans;
    }
}

具體的測試類如下：

package org.sequix.homework3;

import static org.junit.Assert.assertEquals;

import org.junit.Test;
import org.junit.jupiter.api.RepeatedTest;
import org.junit.platform.runner.JUnitPlatform;
import org.junit.runner.RunWith;

/**
 * MaxSubArray 的測試類。
 *
 * @author sequix
 * @version 0.0.1
 * @since 2018/03/26
 */
@RunWith(JUnitPlatform.class)
public class MaxSubArrayTest {
    @Test(expected=IllegalArgumentException.class)
    public void testEmptyArray() {
        int[] original = new int[0];
        MaxSubArray.msa(original);
    }
    
    @Test
    public void testGeneral() {
        int[] original = new int[] {-2, 11, -4, 13, -5, -2};
        int expected = TestUtils.msa(original);
        assertEquals(expected, MaxSubArray.msa(original));
    }
    
    @Test
    public void testOnlyNegatives() {
        int[] original = TestUtils.generateRandomArray(10000, -10000, -1);
        int expected = TestUtils.msa(original);
        assertEquals(expected, MaxSubArray.msa(original));
    }
    
    @Test
    public void testOnlyPositives() {
        int[] original = TestUtils.generateRandomArray(10000, 1, 10000);
        int expected = TestUtils.msa(original);
        assertEquals(expected, MaxSubArray.msa(original));
    }
    
    @RepeatedTest(10)
    public void testRandom() {
        int[] original = TestUtils.generateRandomArray(10000, -10000, 10000);
        int expected = TestUtils.msa(original);
        assertEquals(expected, MaxSubArray.msa(original));
    }
}

測試效果

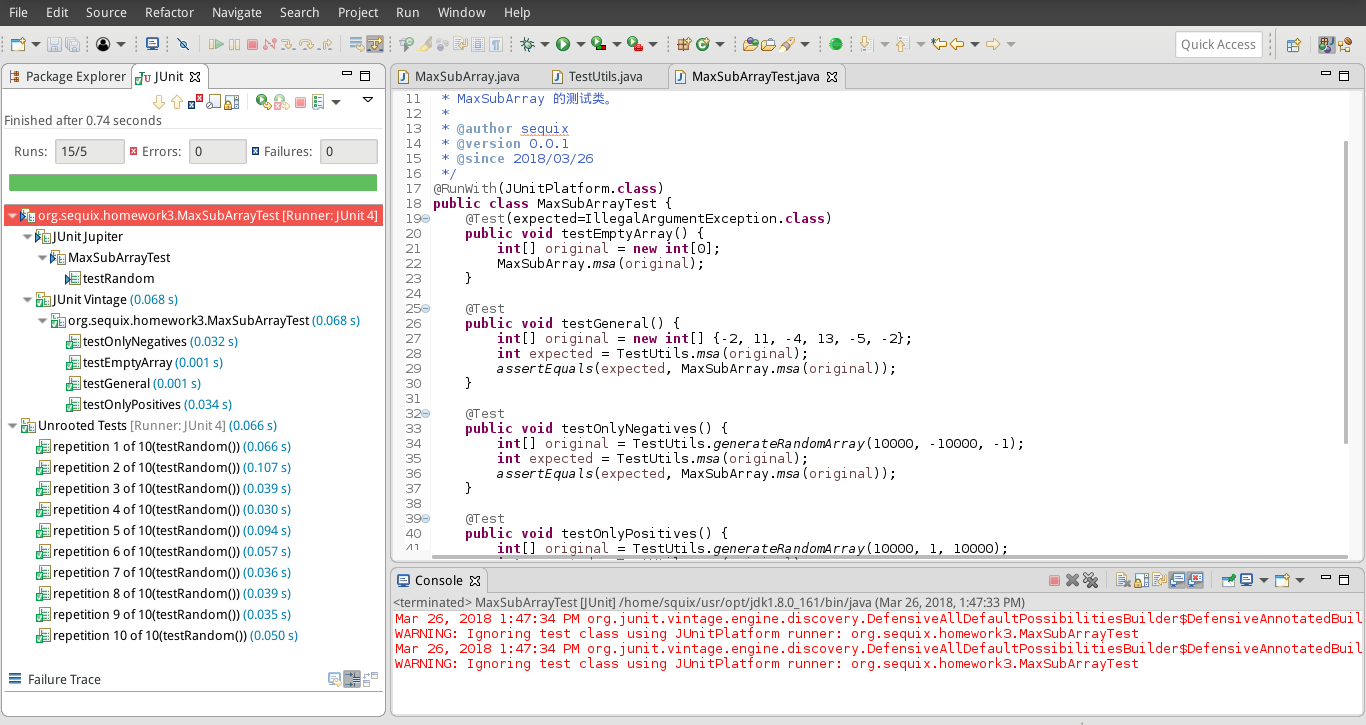
外鏈

代碼：Github

軟件工程（2018）第三次作業