spa fabs AD 大小 gid 圖1 ict 表示 分享圖片

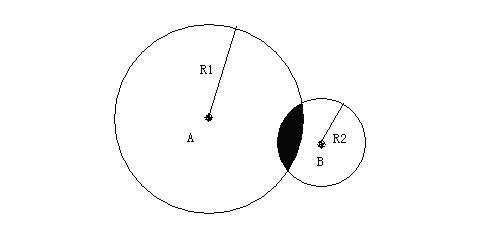
Problem Description There are two circles in the plane (shown in the below picture), there is a common area between the two circles. The problem is easy that you just tell me the common area.
Input There are many cases. In each case, there are two lines. Each line has three numbers: the coordinates (X and Y) of the centre of a circle, and the radius of the circle. Output For each case, you just print the common area which is rounded to three digits after the decimal point. For more details, just look at the sample. Sample Input 0 0 2
2 2 1 Sample Output

0.108
此題是求兩圓相交部分的面積。可分三大情況討論：

圖1 圖2

一、兩圓相離、外切或至少有一圓半徑為0：所求面積為0。
二、兩圓內切、內含：所求面積為小圓面積。
三、兩圓相交：這種情況分兩種小情況：１、兩圓心在公共弦的異側，如圖１所示；２、兩圓心在公共弦的同側如圖２所示。先看圖１，陰影部分可由公共弦AB分成兩個弓形，求出兩個弓形的面積相加即可，即S（陰影）　＝S（扇形O１AB）－S（三角形O１AB）＋S（扇形O２AB）－S（三角形O２AB）＝S（扇形O１AB）＋S（扇形O２AB）－S（四邊形O１AO２B），即兩扇形面積和與四邊面積之差。再來看圖２，這時所求面積為：S（扇形O１AB）－S（三角形O１AB）＋S（扇形O２AB<這裏的扇形為圓心角為2*y的扇形>）+S（三角形O２AB）=S（扇形O１AB）＋S（扇形O２AB）－S（四邊形O１AO２B），同樣為兩扇形面積和與四邊面積之差。因此這兩種小情況不必分開討論。（圖中a為圓心距，c為圓O1的半徑，z為圓O2的半徑，b為角AO1O2的大小，y為角AO2O1大小，A、B為公共弦的兩端點，O1、O2為兩圓的圓心）
以下為實現代碼：

#include<stdio.h>
#include<math.h>
int main()
{
    double q,w,m,n,a,b,c,x,y,z,PI;
    PI=2*asin(1.0);
    while(~scanf("%lf%lf%lf",&a,&b,&c)){
        scanf("%lf%lf%lf",&x,&y,&z);
        a=sqrt((a-x)*(a-x)+(b-y)*(b-y));//計算圓心距
        //如果兩圓相離、外切或至少一圓半徑為0時，那麽所求面積為0
 

        if(a>=c+z||!c||!z)x=0;
        //如果兩內切或內含，那麽所求面積為小圓面積
        else if(a<=fabs(z-c)){
            if(z>c)z=c;
            x=z*z*PI;
        }
        //如果兩圓相交，面積求解如下
        else{
            //由余弦定理求出公共弦在圓o1中對應的圓心角的一半
            b=acos((a*a+c*c-z*z)/(2*a*c));
            //由余弦定理求出公共弦在圓o2中對應的圓心角的一半
            y=acos((a*a+z*z-c*c)/(2*a*z));
            //計算圓o1中扇形面積
            m=b*c*c;
            //計算圓o2中扇形面積
            n=y*z*z;
            //計算圓o1中扇形所對應的三角形面積
            q=c*c*sin(b)*cos(b);
            //計算圓o2中扇形所對應的三角形面積
            w=z*z*sin(y)*cos(y);
            //q+w為圖中四邊形面積，兩扇形面積之和與四邊形面積之差即為
            //所求面積。在圖2中y為鈍角，計算出的面積w為負值，這時q+w
            //表示兩三角面積之差，剛好還是四邊形面積，因此對於圖1和圖
            //2不必分情況討論
            x=m+n-(q+w);
        }
        printf("%.3f\n",x);
    }
    return 0;
}

誠實的說：復制於該大佬的博客>> http://blog.sina.com.cn/s/blog_69c3f0410100rh9f.html

hdu 1798 Tell me the area 幾何