機器學習中的目標函數、損失函數、代價函數有什麽區別?
作者:zzanswer
鏈接:https://www.zhihu.com/question/52398145/answer/209358209
來源:知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請註明出處。
謝謝評論區
@阿薩姆 老師的建議,完善下答案:
首先給出結論:損失函數和代價函數是同一個東西,目標函數是一個與他們相關但更廣的概念,對於目標函數來說在有約束條件下的最小化就是損失函數(loss function)。
舉個例子解釋一下:(圖片來自Andrew Ng Machine Learning公開課視頻)
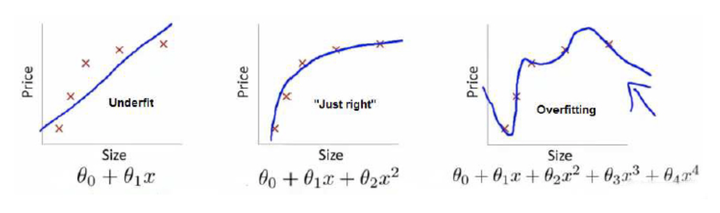
上面三個圖的函數依次為 ,
,
。我們是想用這三個函數分別來擬合Price,Price的真實值記為
我們給定 ,這三個函數都會輸出一個
,這個輸出的
與真實值
可能是相同的,也可能是不同的,為了表示我們擬合的好壞,我們就用一個函數來度量擬合的程度,比如:
,這個函數就稱為損失函數(loss function),或者叫代價函數(cost function)。損失函數越小,就代表模型擬合的越好。
那是不是我們的目標就只是讓loss function越小越好呢?還不是。
這個時候還有一個概念叫風險函數(risk function)。風險函數是損失函數的期望,這是由於我們輸入輸出的 遵循一個聯合分布,但是這個聯合分布是未知的,所以無法計算。但是我們是有歷史數據的,就是我們的訓練集,
到這裏完了嗎?還沒有。
如果到這一步就完了的話,那我們看上面的圖,那肯定是最右面的 的經驗風險函數最小了,因為它對歷史的數據擬合的最好嘛。但是我們從圖上來看
肯定不是最好的,因為它過度學習歷史數據,導致它在真正預測時效果會很不好,這種情況稱為過擬合(over-fitting)。
為什麽會造成這種結果?大白話說就是它的函數太復雜了,都有四次方了,這就引出了下面的概念,我們不僅要讓經驗風險最小化,還要讓結構風險最小化。這個時候就定義了一個函數 ,這個函數專門用來度量模型的復雜度
到這一步我們就可以說我們最終的優化函數是: ,即最優化經驗風險和結構風險,而這個函數就被稱為目標函數。
結合上面的例子來分析:最左面的 結構風險最小(模型結構最簡單),但是經驗風險最大(對歷史數據擬合的最差);最右面的
經驗風險最小(對歷史數據擬合的最好),但是結構風險最大(模型結構最復雜);而
達到了二者的良好平衡,最適合用來預測未知數據集。
以上的理解基於Coursera上Andrew Ng的公開課和李航的《統計學習方法》,如有理解錯誤,歡迎大家指正。
機器學習中的目標函數、損失函數、代價函數有什麽區別?
