原題鏈接

pdf

題目大意

給出一張無向圖圖，求該圖的最小瓶頸生成樹。

無向圖的瓶頸生成樹：無向圖\(G\)的一顆瓶頸生成樹是這樣的一顆生成樹：它最大的邊權值在\(G\)的所有生成樹中是最小的。瓶頸生成樹的值為\(T\)中最大權值邊的權。

該圖建立在坐標系中， 給出每個點的坐標。任意兩點之間都有邊，邊權即為兩點間的距離。

題解

由於只關心生成樹的最大值，我們可以將邊從小到大排序，依次加入（若構成環則不加入），直到構成一顆生成樹。

相信你已經發現了：這不就是Kruskal算法嗎？

於是，我們得出結論：無向圖的最小生成樹一定是瓶頸生成樹。

如果你仍然感到懷疑，那麽我們再用反證法證明：

假設存在一張無向圖的最小生成樹\(T\)

順便提一句，無向圖瓶頸生成樹一定是最小生成樹嗎？

看一看下圖就知道了：

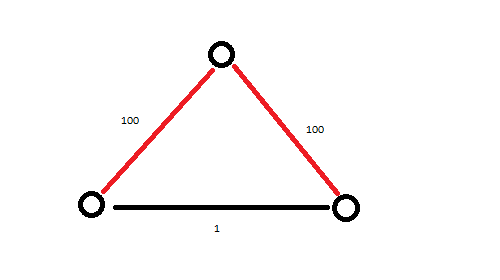
由於本題是稠密圖，最好用Prim解決（然而懶到家的我還是用了Kruskal）。

聽說有一種復雜度更優的算法叫Camerini‘s algorithm（然而我並不會），如果有大神會的話也可以教導我一下。

代碼

#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int maxn = 5005;

struct City
{
    double x, y;//註意是小數（開float似乎也行）
} city[maxn];

struct Edge
{
    int from, to;
    double dist;

    bool
 
 operator < (const Edge& other) const
    {
        return dist < other.dist;
    }
} edge[maxn*maxn];

int n, m, S;

inline double sqr(double a)
{
    return a*a;
}

inline double make_dist(City a, City b)
{
    return sqrt(sqr(a.x-b.x) + sqr(a.y-b.y));
}

inline void add_edge(City a, City b, int ai, int bi)
{
    double dist = make_dist(a, b);
    m++;
    edge[m].from = ai;
    edge[m].to = bi;
    edge[m].dist = dist;
}

inline void read()
{
    scanf("%d%d", &S, &n);
    S = n-S;
    for(int i = 1; i <= n; ++i)
    {
        scanf("%lf%lf", &city[i].x, &city[i].y);
        for(int j = 1; j < i; ++j)
            add_edge(city[i], city[j], i, j);
    }
}

struct UN_set
{
    int fa[maxn];

    inline void init(int n)
    {
        for(int i = 1; i <= n; ++i)
            fa[i] = i;
    }

    inline int getfa(int x)
    {
        return fa[x] == x ? x : fa[x] = getfa(fa[x]);
    }
} un;

inline double Kruskal()//其實最好還是用prim
{
    int tmp = 0;
    m = 0;
    read();
    sort(edge+1, edge+m+1);
    un.init(n);
    for(int i = 1; i <= m; ++i)
    {
        int ff = un.getfa(edge[i].from);
        int tf = un.getfa(edge[i].to);
        if(ff != tf)
        {
            un.fa[ff] = tf;
            tmp++;
            if(tmp == S)
                return edge[i].dist;
        }
    }
    return -1;
}

int main()
{
    int nnn;
    scanf("%d", &nnn);
    while(nnn--)
        printf("%.2f\n", Kruskal());//直接求最小生成樹即可
    return 0;
}

題解：UVa1025 A Spy in the Metro