limit app 很好 std 第一次 ive pro because 離線

Mishka and Interesting sum time limit per test 3.5 seconds memory limit per test 256 megabytes input standard input output standard output

Little Mishka enjoys programming. Since her birthday has just passed, her friends decided to present her with array of non-negative integers a

1, a2, ..., an of n elements!

Mishka loved the array and she instantly decided to determine its beauty value, but she is too little and can‘t process large arrays. Right because of that she invited you to visit her and asked you to process m queries.

Each query is processed in the following way:

1. Two integers l and r (1 ≤ l ≤ r ≤ n) are specified — bounds of query segment.
2. Integers, presented in array segment [l,  r] (in sequence of integers al, al + 1, ..., ar) even number of times, are written down.
3. XOR-sum of written down integers is calculated, and this value is the answer for a query. Formally, if integers written down in point 2 are x1, x2, ..., xk, then Mishka wants to know the value , where — operator of exclusive bitwise OR.

Since only the little bears know the definition of array beauty, all you are to do is to answer each of queries presented.

Input

The first line of the input contains single integer n (1 ≤ n ≤ 1 000 000) — the number of elements in the array.

The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — array elements.

The third line of the input contains single integer m (1 ≤ m ≤ 1 000 000) — the number of queries.

Each of the next m lines describes corresponding query by a pair of integers l and r (1 ≤ l ≤ r ≤ n) — the bounds of query segment.

Output

Print m non-negative integers — the answers for the queries in the order they appear in the input.

Examples input Copy

3
3 7 8
1
1 3

output Copy

0

input Copy

7
1 2 1 3 3 2 3
5
4 7
4 5
1 3
1 7
1 5

output Copy

0
3
1
3
2

Note

In the second sample:

There is no integers in the segment of the first query, presented even number of times in the segment — the answer is 0.

In the second query there is only integer 3 is presented even number of times — the answer is 3.

In the third query only integer 1 is written down — the answer is 1.

In the fourth query all array elements are considered. Only 1 and 2 are presented there even number of times. The answer is .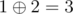

In the fifth query 1 and 3 are written down. The answer is .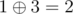

題意：m個詢問，每個詢問求一個區間內出現次數為偶的數的異或和

思路：一個區間所有數的異或和，等於這個區間內出現次數為奇的數的異或和，那麽這個區間內出現次數為偶的數的異或和就等於這個區間出現過的數的異或和異或上這個區間內所有數的異或和(也就是出現次數為奇的數在出現過的數中的補集)；

一個區間所有數的異或和很好求，只需記錄前綴異或和就可以了；那，一個區間內出現過的數的異或和怎麽求？總不能也維護一個前綴值把？因此，在線操作是沒辦法的；

采取離線操作，將每個詢問區間按右端點從小到大排序；依次處理排序後的區間；在這個區間[l,r]內，在某位置出現的數要在該位置標記為此數(更新)，若是該數在之前位置出現過了，將之前位置的該數消除(同樣是更新操作)——也就是對於重復出現的數，總是保留位置靠右的數；這樣，getsum(r)-getsum(l-1)將總是得到區間[l,r]內出現過的數的異或和；（太巧妙了%%%）

AC代碼:

#include <iostream>
#include<cstdio>
#include<map>
#include<algorithm>
#define lowbit(x) x&(-x)
using namespace std;

int n;
int a[1000010];
int sum[1000010];//前綴異或和
int c[1000010];//樹狀數組中的C數組
int ans[1000010];

struct Q{
  int l,r,ind;
}q[1000010];

bool cmp(Q a,Q b){
  return a.r<b.r;
}

map<int ,int> last;//記錄某個數出現的最後位置

void add(int x,int val){
  for(int i=x;i<=n;i+=lowbit(i)) c[i]^=val;
}

int getsum(int x){
  int ret=0;
  for(int i=x;i>0;i-=lowbit(i)) ret^=c[i];
  return ret;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) {scanf("%d",&a[i]); sum[i]=sum[i-1]^a[i];}
    int m;
    scanf("%d",&m);
    for(int i=1;i<=m;i++) {scanf("%d%d",&q[i].l,&q[i].r); q[i].ind=i;}
    sort(q+1,q+1+m,cmp);
    for(int pos=1,i=1;i<=m;i++){
        for(;pos<=q[i].r;pos++){
            add(pos,a[pos]);
            if(last[a[pos]]!=0) add(last[a[pos]],a[pos]);//如果a[pos]不是第一次出現，消除上次出現位置標記的a[pos]
            last[a[pos]]=pos;//將a[pos]出現的最後位置更新為pos
        }
        ans[q[i].ind]=sum[q[i].r]^sum[q[i].l-1]^getsum(q[i].r)^getsum(q[i].l-1);
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
    return 0;
}

[樹狀數組]Mishka and Interesting sum(codeforces703D)