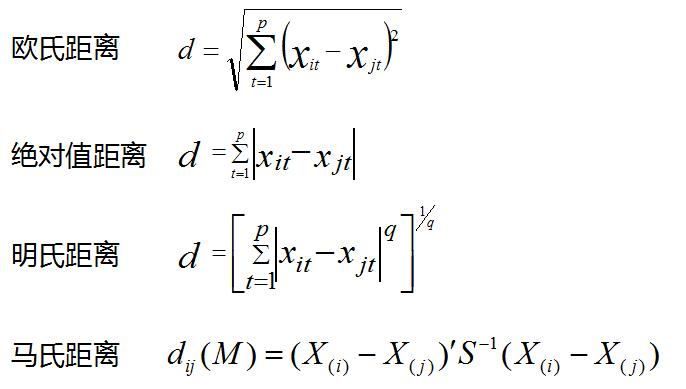高維數據的聚類分析

高維聚類研究方向

高維數據聚類的難點在於：

　　1、適用於普通集合的聚類算法，在高維數據集合中效率極低

　　2、由於高維空間的稀疏性以及最近鄰特性，高維的空間中基本不存在數據簇。

在高維聚類的研究中有如下幾個研究重點：

1）維度約簡，主要分為特征變換和特征選擇兩大類。前者是對特征空間的變換映射，常見的有PCA、SVD等。後者則是選擇特征的子集，常見的搜索方式有自頂向下、隨機搜索等；（降維）

2）高維聚類算法，主要分為高維全空間聚類和子空間聚類算法。前者的研究主要聚焦在對傳統聚類算法的優化改進上，後者則可以看做維度約簡的推廣；

子空間聚類：

　　選取與給定簇密切相關的維，然後在對應的子空間進行聚類。傳統的特征選擇算法可以用來確定相關維。

　　特征選擇算法綜述：http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html

　　不同的簇對應不同的子空間，並且每個子空間維數不同，因此也不可能一個子空間就可以發現所有的簇。為了解決這個問題，對全空間聚類進行了推廣，稱為子空間聚類（投影聚類）。

子空間聚類與基於降維的聚類對比

子空間聚類從某種程度上來講與基於降維的聚類有些類似，但後者是通過直接的降維來對高維數據進行預處理，即在降維之後的某一個特定的低維空間中進行聚類處理；而前者是把高維數據劃分成若幹不同的子空間，再根據需要在不同的子空間中尋求數據的聚類。

3）聚類有效性，是對量化評估方法的研究；

基於降維的聚類從根本上說都是以數據之間的距離 或相似度評價為聚類依據，當數據的維數不是很高時，這些方法效果較好，但當數據維度增高，聚類處理將很難達到預期的 效果。 原因在於：

ａ）在一個很高維的空間中定義一個距離度量本身就是一個很困難的事情；

ｂ）基於距離的方法通常需要計算各個聚類之間的距離均值，當數據的維度很高時，不同聚類之間的距離差異將會變得很小。

4）聚類結果表示方法；

5）高維數據索引結構；

6）高維離群點的研究

聚類︱python實現 六大 分群質量評估指標（蘭德系數、互信息、輪廓系數）

一、聚類分析的距離問題

聚類分析的目的就是讓類群內觀測的距離最近，同時不同群體之間的距離最大。

1.樣本聚類距離以及標準化

幾種常見的距離，歐氏距離、絕對值距離、明氏距離、馬氏距離。與前面不同的是，概率分布的距離衡量，K-L距離代表P、Q概率分布差的期望。

一般來說，聚類分析的數據都會進行標準化，標準化是因為聚類數據會受數據的量綱影響。

在以上的幾個距離明氏距離受量綱影響較大。馬氏距離受量綱影響較小

還有cos(余弦相似性)余弦值的範圍在[-1,1]之間，值越趨近於1，代表兩個向量的方向越趨近於0，他們的方向更加一致。相應的相似度也越高（cos距離可以用在文本挖掘，文本詞向量距離之上）。

幾種標準化的方法，有規範化、標準化（R語言︱數據規範化、歸一化）

2.不同類型變量距離計算

算法雜貨鋪——k均值聚類(K-means)

1、標量：歐幾裏得距離 曼哈頓距離 閔可夫斯基距離 標準化

標量也就是無方向意義的數字，也叫標度變量。現在先考慮元素的所有特征屬性都是標量的情況。例如，計算X={2,1,102}和Y={1,3,2}的相異度。一種很自然的想法是用兩者的歐幾裏得距離來作為相異度，歐幾裏得距離的定義如下：

其意義就是兩個元素在歐氏空間中的集合距離，因為其直觀易懂且可解釋性強，被廣泛用於標識兩個標量元素的相異度。將上面兩個示例數據代入公式，可得兩者的歐氏距離為：

除歐氏距離外，常用作度量標量相異度的還有曼哈頓距離和閔可夫斯基距離，兩者定義如下：

曼哈頓距離：

閔可夫斯基距離：

歐氏距離和曼哈頓距離可以看做是閔可夫斯基距離在p=2和p=1下的特例。另外這三種距離都可以加權，這個很容易理解，不再贅述。

下面要說一下標量的規格化問題。上面這樣計算相異度的方式有一點問題，就是取值範圍大的屬性對距離的影響高於取值範圍小的屬性。例如上述例子中第三個屬性的取值跨度遠大於前兩個，這樣不利於真實反映真實的相異度，為了解決這個問題，一般要對屬性值進行規格化。所謂規格化就是將各個屬性值按比例映射到相同的取值區間，這樣是為了平衡各個屬性對距離的影響。通常將各個屬性均映射到[0,1]區間，映射公式為：

其中max(ai)和min(ai)表示所有元素項中第i個屬性的最大值和最小值。例如，將示例中的元素規格化到[0,1]區間後，就變成了X’={1,0,1}，Y’={0,1,0}，重新計算歐氏距離約為1.732。

2、二元變量：相同序位同值屬性的比例 Jaccard系數

所謂二元變量是只能取0和1兩種值變量，有點類似布爾值，通常用來標識是或不是這種二值屬性。對於二元變量，上一節提到的距離不能很好標識其相異度，我們需要一種更適合的標識。一種常用的方法是用元素相同序位同值屬性的比例來標識其相異度。

設有X={1,0,0,0,1,0,1,1}，Y={0,0,0,1,1,1,1,1}，可以看到，兩個元素第2、3、5、7和8個屬性取值相同，而第1、4和6個取值不同，那麽相異度可以標識為3/8=0.375。一般的，對於二元變量，相異度可用“取值不同的同位屬性數/單個元素的屬性位數”標識。

上面所說的相異度應該叫做對稱二元相異度。現實中還有一種情況，就是我們只關心兩者都取1的情況，而認為兩者都取0的屬性並不意味著兩者更相似。例如在根據病情對病人聚類時，如果兩個人都患有肺癌，我們認為兩個人增強了相似度，但如果兩個人都沒患肺癌，並不覺得這加強了兩人的相似性，在這種情況下，改用“取值不同的同位屬性數/(單個元素的屬性位數-同取0的位數)”來標識相異度，這叫做非對稱二元相異度。如果用1減去非對稱二元相異度，則得到非對稱二元相似度，也叫Jaccard系數，是一個非常重要的概念。

3、分類變量

分類變量是二元變量的推廣，類似於程序中的枚舉變量，但各個值沒有數字或序數意義，如顏色、民族等等，對於分類變量，用“取值不同的同位屬性數/單個元素的全部屬性數”來標識其相異度。

4、序數變量：轉成標量

序數變量是具有序數意義的分類變量，通常可以按照一定順序意義排列，如冠軍、亞軍和季軍。對於序數變量，一般為每個值分配一個數，叫做這個值的秩，然後以秩代替原值當做標量屬性計算相異度。

5、向量：余弦相似度

對於向量，由於它不僅有大小而且有方向，所以閔可夫斯基距離不是度量其相異度的好辦法，一種流行的做法是用兩個向量的余弦度量，其度量公式為：

其中||X||表示X的歐幾裏得範數。要註意，余弦度量度量的不是兩者的相異度，而是相似度！

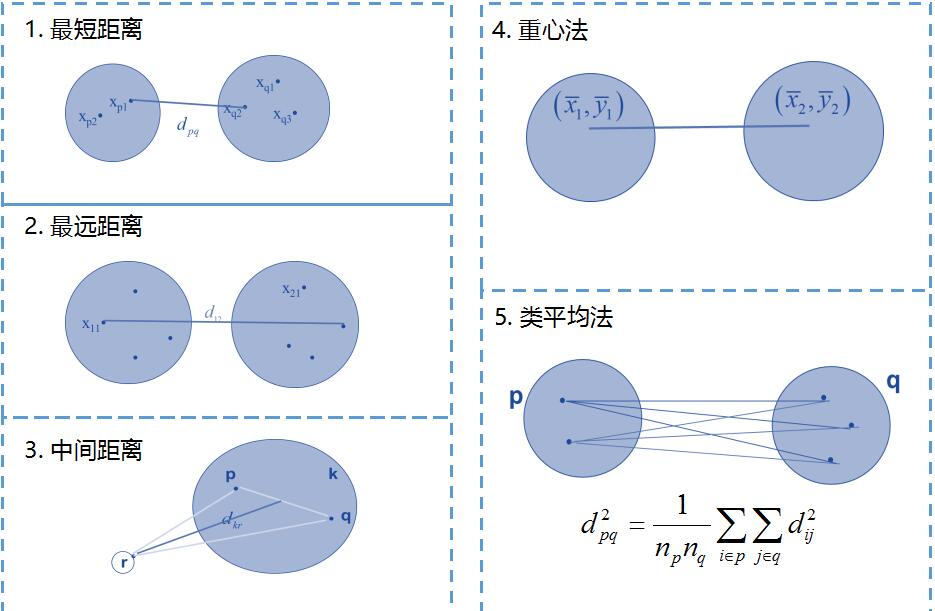
3.群體聚類距離

前面是樣本之間的距離，如果是一個點集，群落，如何定義群體距離。一般有以下幾種距離。

二.KMEANS註意點

1.K均值聚類算法對離群值最敏感，因為它使用集群數據點的平均值來查找集群的中心。

在數據包含異常值、數據點在數據空間上的密度擴展具有差異、數據點為非凹形狀的情況下，K均值聚類算法的運行結果不佳。

2.K均值對簇中心初始化非常敏感。

三.常見聚類模型的比較

四.聚類分群的數量如何確定？分群效果如何評價？

沒有固定標準，一般會3-10分群。或者用一些指標評價，然後交叉驗證不同群的分群指標。

一般的指標：輪廓系數silhouette（-1,1之間，值越大，聚類效果越好）（fpc包），蘭德指數rand；R語言中有一個包用30種方法來評價不同類的方法（NbClust），但是速度較慢。既可以確定分群數量，也可以評價聚類質量

商業上的指標：分群結果的覆蓋率；分群結果的穩定性；分群結果是否從商業上易於理解和執行

1 . 蘭德指數 需要標簽

蘭德指數（Rand index）需要給定實際類別信息$C$，假設$K$是聚類結果，$a$表示在$C$與$K$中都是同類別的元素對數，$b$表示在$C$與$K$中都是不同類別的元素對數，則蘭德指數為：

${\rm RI}=\frac{a+b}{C_2^{n_{\rm samples}}}$，

對於以上公式，

• 分子：屬性一致的樣本數，即同屬於這一類或都不屬於這一類。a是真實在同一類、預測也在同一類的樣本數；b是真實在不同類、預測也在不同類的樣本數；
• 分母：任意兩個樣本為一類有多少種組合，是數據集中可以組成的總元素對數；
• RI取值範圍為[0,1]，值越大意味著聚類結果與真實情況越吻合。

對於隨機結果，RI並不能保證分數接近零。為了實現“在聚類結果隨機產生的情況下，指標應該接近零”，調整蘭德系數（Adjusted rand index）被提出，它具有更高的區分度：

${\rm ARI}=\frac{{\rm RI}-E[{\rm RI}]}{\max({\rm RI})-E[{\rm RI}]}$，

具體計算方式參見Adjusted Rand index。

ARI取值範圍為$[-1,1]$，值越大意味著聚類結果與真實情況越吻合。從廣義的角度來講，ARI衡量的是兩個數據分布的吻合程度。

2. 互信息 需要標簽

互信息（Mutual Information）也是用來衡量兩個數據分布的吻合程度。假設$U$與$V$是對$N$個樣本標簽的分配情況，則兩種分布的熵（熵表示的是不確定程度）分別為：

$H(U)=\sum\limits_{i=1}^{|U|}P(i)\log (P(i)), H(V)=\sum\limits_{j=1}^{|V|}P‘(j)\log (P‘(j))$，

其中$P(i)=|U_i|/N,P‘(j)=|V_j|/N$。$U$與$V$之間的互信息（MI）定義為：

${\rm MI}(U,V)=\sum\limits_{i=1}^{|U|}\sum\limits_{j=1}^{|V|}P(i,j)\log\left ( \frac{P(i,j)}{P(i)P‘(j)}\right )$，

其中$P(i,j)=|U_i\bigcap V_j|/N$。標準化後的互信息（Normalized mutual information）為：

${\rm NMI}(U,V)=\frac{{\rm MI}(U,V)}{\sqrt{H(U)H(V)}}$。

與ARI類似，調整互信息（Adjusted mutual information）定義為：

${\rm AMI}=\frac{{\rm MI}-E[{\rm MI}]}{\max(H(U), H(V))-E[{\rm MI}]}$。

利用基於互信息的方法來衡量聚類效果需要實際類別信息，MI與NMI取值範圍為$[0,1]$，AMI取值範圍為$[-1,1]$，它們都是值越大意味著聚類結果與真實情況越吻合。

3. 輪廓系數

輪廓系數旨在將某個對象與自己的簇的相似程度和與其他簇的相似程度進行比較。輪廓系數最高的簇的數量表示簇的數量的最佳選擇。

輪廓系數（Silhouette coefficient）適用於實際類別信息未知的情況。對於單個樣本，設$a$是與它同類別中其他樣本的平均距離，$b$是與它距離最近不同類別中樣本的平均距離，輪廓系數為：

$s=\frac{b-a}{\max(a,b)}$。

對於一個樣本集合，它的輪廓系數是所有樣本輪廓系數的平均值。

輪廓系數取值範圍是$[-1,1]$，同類別樣本越距離相近且不同類別樣本距離越遠，分數越高。

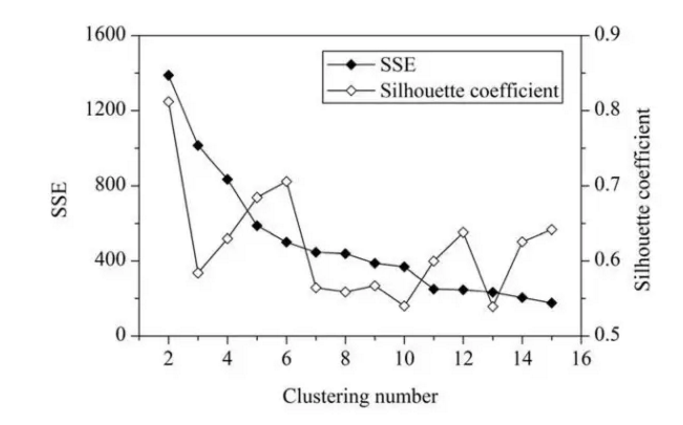
一般來說，平均輪廓系數越高，聚類的質量也相對較好。在這，對於研究區域的網格單元，最優聚類數應該是2，這時平均輪廓系數的值最高。但是，聚類結果（k=2）的 SSE 值太大了。當 k=6 時，SEE 的值會低很多，但此時平均輪廓系數的值非常高，僅僅比 k=2 時的值低一點。因此，k=6 是最佳的選擇。

聚類 高維聚類 聚類評估標準