博客園記--圖
1.1圖的思維導圖



1.2 圖結構學習體會:
深度遍歷算法和廣度遍歷算法:理解起來相對容易,尤其是在鄰接矩陣中,找起來很方便,重要的要做到不重不漏.兩種算法都是以鄰接表或鄰接矩陣為模板的算法,兩種算法能解決不同的問題。
Prim和Kruscal算法:都是從連通圖中找出最小生成樹的算法。Prim算法直接查找,多次尋找鄰邊的權重最小值,而Kruskal是需要先對權重排序後查找的,則Kruskal算法效率比Prim快。
Dijkstra算法:時間復雜度為O(n2),要很認真地去觀察新添頂點後,點與點之間的距離能不能更小,通過Dijkstra計算圖G中的最短路徑時,需要指定起點s,引進兩個集合S和U。S的作用是記錄已求出最短路徑的頂點(以及相應的最短路徑長度),而U則是記錄還未求出最短路徑的頂點。
拓撲排序算法:一定要有向圖,要去判斷有沒有環路,有環路則為錯誤.
2.PTA實驗作業(4分)
本周要求挑選出3道題目書寫設計思路、調試過程。設計思路使用偽代碼描述。題目選做要求:
7-1 圖著色問題(25 分)
代碼截圖:



設計思路(偽代碼或流程圖)
該問題需要我們遍歷找出有問題的子集,在我們進行遞歸查找的時候,其實可以立 flag, 在不滿足條件的情況給直接排出,跳出循環,從而減少問題的規模,,其實就是在遞歸遍歷的時候直接在遍歷到不符合情況的時候直接剔除完成篩選. 使用回溯法將visited數組初始化為0;依次觀察,若頂點之間的著色不沖突則轉下一步驟,否則繼續執行程序,若頂點全部著色,輸出visited.
pta 提交列表說明:

出現問題:
開始,出現編譯錯誤,在dev 可以運行,後來發現編譯錯誤是因為代碼使用的是C++,而PTA的初始編譯器是C,經發現並改正後得以解決。
7-2 排座位(25 分)
代碼截圖:


設計思路(偽代碼或流程圖)
用1表示是朋友,-1表示是對頭,這樣的話朋友兩頂點的權值為1,假設倆人A和B,假如A、B是直接的朋友,那麽我們直接輸出 No problem ,那假如A、B不敵對,就輸出OK ,假如A、B敵對但他們有共同的朋友,輸出OK but... (註意點的格式)權值為1.否則A、B敵對並且沒有共同的朋友,輸出No way,權值為-1.
pta 提交列表說明:
 出現問題:
出現問題:
一個原因還是因為我沒有在 pta 上改成需要的 c++, 還有一點是在 dev 運行的時候發現答案和輸出樣例不同,由於輸出時候的三個點打成中文的點.
7-5 暢通工程之最低成本建設問題(30 分)
代碼截圖:



設計思路(偽代碼或流程圖)
成本問題其實可以化作是最短路徑的問題,而我們可以用最小生成樹來求解該類的最短路徑問題,從給出的數據輸入建立帶權的無向圖,同時判斷兩頂點(兩城鎮)的
最短路徑,這樣既是最低成本的建設。
pta 提交說明:

出現問題:
該題應用到prim 算法,但是由於對Prim算法的熟練度不夠,導致在後期無法將子函數成功插入代碼,雖然書上有類似,但是需要進行部分改動,導致改動課本源代碼比較慢。同時程序很多地方的指針部分由於粗心忘記加*號,導致編譯錯誤.
本次題目集總分:165分
3.1PTA排名
28
3.2我的總分
165

代碼閱讀之拓撲算法
1、拓撲排序的介紹
對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序,是將G中所有頂點排成一個線性序列,使得圖中任意一對頂點u和v,若邊(u,v)∈E(G),則u在線性序列中出現在v之前。
拓撲排序對應施工的流程圖具有特別重要的作用,它可以決定哪些子工程必須要先執行,哪些子工程要在某些工程執行後才可以執行。為了形象地反映出整個工程中各個子工程(活動)之間的先後關系,可用一個有向圖來表示,圖中的頂點代表活動(子工程),圖中的有向邊代表活動的先後關系,即有向邊的起點的活動是終點活動的前序活動,只有當起點活動完成之後,其終點活動才能進行。通常,我們把這種頂點表示活動、邊表示活動間先後關系的有向圖稱做頂點活動網(Activity On Vertex network),簡稱AOV網。
一個AOV網應該是一個有向無環圖,即不應該帶有回路,因為若帶有回路,則回路上的所有活動都無法進行(對於數據流來說就是死循環)。在AOV網中,若不存在回路,則所有活動可排列成一個線性序列,使得每個活動的所有前驅活動都排在該活動的前面,我們把此序列叫做拓撲序列(Topological order),由AOV網構造拓撲序列的過程叫做拓撲排序(Topological sort)。AOV網的拓撲序列不是唯一的,滿足上述定義的任一線性序列都稱作它的拓撲序列。
2、拓撲排序的實現步驟
- 在有向圖中選一個沒有前驅的頂點並且輸出
- 從圖中刪除該頂點和所有以它為尾的弧(白話就是:刪除所有和它有關的邊)
- 重復上述兩步,直至所有頂點輸出,或者當前圖中不存在無前驅的頂點為止,後者代表我們的有向圖是有環的,因此,也可以通過拓撲排序來判斷一個圖是否有環。
3、拓撲排序示例手動實現
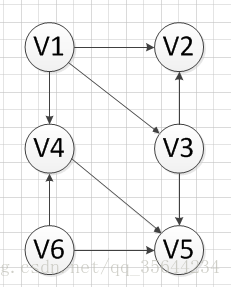
如果我們有如下的一個有向無環圖,我們需要對這個圖的頂點進行拓撲排序,過程如下:
首先,我們發現V6和v1是沒有前驅的,所以我們就隨機選去一個輸出,我們先輸出V6,刪除和V6有關的邊,得到如下圖結果:
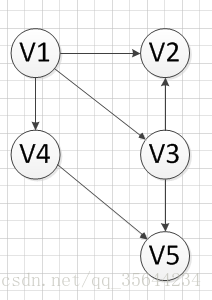
然後,我們繼續尋找沒有前驅的頂點,發現V1沒有前驅,所以輸出V1,刪除和V1有關的邊,得到下圖的結果:
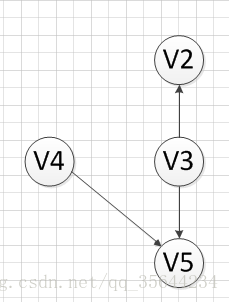
然後,我們又發現V4和V3都是沒有前驅的,那麽我們就隨機選取一個頂點輸出(具體看你實現的算法和圖存儲結構),我們輸出V4,得到如下圖結果:
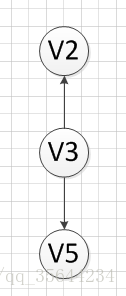
然後,我們輸出沒有前驅的頂點V3,得到如下結果:
然後,我們分別輸出V5和V2,最後全部頂點輸出完成,該圖的一個拓撲序列為:
v6–>v1—->v4—>v3—>v5—>v2
4、拓撲排序的代碼實現
下面,我們將用兩種方法來實現我麽的拓撲排序:
- Kahn算法
- 基於DFS的拓撲排序算法
首先我們先介紹第一個算法的思路:
Kahn的算法的思路其實就是我們之前那個手動展示的拓撲排序的實現,我們先使用一個棧保存入度為0 的頂點,然後輸出棧頂元素並且將和棧頂元素有關的邊刪除,減少和棧頂元素有關的頂點的入度數量並且把入度減少到0的頂點也入棧。具體的代碼如下:
bool Graph_DG::topological_sort() {
cout << "圖的拓撲序列為:" << endl;
//棧s用於保存棧為空的頂點下標
stack<int> s;
int i;
ArcNode * temp;
//計算每個頂點的入度,保存在indgree數組中
for (i = 0; i != this->vexnum; i++) {
temp = this->arc[i].firstarc;
while (temp) {
++this->indegree[temp->adjvex];
temp = temp->next;
}
}
//把入度為0的頂點入棧
for (i = 0; i != this->vexnum; i++) {
if (!indegree[i]) {
s.push(i);
}
}
//count用於計算輸出的頂點個數
int count=0;
while (!s.empty()) {//如果棧為空,則結束循環
i = s.top();
s.pop();//保存棧頂元素,並且棧頂元素出棧
cout << this->arc[i].data<<" ";//輸出拓撲序列
temp = this->arc[i].firstarc;
while (temp) {
if (!(--this->indegree[temp->adjvex])) {//如果入度減少到為0,則入棧
s.push(temp->adjvex);
}
temp = temp->next;
}
++count;
}
if (count == this->vexnum) {
cout << endl;
return true;
}
cout << "此圖有環,無拓撲序列" << endl;
return false;//說明這個圖有環
}
現在,我們來介紹第二個算法的思路:
其實DFS就是深度優先搜索,它每次都沿著一條路徑一直往下搜索,知道某個頂點沒有了出度時,就停止遞歸,往回走,所以我們就用DFS的這個思路,我們可以得到一個有向無環圖的拓撲序列,其實DFS很像Kahn算法的逆過程。具體的代碼實現如下:
bool Graph_DG::topological_sort_by_dfs() {
stack<string> result;
int i;
bool * visit = new bool[this->vexnum];
//初始化我們的visit數組
memset(visit, 0, this->vexnum);
cout << "基於DFS的拓撲排序為:" << endl;
//開始執行DFS算法
for (i = 0; i < this->vexnum; i++) {
if (!visit[i]) {
dfs(i, visit, result);
}
}
//輸出拓撲序列,因為我們每次都是找到了出度為0的頂點加入棧中,
//所以輸出時其實就要逆序輸出,這樣就是每次都是輸出入度為0的頂點
for (i = 0; i < this->vexnum; i++) {
cout << result.top() << " ";
result.pop();
}
cout << endl;
return true;
}
void Graph_DG::dfs(int n, bool * & visit, stack<string> & result) {
visit[n] = true;
ArcNode * temp = this->arc[n].firstarc;
while (temp) {
if (!visit[temp->adjvex]) {
dfs(temp->adjvex, visit,result);
}
temp = temp->next;
}
//由於加入頂點到集合中的時機是在dfs方法即將退出之時,
//而dfs方法本身是個遞歸方法,
//僅僅要當前頂點還存在邊指向其他不論什麽頂點,
//它就會遞歸調用dfs方法,而不會退出。
//因此,退出dfs方法,意味著當前頂點沒有指向其他頂點的邊了
//,即當前頂點是一條路徑上的最後一個頂點。
//換句話說其實就是此時該頂點出度為0了
result.push(this->arc[n].data);
}
兩種算法總結:
對於基於DFS的算法,增加結果集的條件是:頂點的出度為0。這個條件和Kahn算法中入度為0的頂點集合似乎有著異曲同工之妙,Kahn算法不須要檢測圖是否為DAG,假設圖為DAG,那麽在入度為0的棧為空之後,圖中還存在沒有被移除的邊,這就說明了圖中存在環路。而基於DFS的算法須要首先確定圖為DAG,當然也可以做出適當調整,讓環路的檢測測和拓撲排序同一時候進行,畢竟環路檢測也可以在DFS的基礎上進行。
二者的復雜度均為O(V+E)。
博客園記--圖