21.1.鏈式存儲的定義：

為了表示每個數據元素與其直接後繼之間的邏輯關系，數據元素除過存儲本身的信息之外，還需要存儲其後繼元素的地址信息。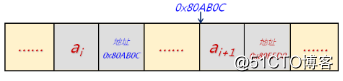

鏈式存儲結構的邏輯結構：

• 數據域：存儲數據元素本身
• 指針域：存儲相鄰節點的地址
  
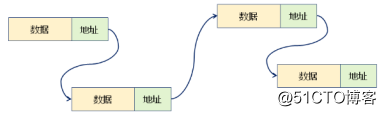
  統一的專業術語：
  — 順序表：—順序存儲結構的線性表
  — 鏈表：基於鏈式存儲的線性表
• 單鏈表：每個節點只包含直接後繼的地址信息
• 循環鏈表：單鏈表的最後一個節點的後繼為第一個節點
• 雙向鏈表：節點中包含其直接前驅和後繼的信息
  鏈表中基本概念：
  — 頭節點：鏈表中的輔助節點，包含指向第一個數據元素的指針，一般不包含數據。
  — 數據節點：鏈表中代表數據元素的節點，表現為：（數據元素、地址）
  
  — 尾節點：鏈表中最後一個節點，包含的地址信息為空

  21.2.單鏈表

  單鏈表中的節點定義：
  
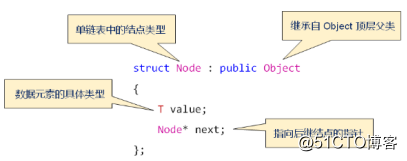
  註意：這裏的struct是用來定義一個類，與class的訪問屬性相反，默認為public
  單鏈表的內部結構：
  頭節點在單鏈表中的意義是：輔助數據元素的定位，方便插入和刪除，因此，頭節點不存儲實際的數據。
  

  21.3.單鏈表的插入與刪除：

  插入：

• 從頭節點開始，通過current指針定位到目標位置
• 從堆空間中申請新的Node節點
• 執行插入操作(註意先處理後半部分的掛接，否則會導致鏈表斷開，數據丟失，內存泄漏)

  node->value = e;
  node->next = current->next;
  Current->next = node;
   
  

  刪除：

• 從頭節點開始，通過current指針定位到目標位置
• 使用toDel指針指向需要刪除的節點

• 執行操作

  toDel = current->next;
  current->next = toDel->nex;
  delete toDel;

  22.單鏈表的實現

  22.1.設計要點和實現

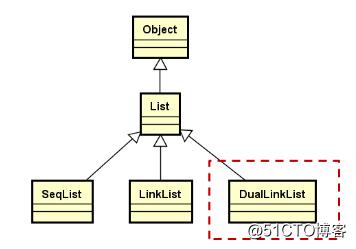
  類族結構：
  
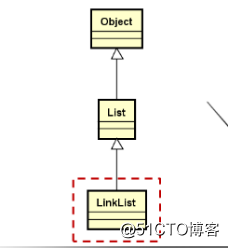
  — 類模板，通過頭節點訪問後繼節點
  — 定義內部節點的類型Node，用於描述數據域和指針域
  — 實現線性表的關鍵操作，增、刪、查等。

  template < typename T >
  class LinkList : public List<T>
  {
  protected:
  struct Node : public Object
  {
      Node * next;
      T value;
  };
  int m_length;
  mutable Node m_header;
  // 當前所找到的節點不是要直接操作的節點，要操作的是該節點的next
  Node *position(int i) const
  public:
  LinkList()
  bool insert(const T& e)
  bool insert(int index, const T& e)
  bool remove(int index)
  bool set(int index, const T& e)
  T get(int index)
  bool get(int index, T& e) const
  int length() const
  void clear()
  ~LinkList()
  };
   
  

  22.2.隱患和優化

  優化：
  代碼中多個函數存在對操作節點的定位邏輯。可以將該段代碼實現為一個position函數。

  Node *position(int i) const
  {
      Node *ret = reinterpret_cast<Node*>(&m_header);
  
      for(int p=0; p<i; p++)
      {
          ret = ret->next;
      }
  
      return ret;
  }

  隱患：
  
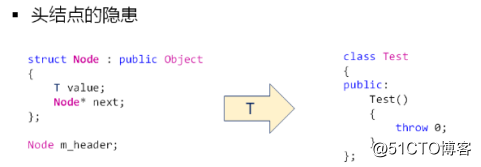
  LinkList<Test> L; // 拋出異常，分析為什麽我們沒有定義 Test 對象，但確拋出了異常
  原因在於單鏈表頭節點構造時會調用泛指類型的構造函數
  解決方案：
  頭節點構造時，避免調用泛指類型的構造函數，也即是說要自定義頭節點的類型，並且該類型是一個匿名類型

  mutable struct : public Object
  {
      char reserved[sizeof(T)];
      Node *next;
  }m_header;

  註意：這裏我們自定義都頭結點類型和Node的內存結構上要一模一樣（不要將兩個成員變量的位置交換）。

  22.3 單鏈表的最終實現

template <typename T>
class LinkList : public List<T>
{
protected:
    int m_length;
    int m_step;

    struct Node : public Object
    {
        Node* next;
        T value;
    };
    // 遊標,獲取遊標指向的數據元素,遍歷開始前將遊標指向位置為0的數據元素,通過節點中的next指針移動遊標
    Node* m_current;

    // 構造頭節點時，會調用泛指類型的構造函數，如果泛指類型構造函數中拋出異常，將導致構造失敗
    //mutable Node m_header;
    // 為了避免調用泛指類型的構造函數，自定義頭節點的類型(內存結構上要一模一樣)，並且該類型是一個匿名類型（沒有類型名）
    mutable struct : public Object
    {
        Node *next;
        char reserved[sizeof(T)];
    }m_header;

    Node* position(int index) const
    {
        Node* ret = reinterpret_cast<Node*>(&m_header);

        for(int p=0; p<index; p++)
        {
            ret = ret->next;
        }

        return ret;
    }

    virtual Node* create()
    {
        return new Node();
    }

    virtual void destroy(Node* pNode)
    {
        delete pNode;
    }

public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
        m_step = 0;
        m_current = NULL;
    }

    int find(const T& e) const
    {
        int ret = -1;
        Node* node = m_header.next;

        for(int i=0; i<m_length; i++)
        {
            if(node->value == e)
            {
                ret = i;
                break;
            }

            node = node->next;
        }

        return ret;
    }

    bool insert(const T& e)
    {
        return insert(m_length, e);
    }

    bool insert(int index, const T& e)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* node = create();
            if(NULL != node)
            {
                Node* current = position(index);

                node->next = current->next;
                current->next = node;
                node->value =e;
                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "no enough memory to insert node.");
            }
        }

        return ret;
    }

    bool remove(int index)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);

            Node* toDel = current->next;
            if( toDel ==  m_current)
            {
                m_current = toDel->next;    // 確保當前元素刪除後m_current指向正確的位置
            }
            current->next = toDel->next;
            destroy(toDel);
            m_length--;
        }

        return ret;
    }

    bool set(int index, const T& e)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);
            current->next->value = e;
        }

        return ret;
    }

    virtual T get(int index) const
    {
        T ret;

        if(get(index, ret))
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "index out of range.");
        }
    }

    bool get(int index, T& e) const
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);
            e = current->next->value;
        }

        return ret;
    }

    void traverse(void)     //O(n^2)
    {
        for(int i=0; i<length(); i++)
        {
            cout << (*this).get(i) << endl;
        }
    }

    void traverse_r(int i, int step = 1)     //O(n)
    {
        for((*this).move(i, step);!(*this).end();(*this).next())    //(*this).move(0,2)
        {
            cout << (*this).current() << endl;
        }
    }

    virtual bool move(int i, int step = 1)    // O(n)
    {
        bool ret = (0<=i)&&(i<m_length)&&(step>0);

        if(ret)
        {
            m_current = position(i)->next;
            m_step = step;
        }

        return ret;
    }

    virtual bool end()
    {
        return (m_current == NULL);
    }

    virtual T current()
    {
        if(!end())
        {
            return m_current->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException,"No value at current position...");
        }
    }

    virtual bool next()
    {
        int i =0;

        while((i<m_step)&&!end())
        {
            m_current = m_current->next;
            i++;
        }

        return(i == m_step);
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while(m_header.next)
        {
            Node* toDel = m_header.next;
            m_header.next = toDel->next;
            destroy(toDel);
            m_length--;
        }
    }

    ~LinkList()
    {
        clear();
    }

};

23.順序表和單鏈表的對比分析

23.1.代碼優化

1.查找操作：
可以為線性表list增加一個查找操作， int find (const T& e) const
參數為待查找的元素，返回值為查找到的元素首次出現的位置，沒有找到返回 -1
2.比較操作：
當我們定義的了上述查找函數之後，線性表中的數據為類類型時，查找函數編譯出錯，原因在於我們沒有重載==操作符。
解決的辦法，在頂層父類Object中重載==和!=操作符，並且讓自定義的類繼承自頂層父類Object。

23.2.對比分析

單鏈表和順序表的時間復雜度對比：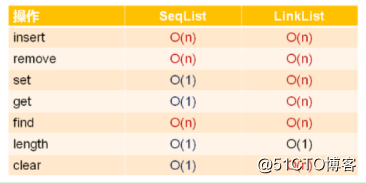

問題：
順序表的整體時間復雜度比單鏈表低，那麽單鏈表還有使用的價值嗎？實際工程中為什麽單鏈表反而用的比較多？
——實際工程中，時間復雜度只是效率的一個參考指標

• 對於內置基礎類型，順序表和單鏈表的效率不相上下（或者說順序表更優）
• 對於自定義類型，順序表在效率上低於單鏈表
  效率的深度分析：
  插入和刪除
  ——順序表：涉及大量數據對象的復制操作
  ——單鏈表只涉及指針操作，效率與對象無關
  數據訪問
  ——順序表：隨機訪問，可以直接定位數據對象
  ——單鏈表：順序訪問，必須從頭開始訪問數據無法直接定位
  工程開發中的選擇:
  順序表
  ——數據元素的類型相對簡單，不涉及深拷貝
  ——數據元素相對穩定，訪問操作遠遠多於插入和刪除
  單鏈表：
  ——數據元素相對復雜，復制操作相對耗時
  ——數據元素不穩定，需要經常插入和刪除，訪問操作較少
  總結：
• 線性表中元素的查找依賴於相等比較操作符（==）
• 順序表適用於訪問需求較大的場合（隨機訪問）
• 單鏈表適用於數據元素頻繁插入刪除的場合（順序訪問）
• 當數據元素類型相對簡單時，兩者效率不相上下

  24.單鏈表的遍歷與優化

  24.1.遍歷

  遍歷一個單鏈表的方法：通過for循環來調用get函數即可實現。

  for(int i=0; i<list.length(); i++)
  {
  cout << list.get(i) << endl;
  }

  這段代碼的時間復雜度為O（n^2）,所以我們希望對其優化，得到一個線性階的遍歷函數。

  24.2.設計思路：

• 在單鏈表的內部定義一個遊標（Node *m_current）
• 遍歷開始前將遊標指向位置為0的數據元素
• 獲取遊標指向的數據元素
• 通過節點中的next指針移動遊標
• 提供一組遍歷相關的函數，以線性的時間復雜度遍歷鏈表
  
  函數原型：

  bool move(int i, int step = 1);
  bool end();
  T current();
  bool next();

  24.3.優化

  單鏈表內部的一次封裝：

  virtual Node *create()
  {
      return new Node();
  }
  virtual void destory(Node *pn)
  {
      delete pn;
  }

  進行上述封裝得到意義：增加程序的可擴展性

  25.靜態單鏈表的實現

  25.1.單鏈表的缺陷：

  長時間使用單鏈表對象頻繁的增加和刪除數據元素，會導致堆空間產生大量的內存碎片，導致系統運行緩慢。
  新的線性表：
  在單鏈表的內部增加一片預留的空間，所有的node對象都在這篇空間中動態創建和動態銷毀。
  
  層次結構：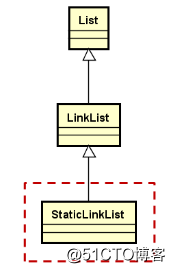
  

  25.2.設計思路：

• 類模板，繼承自LinkList
• 在類中定義固定大小的空間（unsigned char[N]）
• 重寫create和destroy函，改變內存的分配和歸還方式
• 在Node類中重載operator new，用於指定在內存上創建對象

template < typename T, int N>
class StaticLinkList : public LinkList<T>
{
protected:
    // (1)註意這裏不能直接寫為Node，編譯報錯，原因是Node中涉及泛指類型T，所以要聲明 LinkList<T>::Node
    // (2)上面的寫法在某些編譯情況下依然會報錯，原因在於，編譯器不知道這裏的Node是一個類對象，還是一個靜態成員對象，
    //    所以前面還需使用template聲明Node是一個類對象。
    typedef typename LinkList<T>::Node Node;
    struct SNode : public Node
    {
      void *operator new (unsigned int size, void *p)
      {
          (void)size;
          return p;
      }
    };

    unsigned char m_space[sizeof(SNode) *N];
unsigned int m_used[N];

   Node *create()
   {
        SNode *ret = NULL;

        for(int i=0; i<N; i++)
        {
            if( !m_used[i] )     // 0為空，1為有數據元素，不可用
            {
                ret = reinterpret_cast<SNode*>(m_space) + i;
                ret = new(ret)SNode;    //返回指定內存地址
                m_used[i] = 1;
                break;
            }
        }
        return ret;
   }

   void destroy(Node *pn)
   {
        SNode *space = reinterpret_cast<SNode *>(m_space);
        SNode *spn = dynamic_cast<SNode*>(pn);

        for(int i=0; i<N; i++)
        {
            if( pn == (space + i) )
            {
                m_used[i] = 0;
                spn->~SNode();      //直接調用析構函數
            }
        }
   }

public:
    StaticLinkList()
    {
        for(int i=0; i<N; i++)
        {
            m_used[i] = 0;
        }
    }

};

上節封裝create和destroy的意義：
為了本節實現StaticList 做準備，兩者的不同之處在於鏈表節點內存分配的不同，因此將僅有的不同封裝與父類和子類的虛函數中。最終通過多態技術，來實現。

25.3 靜態單鏈表的最終實現

template <typename T, int N>
class StaticLinkList : public LinkList<T>
{
protected:
    // typename 表明Node是一個類而非靜態成員變量，Node中包含泛指類型，所以使用 LinkList<T>指明
    typedef typename LinkList<T>::Node Node;
    struct SNode : public Node
    {
        // 重載後的結果，返回指定內存空間
        void* operator new(unsigned int size, void* p)
        {
            (void)size;
            return p;
        }
    };

    unsigned int m_space[N];
    unsigned int m_used[N];

    Node* create(void)
    {
        SNode* ret = NULL;

        for(int i=0; i<N; i++)
        {
            if(!m_used[i])
            {
                ret = reinterpret_cast<SNode*>(m_space) + i;
                ret = new(ret) SNode();     //返回指定內存空間
                break;
            }
        }
        return ret;
    }

    void destroy(Node* pn)
    {
        SNode* space = reinterpret_cast<SNode*>(m_space);
        SNode* spn = dynamic_cast<SNode*>(pn);

        for(int i=0; i<N; i++)
        {
            if(pn == space+i)
            {
                m_used[i] = 0;
                spn->~SNode();
                break;
            }
        }
    }

public:
    StaticLinkList()
    {
        for(int i=0; i<N; i++)
        {
            m_used[i] = 0;
        }
    }

    int capacity(void)
    {
        return N;
    }

/**
析構函數定義的原則：對於一個獨立類，構造函數中沒有使用系統資源，則可以不用定義析構函數，使用系統默認系統的即可。
但對於StaticLinkList這個類，繼承制LinkList，當我們沒有定義該類的析構函數時：在對象析構時，會默認去調用編譯器自己提供的析構函數，然後再調用其父類的析構函數，再其父類的析構函數中會調用clear函數，最終會調用父類的destroy函數。
在父類的destroy 中會使用delete去釋放堆空間，而我我們StaticLinkList中的數據並不是在堆空間的，所以會導致程序的不穩定。
解決辦法：自定義析構函數，最終調用子類的destroy函數。
**/
    ~StaticLinkList()
    {
        this->clear();
    }

};

29.循環鏈表

29.1.概念和結構

1.什麽是循環鏈表？
概念上：任意元素有一個前驅和後繼，所有數據元素的關系構成一個環
實現上：循環鏈表是一種特殊的鏈表，尾節點的指針保存了首節點的地址。
邏輯構成：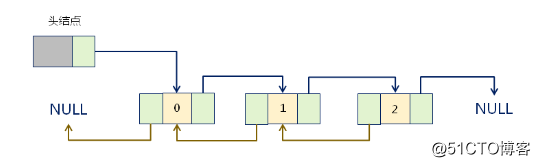

29.2.繼承關系和實現要點

實現思路：
1.通過模板定義CircleList類，繼承自LinkList類
2.定義內部函數last_to_first()用於將單鏈表首尾相連
3.特殊處理：
首元素的插入和刪除操作：
插入首元素時，先將頭結點和尾節點的指針指向要插入的元素，然後將要插入元素的指針指向之前的首節點；
刪除首節點時，首先將尾節點和頭的指針指向要刪除節點的下個節點）。
4.重新實現：清空操作和遍歷操作，註意異常安全（註意異常安全）。
循環鏈表可用於解決約瑟夫環的問題。
循環鏈表聲明：

template < typename T >
class CircleList : public LinkList<T>
{
protected:
    Node* last() const
    void last_to_first() const
    int mod(int i) const
public:
    bool insert(const T& e)
    bool insert(int index, const T& e)
    bool remove(int index)
    bool set(int index, const T& e)
    bool get(int index, const T& e) const
    T get(int index) const
    int find (const T& e) const
    void clear()
    bool move(int i, int step)
    bool end()
    ~CircleList()
};

註意：循環鏈表的實現中，查找和遍歷及清空操作要註意異常安全。不能改變鏈表的狀態（比如先將循環鏈表改為單鏈表，然後直接調用單鏈表的相關實現，最後再將鏈表首尾相連。這樣操作如果再過程中調用了泛指類型的構造函數，而且拋出異常，將導致循環鏈表變成單鏈表）。

29.3 循環鏈表的最終實現

template < typename T >
class CircleLinkList : public LinkList<T>
{
protected:
    typedef typename LinkList<T>::Node Node;
    int mod(int i)
    {
        return ( (this->m_length == 0) ? 0 : (i % this->m_length));
    }

    Node* last()
    {
        return this->position(this->m_length-1)->next;
    }

    void last_to_first()
    {
        last()->next = this->m_header.next;
    }

public:
    bool insert(const T& e)
    {
        return insert(this->m_length, e);
    }

    bool insert(int index, const T& e)
    {
        bool ret = true;
        index = index % (this->m_length + 1);   // 可插入點=length+1

        ret = LinkList<T>::insert(index, e);

        if(index == 0)
        {
            last_to_first();
        }

        return ret;
    }

    bool remove(int index)
    {
        bool ret = true;
        index = mod(index);

        if(index == 0)
        {
            Node* toDel = this->m_header.next;

            if(toDel != NULL)   // 類似於判斷index是否合法
            {
                this->m_header.next = toDel->next;
                this->m_length--;

                if(this->m_length > 0)
                {
                    last_to_first();
                    if(this->m_current == toDel)
                    {
                        this->m_current = toDel->next;
                    }
                }
                else
                {
                    this->m_current = NULL;
                    this->m_header.next = NULL;
                    this->m_length = 0;
                }
            }
            else
            {
                ret = false;
            }
        }
        else
        {
            ret = LinkList<T>::remove(index);
        }

        return ret;
    }

    T get(int index)
    {
        return LinkList<T>::get(mod(index));
    }

    bool get(int index, T& e)
    {
        return LinkList<T>::get(mod(index), e);
    }

    bool set(int index, const T& e)
    {
        return LinkList<T>::set(mod(index), e);
    }

    int find(const T& e) const
    {
        int ret = -1;
        Node* node = this->m_header.next;

        for(int i=0; i<this->m_length; i++)
        {
            if(node->value == e)
            {
                ret = i;
                break;
            }

            node = node->next;
        }

        return ret;
    }

    bool move(int i, int step)
    {
        return LinkList<T>::move(mod(i), step);
    }

    bool end()
    {
        return ( (this->m_current == NULL) || (this->m_length == 0) );
    }

    void clear()
    {
        if(this->m_length > 1)
        {
            remove(1);
        }
        if(this->m_length == 1)
        {
            Node* toDel = this->m_header.next;

            this->m_current = NULL;
            this->m_header.next = NULL;
            this->m_length = 0;

            this->destroy(toDel);
        }
    }

    ~CircleLinkList()
    {
        clear();
    }
};

數據結構(05)_單鏈表（單鏈表、靜態單鏈表、單向循環鏈表）