Capsule Network最大的特色在於vector in vector out & 動態路由算法。

vector in vector out

所謂vector in vector out指的是將原先使用標量表示的神經元變為使用向量表示的神經元。這也即是所謂的“Capsule”，“vector in vector out”或者“膠囊”所要表達的意思。按照Hinton的理解，每一個膠囊表示一個屬性，而膠囊的向量則表示該特征的某些“含義”。比如，之前我們使用標量表示有沒有羽毛，現在我們使用向量來表示，不僅表示有沒有，還表示了有什麽顏色，什麽材料的特征。也就是說將神經元從標量改為向量後，在特征提取時，對單個特征的表達更為豐富了。

這有些像NLP中的詞向量，之前使用的是one hot表示一個詞，只能表示有沒有該詞而已，引入了word2vec不但表示有沒有，而且能夠表示該詞的“意思”，表意更加豐富了。

部分人叫“Capsule Network膠囊網絡”為“張量網絡”

• 層層抽象，層層分類

  

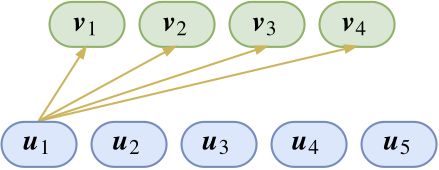
  上圖展示了特征\(u_1\)的連接，目前從上一層傳來的特征\(u_1\)假設表示羽毛，下一層抽取得到的\(v_1,v_2,v_3,v_4\)分別表示貓、狗、兔、鳥4個種類。可以很容易想到softmax:
  \[ (p_{1|1},p_{2|1},p_{3|1},p_{4|1})=\frac{1}{Z_1}(e^{u_1^T v_1},e^{u_1^T v_2},e^{u_1^T v_3},e^{u_1^T v_4}),\quad Z_1=\sum_{i=0}^4e^{u_1^T v_i} \]

  
  我們一般選擇最大的那個概率就行了，但是單靠這一個特征是不夠的，我們需要綜合各個特征，可以把上面的softmax對各個特征都做一遍，獲得\((p_{1|2},p_{2|2},p_{3|2},p_{4|2}),(p_{1|3},p_{2|3},p_{3|3},p_{4|3})...(p_{1|5},p_{2|5},p_{3|5},p_{4|5})\)。這時就需要融合這些特征，很容易想到“加權和”

  對於特征\(u_i\)，獲得的特征分布為\((p_{1|i},p_{2|i},p_{3|i},p_{4|i})\)，加權和就是：\(\sum_i u_ip_{j|i}(j=1,2,3,4)\)。對於希望獲得向上一層的特征\(v_j\)

  ，這裏paper中使用了一種squash函數處理後，就變成了向上一層的特征\(v_j\)，也即：
  \[ v_j=squash(\sum_i p_{j|i}u_i)=squash(\sum_i\frac{e^{u_i^T v_j}}{Z_i}u_i) \]
  所謂squash函數就是Capsule Network中的激活函數，和ReLU, tanh, sigmoid函數作用類似,原文中的函數如下:
  \[ squash(x)=\frac{||x||^2}{1+||x||^2}\frac{x}{||x||} \]
  後半部分\(\frac{x}{||x||}\)就是將向量模變為1，前半部分\(\frac{||x||^2}{1+||x||^2}\)是一個縮減函數，函數值始終小於1。在\(||x||\)近於0時有放大作用，\(||x||\)越大，越沒有影響。

  

  關於前半部分\(\frac{||x||^2}{1+||x||^2}\)，將模長壓縮至0~1有很多方法，比如\(tan||x||,1-e^{-||x||}\),是不是\(\frac{||x||^2}{1+||x||^2}\)這種壓縮方式最好；如果在中間層，這個壓縮處理是否有必要，由於有動態路由在裏面，即使去掉squash函數也具有非線性；另外分母上的常數1哪來的？可不可以嘗試其他常數實驗效果，這會是一個超參數嗎

  動態路由

  註意到：
  \[ v_j=squash(\sum_i p_{j|i}u_i)=squash(\sum_i\frac{e^{u_i^T v_j}}{Z_i}u_i) \]
  為了求\(v_j\)需要求softmax，而為了求softmax又需要知道\(v_j\)，似乎陷入了雞生蛋，蛋生雞的問題，這就是動態路由(Dynamic Routing)要解決的問題，它能夠“自主更新”參數，從而達到Hinton放棄梯度下降的目標。

  看一個NLP的例子，考慮一個向量\((x_1,x_2,...,x_n)\)，現在希望將n個向量整合成一個向量\(x\)(encoder)。簡化下情況，僅僅使用原來向量的線性組合，也就是:
  \[ x=\sum_{i=1}^n \lambda_ix_i \]
  這裏的\(\lambda_i\)相當於衡量了\(x\)與\(x_i\)的相似度，衡量了\(x_i\)在最終的\(x\)中的重要程度，這也是一個雞生蛋，蛋生雞的問題，解決方法就是叠代。定義一個基於softmax的相似度指標，然後“加權和”:
  \[ x=\sum_{i=1}^n\frac{e^{x^Tx_i}}{Z}x_i \]
  一開始，我們將\(x\)初始化為各個\(x_i\)的均值，然後將\(x\)帶入右側，左側得到一個新的\(x\)，然後再將其帶入右側，如此反復，一般叠代有限次即可收斂。

  為了得到得到各個\(v_j\)，一開始先將它們初始化為\(u_i\)的均值，然後帶入softmax叠代求解即可。事實上，輸出是輸入的聚類結果，而聚類通常都需要叠代算法，這個叠代算法即是“動態路由”。至於這個動態路由的細節，其實是不固定的，取決於聚類的算法。在Dynamic Routing Between Capsules. NIPS 2017 一文中，路由算法為：
  \[ \begin{aligned} &動態路由算法version1\\&初始化b_{ij}=0 \&叠代r次：\&\qquad c_i \gets softmax(b_i);\&\qquad s_j\gets\sum_ic_{ij}u_i;\&\qquad v_j\gets squash(s_j);\&\qquad b_{ij}\gets b_{ij}+u_i^Tv_j \end{aligned} \]
  這裏的\(c_{ij}\)即是前文中的\(p_{j|i}\)。

  這裏有人認為原文中的\(b_{ij}\gets b_{ij}+u_i^Tv_j\)有誤，應為\(b_{ij}\gets u_i^Tv_j\)。沒有看懂什麽意思，不作評價。

  補充下聚類算法K-Means的偽代碼：
  \[ \begin{aligned} 輸入：&樣本集D=\{x_1,x_2,...,x_m\};\&聚類簇數k.\過程：\&從D中隨機選擇k個樣本作為初始均值向量\{\mu_1,\mu_2,...,\mu_k\}\&repeat\&\quad 令C_i=\phi(1\leq i \leq k)\&\quad for\ j=1,2,...,m\ do\&\qquad 計算樣本x_j 與各個均值向量\mu_i(1\leq i\leq k)的距離：d_{ij}=||x_j-\mu_i||_2;\&\qquad 根據距離最近的均值向量確定x_j的簇標記:\lambda_j=argmax_{i\in\{1,2,...,k\}}d_{ij};\&\qquad 將樣本x_j劃入相應的簇:C_{\lambda_j}=C_{\lambda_j}\cup\{x_j\};\&\quad end\ for\&\quad for\ j=1,2,...,k\ do\&\qquad 計算新的均值向量：\mu_{i}‘=\frac{1}{|C_i|}\sum_{x\in C_i}x;\&\qquad 更新均值向量：\mu_i\gets\mu_{i}‘\& until\ 當前所有均值向量均不再更新 \end{aligned} \]
  類比下，這裏的\(x_1,x_2,...,x_m\)可以看作是上一層傳來的特征\(u_i\)；而獲得的聚類中心，即均值向量\(\mu_i\)可以看作是這層抽取得到的特征\(v_j\)。

  按照這個算法，\(v_j\)能夠叠代的算出來，那就真的拋棄反向傳播了，但事實上\(v_j\)是作為輸入\(u_i\)的某種聚類中心出現的，如果如此，各個\(v_j\)就都一樣了。上面類比的K-Means算法獲得聚類中心是需要一個參數“聚類簇數k”，這在動態路由中是沒有的，類似的，神經元需要從多個角度看輸入，從而得到不同的聚類中心。可以想象一個立方體，從正面獲得一個中心點，從側面又獲得一個，從上面的面又可以獲得一個中心點。為了實現“多角度看特征”，可以在上一層膠囊傳入下一層之前，乘上一個矩陣做變換，這種變換就是所謂的仿射變換，它給神經元看特征提供了“觀察角度”，這個矩陣現在還是需要反向傳播訓練得到的。那麽，
  \[ v_j=squash(\sum_i p_{j|i}u_i)=squash(\sum_i\frac{e^{u_i^T v_j}}{Z_i}u_i) \]
  就要變為：
  \[ v_j=squash(\sum_i\frac{e^{\hat{u_{j|i}}^Tv_j}}{Z_i}\hat{u_{j|i}}),\ 其中\hat{u_{j|i}}=W_{ji}u_i \]
  這裏的\(W_{ji}\)是待訓練的矩陣，這裏的乘法是矩陣乘法，矩陣乘向量，因此，Capsule Network變成了：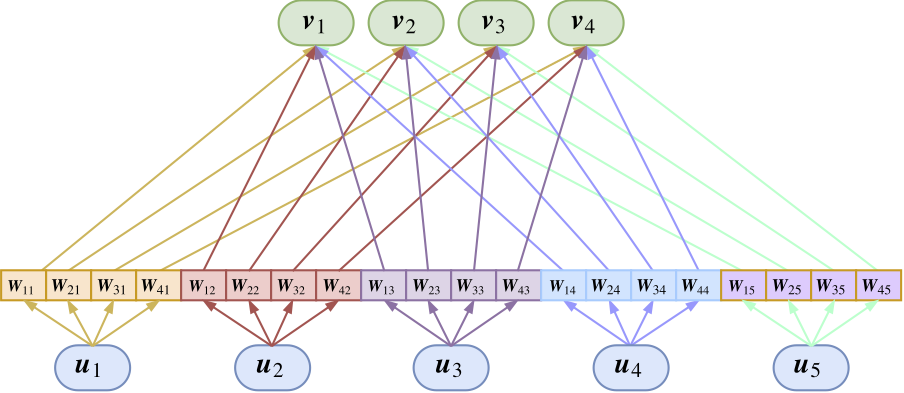

  

  完整的動態路由算法(Dynamic Routing Between Capsules. NIPS 2017中的動態路由)：
  \[ \begin{aligned} &動態路由算法version2\\&初始化b_{ij}=0 \&叠代r次：\&\qquad c_i \gets softmax(b_i);\&\qquad s_j\gets\sum_ic_{ij}\hat{u_{j|i}};\&\qquad v_j\gets squash(s_j);\&\qquad b_{ij}\gets b_{ij}+u_i^Tv_j \end{aligned} \]
  就是\(s_j\gets\sum_ic_{ij}u_i\)變為了\(s_j\gets\sum_ic_{ij}\hat{u_{j|i}}\)，新出來的\(\hat{u_{j|i}}\)由\(\hat{u_{j|i}}=W_{ji}u_i\)求得。

  這樣的Capsule層相當於普通神經網絡中的全連接層。

  進一步的，我們希望上一層的膠囊乘的“觀察角度矩陣”\(W\)能夠對上一層所有膠囊共享，就是變成這樣：

  

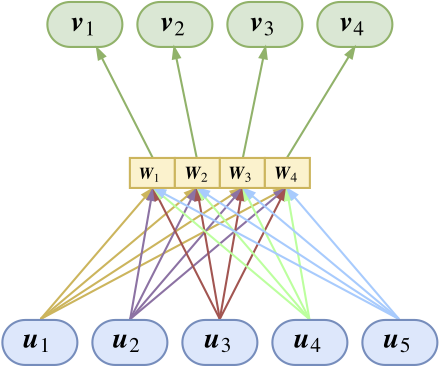
  這就是權值共享版的Capsule Network，所謂共享版，是指對於上一層傳來的膠囊\(u_i\)使用的變換矩陣是公用的，即\(W_{ji}\equiv W_j\)。這樣計算上面的\(\hat{u_{j|i}}\)就變成了\(\hat{u_{j|i}}=W_{j}u_i\)。

  可以看到，Capsule Network由於需要\(W\)做仿射變換，而\(W\)是通過反向傳播獲得的，因此Capsule Network還是存在反向傳播的。

總結

• Capsule Network將底層神經元由標量表示變為向量表示，這個向量表示就是“膠囊”。基於此，部分人認為“張量網絡”更為通俗易懂。

• Capsule Network與傳統神經網絡的對比：

  

  • Capsule Network的輸入輸出都是向量了，而非傳統網絡的標量。
  • 上一層傳入後，Capsule Network需要做一下放射變換(Affine Transformation)，提供不同的觀察角度，而傳統神經網絡並沒有這回事。
  • Capsule Network的非線性激活使用的是squash函數，而傳統的神經網絡是ReLU, tanh, sigmoid等。

• 原文中的動態路由偽代碼：

  

  對應的簡圖：

  

• 實驗上，Dynamic Routing Between Capsules. NIPS 2017 驗證了利用capsule作為神經元表示能個獲得特征更為豐富的語義，比如能夠捕獲到筆觸粗細，數字旋轉等信息。Capsule Network在該文4.1中顯示能夠去噪，而且表明Capsule Network能給出誤判的原因。Capsule Network還能有效地對重疊數字分割。

  實現

以廣泛傳播的CapsNet-Tensorflow，使用MNIST數據集，手寫數字識別為例。整個網絡分為兩個卷積層（包括普通的卷積層Conv1和Capsule版的卷積層PrimaryCaps）和一個全連接層（Capsule版的全連接層DigitCaps）

• Conv1 layer

  Input size	kernel size	conv stride	Channel	padding size	activation	pooling
  28x28x1	9x9	1x1	256	[0,0,0,0]	ReLU	No

  \[[None,28,28,1] -> [None,20,20,256]\]

  參數數量：9x9x256+256=20992

  備註：
  \[ 輸出神經元個數=(輸入神經元個數-卷積核大小+2*補零個數)/步長+1\20=(28-9+2*0)/1+1 \]

• PrimaryCaps layer

  

\[ [None,20,20,256]\rightarrow [None,6,6,32](8個卷積層並行)\rightarrow \left\{\begin{matrix} [None,6,6,1,32]\\ [None,6,6,1,32]\\ ...\\ [None,6,6,1,32] \end{matrix}\right.\rightarrow [None,6,6,8,32] \]

參數數量：9x9x256x32x8+8x32=5,308,672

相當於8個卷積層並行卷積，每次從各個卷積層拿出一個通道拼合出來，這就能得到了8維的向量，也就是標量變膠囊了。[None,6,6,8,32]的axis=0是batch_size；axis=1和axis=2是feature map的大小；axis=3是膠囊的維度，傳統的神經網絡這一維是沒有的，或者可以認為是1；axis=4是通道數。代碼實現：

• DigitCaps layer

  相當於全連接層，上一層6x6x32個capsule進，10個capsule出(表示0~9數字的概率)

  輸入：上一層PrimaryCaps輸出的6x6x32個capsule，每個capsule維度為[8,1]

  輸出：10個capsule，維度為[16,1]。輸出既然是向量而非傳統的一個個標量，這裏使用的是模長表示0~9數字的概率。為什麽使用模長，回憶上文中求\(s_j\)(沒有使用squash激活的\(v_j\))時，\(s_j\leftarrow \sum_i c_{ij}\hat{u_{j|i}}\)，這裏\(c_{ij}\)是softmax得到的概率，表示底層capsule在高層capsule中的重要程度，到了最後一層，就可以理解為哪個capsule是概率最大的輸出。所有的capsule都是經過了spuash將模規範化到0~1之間的，只有\(c_{ij}\)越大，向量模才能越大。這裏就是有人所說的神經元“競爭激活”的概念，\(c_{ij}\)越大，神經元就被激活。

  
  \[ [None,1152,8,1]\rightarrow[None,10,16,1] \]
  參數數量：

  1152x10個\(W_{ij}\): 1152x10x(8x16)=1,474,560

  1152x10個\(c_{ij}/b_{ij}\): 1152x10x1=11,520

改進的方向

• squash 函數，存在的必要存疑，以及對該函數本身的改進
• 動態路由，現在實際上是給了一個框，這個“路由”實際上是一個聚類，現在已經有了用EM做動態路由了，這是可以試試的坑
• 現有動態路由中有個\(b_{ij}\gets b_{ij}+u_i^Tv_j\)，有個哥們推導了一番，說這東西應該改為\(b_{ij}\gets u_i^Tv_j\)，這樣使得叠代輪數不是超參數，而是變成叠代輪數越大越好
• 神經元原先是一個標量，現在用向量表示，可不可以用矩陣，n維張量表示？

Connect

Email: [email protected]

GitHub: cnlinxi@github

後記

花了一周多理解Capsule Network，並且動手照著別人的Capsule Network代碼理解、默寫出來。今天寫完算是完成了一件事情。本文大多是拾人牙慧，但是也夾帶了自己的一些私貨，感謝這些博主和開源代碼貢獻者。

揭開迷霧，來一頓美味的Capsule盛宴

CapsNet-Tensorflow

Capsule Network