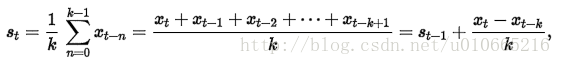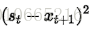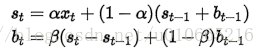Holt-Winters模型原理分析
Holt-Winters模型原理分析及代碼實現（python)
from：https://blog.csdn.net/u010665216/article/details/78051192引言
最近實驗室老師讓我去預測景區內代步車輛的投放量，於是乎，本著“一心一意地輸出年富力強的勞動力”這份初心，我就屁顛屁顛地去找資料，然後發現了Holt-Winters模型 , 感覺這個模型可以有，於是就去研究一番，並總結成這篇博客了。
原理分析
移動平均（The simple moving average (SMA)）
直觀上，最簡單的平滑時間序列的方法是實現一個無權重的移動平均，目前已知的方法是用窗口函數，平滑統計量 St就是最近k個觀察值的均值。公式如下：
這樣的方法存在明顯的缺陷，當k比較小時，預測的數據平滑效果不明顯，而且突出反映了數據最近的變化；當k較大時，雖然有較好的平滑效果，但是預測的數據存在延遲。而且最少需要k個值（窗口有限）。
加權移動平均
一種稍微復雜的方法是先選擇一組權重因子來計算加權移動平均 
然後用這些權重來計算這些平滑統計量：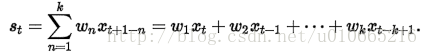 
在實踐中，通常在選擇權重因子時，賦予時間序列中的最新數據更大的權重，並減少對舊數據的權重。這個方法也需要最少k個值，並且計算復雜。
簡單指數平滑法
幸運地是有一種方法可以避免上述問題，它叫做指數平滑法。最簡單的指數平滑法如下：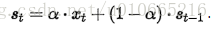 
其中α是平滑因子，0 < α < 1。換句話說，平滑統計值St是當前統計值Xt與上一時間平滑值St-1的加權平均。這個簡單指數平滑是很容易被應用的，因為只要有兩個觀察值就能計算了。這裏α的選取，我們可以采用最小二乘來決定α（最小化
為什麽被稱為“指數”平滑法
從它的遞推公式就能發現： 
簡單指數平滑法適用於沒有總體趨勢的時間序列。如果用來處理有總體趨勢的序列，平滑值將往往滯後於原始數據，除非α的值接近1，但這樣一來就會造成不夠平滑。
二次指數平滑
為了解決上述問題，於是引出了二次指數平滑，能夠保留總體趨勢信息。因為將指數平滑應用了兩次，所以被稱為二次指數平滑。與簡單指數平滑相比，二次指數平滑加入了時間趨勢統計量bt，公式如下：
若要預測Xt後m天，公式如下：
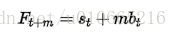
三次指數平滑
三次指數平滑將時間序列的季節性這一特征也考慮進去了。
季節性被定義為時間序列數據的趨勢，它表現出每一個周期重復自身的行為，就像任何周期函數一樣。“季節”這個詞用來表示行為每隔時間段L就開始自我重復。在自然界中有不同類型的季節性“累加性”(additive)和“累乘性“(multiplicative)，就像加法和乘法是數學的基本運算。
如果每個12月都比每個11月多賣出1000套公寓，我們就說這樣的季節趨勢是“累加性”的。可以用絕對增長來表示。如果我們在夏季比冬季多賣出10%的公寓，那麽季節趨勢在自然中是“累乘性”的。
累乘性公式如下：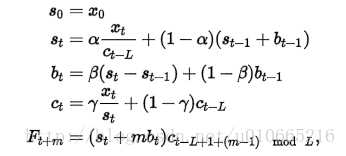 
其中 α是數據平滑因子， 0 < α < 1；β是趨勢平滑因子，0 < β < 1； γ是季節改變平滑因子0 < γ < 1。
初始化趨勢估計b0的公式為：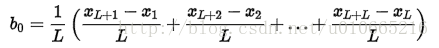 
累加性公式如下：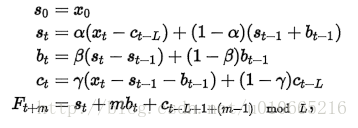 
對三次指數平滑法而言，我們必須初始化一個完整的“季節”Ci的值，不過我們可以簡單地設置為全1(針對累乘式)或全0(針對累加式)。只有當序列的長度較短時，我們才需要慎重考慮初始值的選取。
我們這裏講的Holt-Winters模型就是三次指數平滑法。哇，終於切入正題了。
所有的指數平滑法都要更新上一時間步長的計算結果，並使用當前時間步長的數據中包含的新信息。它們通過“混合”新信息和舊信息來實現，而相關的新舊信息的權重由一個可調整的拌和參數來控制。各種方法的不同之處在於它們跟蹤的量的個數和對應的拌和參數的個數。三次指數平滑法，功能最強大，既能體現趨勢性又能體現季節性，所以三次指數平滑法的參數最多，有三個。
Holt-Winters模型原理分析