啟發式合並

• 剛聽到這個東西的時候，我是相當蒙圈的。特別是“啟發式”這三個字莫名的裝逼，因此之前一直沒有學。
• 實際上，這個東西就是一個SB貪心。
• 以堆為例，若我們要合並兩個堆a、b，我們有一種極其簡單的做法：那就是比較一下它們的大小，將小的堆的每個元素依次插入到大的堆中。不妨設\(|a|≤|b|\)，則時間復雜度即為：\(O(|a|*log_2(|a|+|b|))\)。
• 這個東西看似很慢，但當點數較小的時候，我們可以證明復雜度是可被接受的。

• 比如我們要合並n個堆，這n個堆共有m個點。設這n個堆\(=\{s_1,s_2,s_3,...,s_n\}\)。
• 首先，我們合並\(s_1\)和\(s_2\)
  ，變成一個新的堆\(t_1\)。
• 然後，我們合並\(t_1\)和\(s_3\)，變成一個新的堆\(t_2\)。
• ……
• 以此類推，我們最終可以合並出一個堆\(t_{n-1}\)。

• 合並堆a、b時，記1次操作為將a中的一個元素插入b（或將b中的一個元素插入a）。
• 可以發現，第1次合並操作數\(≤|s_2|\)，第2次合並操作數\(≤|s_3|\)……第i次合並操作數\(≤|s_{i+1}|\)。
• 因此，總操作數\(≤\sum_{i=2}^n|s_i|≤m\)。而每次操作又是\(O(log_2m)\)的復雜度。因此：

• 時間復雜度：\(O(n+mlog_2m)\)。

  推廣

• 啟發式合並也可以用到set、splay、treap等平衡樹上去。
• 若我們要合並兩棵平衡樹a、b，也是先比較大小，將小的平衡樹的每個元素依次插入大的平衡樹。囿於插入的時間也是\(O(log_2n)\)，因此總復雜度還是\(O(|a|*log_2(|a|+|b|))\)。

• 註意：這裏的合並並非treap的merge。merge(a,b)是強行讓a所有元素的鍵值（要滿足二叉排序樹的性質的那個值）均小於b所有元素的鍵值，所以可以\(O(log_2n)\)做到；而這裏要合並的兩棵平衡樹a、b的鍵值可能是交錯不齊的。

  線段樹合並

• OI中常常遇到一些題目，要將若幹物件不斷合並，維護信息。
• 如果合並的順序不對，堆/平衡樹的啟發式合並會很慢。比如當你分治+啟發式合並的時候，時間復雜度就變成\(O(n*(log_2n)^2)\)
  了。

• 這個時候，就需要線段樹合並。

• 對於這個，相信大家都想得出下面這種合並步驟：
  
• 為了方便確定一棵樹是否為空，我們動態開點。
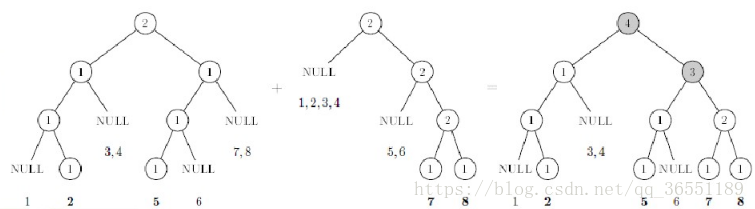
• 比如，我們合並兩棵權值線段樹：
  
• 顯然，這麽做的復雜度與兩棵樹公共的節點數成正比。
• 但是，假設我們要合並多棵線段樹呢？

• 假設我們要合並n棵線段樹，定義勢能函數\(\Phi(n)\)為它們的節點個數和。
• 每次合並線段樹a、b時，設其公共點數為c，則合並後的\(\Phi(n)\)減少c，而時間復雜度增加c。
• 因此，時間復雜度應≤節點個數和。
• 當線段樹中總共有m個元素時（比如n棵權值線段樹，只存有m個數），每個元素都可以動態開辟至多\(log_2n\)個節點。因此，此時的時間復雜度應為\(O(n+mlog_2n)\)。

• 註意：此時的時間復雜度並不受合並順序的限制。換句話說，不論你按什麽順序合並，只要你是合並n棵只有m個元素的線段樹，時間復雜度就是\(O(n+mlog_2n)\)。

  例題

  【BZOJ 2212】【Poi2011】 Tree Rotations
  【JZOJ5800】【洛谷P4416】 [COCI2017-2018#1] 被單

啟發式合並（堆、set、splay、treap）/線段樹合並學習小記