https://blog.csdn.net/libaqiangdeliba/article/details/41901387

1.基礎概念：

　　(1) 10折交叉驗證：英文名是10-fold cross-validation，用來測試算法的準確性。是常用的測試方法。將數據集分成10份。輪流將其中的9份作為訓練數據，1分作為測試數據，進行試驗。每次試驗都會得出相應的正確率(或差錯率)。10次的結果的正確率(或差錯率)的平均值作為對算法精度的估計，一般還需要進行多次10折交叉驗證，在求其平均值，對算法的準確性進行估計。

　　(2) 極大似然估計：極大似然估計，只是一種概率論在統計學中的應用，它是參數評估的方法之一。說的 已知某個隨機樣本滿足某種概率分布，但是其中具體的參數不清楚，參數估計通過若幹次實驗，觀察其結果，利用結果推出參數的大概值。極大似然估計是建立在這樣的思想上的：已知某個參數能使這個樣本出現的概率最大。我們當然不會再去選擇其他其他小概率的樣本，所以幹脆就把這個參數作為估計的真實值。

(3) 在信息論中，熵表示的是不確定性的量度。信息論的創始人香農在其著作《通信的數學理論》中提出了建立在概率統計模型上的信息度量。他把信息定義為”用來消除不確定性的東西“。熵的定義為信息的期望值。

　　ps:熵指的是體系的混亂程度，它在控制論，概率論，數論，天體物理，生命科學等領域都有重要的應用，在不同的學科中也有引申出更為具體的定義，是各個領域十分重要的參量。熵由魯道夫.克勞修斯提出，並應用在熱力學中。後來在，克勞德.埃爾伍德.香農 第一次將熵的概念引入到信息論中來。

　　(4) 後驗概率是信息論的基本概念之一。在一個通信系統中，在收到某個消息之後，接收端所了解到的該消息發送的概率稱為後驗證概率。後驗概率是指在得到”結果 “的信息後重新修正的概率，如貝葉斯公式中的。是執果尋因的問題。後驗概率和先驗概率有著不可分割的聯系，後驗的計算要以先驗概率為基礎，其實說白了後驗概率其實就是條件概率。

　　(5) PCA 主成分分析:

　　優點：降低數據的復雜性，識別最重要的多個特征。

　　缺點：不一定需要，且可能損失有用信息。

　　適用適用類型：數值型數據。

　　技術類型：降維技術。

　　簡述：在PCA中，數據從原來的坐標系轉換到了新的坐標系，新坐標系的選擇是由數據本身決定的。第一個新坐標軸選擇時原始數據中方差最大的方向，第二個新坐標軸的選擇和第一個坐標軸正交且具有最大方差的方向。該過程一直重復，重復次數為原始數據中特征的數目。會發現大部分方差都包含在最前面的幾個新坐標軸中。因此，可以忽略余下的坐標軸，即對數據進行了降維處理。除了PCA主成分分析技術，其他降維技術還有ICA(獨立成分分析)，因子分析等。

　　(6) 將不同的分類器組合起來，而這種組合結果則被稱為集成方法(ensemble method)或者元算法(meta-algorithm)。

　　(7) 回歸算法和分類算法很像，不過回歸算法和分類算法輸出標稱型類別值不同的是，回歸方法會預測出一個連續的值，即回歸會預測出具體的數據，而分類只能預測類別。

　　(8) SVD(singular value decomposition) 奇異值分解:

　　優點：簡化數據，去除噪聲，提高算法的結果。

　　缺點：數據轉換可能難以理解。

　　適用數據類型：數值型數據。

　　ps:SVD是矩陣分解的一種類型。

　　總結：SVD是一種強大的降維工具，我們可以利用SVD來逼近矩陣並從中提取重要特征。通過保留矩陣80%~90%的能量，就可以得到重要的特征並去掉噪聲。SVD已經運用到多個應用中，其中一個成功的應用案例就是推薦引擎。推薦引擎將物品推薦給用戶，協同過濾則是一種基於用戶喜好和行為數據的推薦和實現方法。協同過濾的核心是相似度計算方法，有很多相似度計算方法都可以用於計算物品或用戶之間的相似度。通過在低維空間下計算相似度，SVD提高了推薦引擎的效果。

　　(9)共線性：是指線性回歸模型中的解釋變量之間由於存在精確的相關關系或高度相關關系而使模型估計失真或難以估計。

　　2.基本算法

　　2.1 Logistic回歸：

　　優點：計算代價不高，易於理解和實現。

　　缺點：容易欠擬合，分類精度可能不高。

　　適用數據類型：數值型和標稱型數據。

　　類別：分類算法。

　　試用場景：解決二分類問題。

　　簡述：Logistic回歸算法基於Sigmoid函數，或者說Sigmoid就是邏輯回歸函數。Sigmoid函數定義如下：1/(1+exp(-z))。函數值域範圍(0,1)。可以用來做分類器。

　　Sigmoid函數的函數曲線如下：

　　邏輯回歸模型分解如下： (1)首先將不同維度的屬性值和對應的一組權重加和:

　　公式如下： z = w0+w1x1+w2x2+...+wm*xm。(其中x1,x2,...,xm是某樣本數據的各個特征，維度為m)

　　ps：這裏就是一個線性回歸。W權重值就是需要經過訓練學習到的數值，具體W向量的求解，就需要用到極大似然估計和將似然估計函數代入到 優化算法來求解。最常用的最後化算法有 梯度上升算法。

　　由上面可見：邏輯回歸函數雖然是一個非線性的函數，但其實其去除Sigmoid映射函數之後，其他步驟都和線性回歸一致。

　　(2)然後將上述的線性目標函數 z 代入到sigmond邏輯回歸函數，可以得到值域為(0,0.5)和(0.5,1)兩類值，等於0.5的怎麽處理還以自己定。這樣其實就得到了2類數據，也就體現了二分類的概念。

　　總結：Logistic回歸的目的是尋找一個非線性函數Sigmoid的最佳擬合參數，參數的求解過程可以由最優化算法來完成。在最優化算法中，最常用的就是梯度上升算法，而梯度上升算法有可以簡化為隨機梯度上升算法。

　　2.2 SVM(Support Vector Machines) 支持向量機：

　　優點：泛化錯誤率低，計算開銷不大，結果易解釋。

　　缺點：對參數調節和核函數的選擇敏感，原始分類器不加修改僅適用於處理二分類問題。

　　適用數據類型：數值型和標稱型數據。

　　類別：分類算法。

　　試用場景：解決二分類問題。

　　簡述：通俗的講，SVM是一種二類分類模型，其基本模型定義為特征空間上的間隔最大的線性分類器，即支持向量機的學習策略便是間隔最大化，最終可轉化為一個凸二次規劃問題的求解。或者簡單的可以理解為就是在高維空間中尋找一個合理的超平面將數據點分隔開來，其中涉及到非線性數據到高維的映射以達到數據線性可分的目的。

　　支持向量概念：

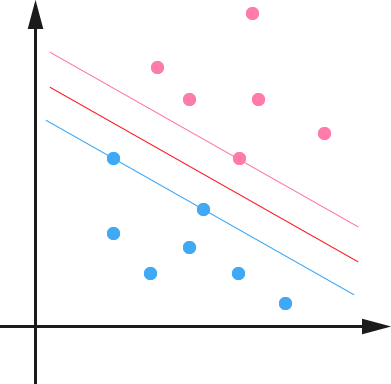
　　上面樣本圖是一個特殊的二維情況，真實情況當然可能是很多維。先從低緯度簡單理解一下什麽是支持向量。從圖中可以看到3條線，中間那條紅色的線到其他兩條先的距離相等。這條紅色的就是SVM在二維情況下要尋找的超平面，用於二分類數據。而支撐另外兩條線上的點就是所謂的支持向量。從圖中可以看到，中間的超平面和另外兩條線中間是沒有樣本的。找到這個超平面後，利用超平面的數據數學表示來對樣本數據進行二分類，就是SVM的機制了。

　　ps： 《機器學習實戰》書中有這麽幾個概念：

　　(1)如果能找到一個直線(或多維的面)將樣本點分開，那麽這組數據就是線性可分的。將上述數據集分隔開來的直線(或多維的面)稱為分隔超平面。分布在超平面一側的數據屬於一個類別，分布在超平面另一側的數據屬於另一個類別

　　(2)支持向量(Support vector)就是分離超平面最近的那些點。

　　(3)幾乎所有分類問題都可以使用SVM，值得一提的是，SVM本身是一個二分類分類器，對多類問題應用SVM需要對代碼做一些修改。

　　公式：

　　SVM有很多實現，但是本章值關註其中最流行的一種實現，及序列最小優化(Sequential Minimal Optimization，SMO)算法。

　　其公式如下：

　　SMO算法的目標是求出一些列的alpha，一旦求出了alpha，就很容易計算出權重向量w並得到分隔超平面。

　　SMO算法的工作原理是：每次循環中選擇兩個alpha進行優化處理。一旦找到一對合適的alpha，那麽就增大其中一個同時減小另一個。這裏所謂的“合適”就是指兩個alpha必須符合一定的條件，條件之一就是這兩個alpha必須要在間隔邊界之外，而其第二個條件則是這兩個alpha還沒有進行過區間化處理或者不在邊界上。

　　核函數將數據從低維度映射到高維：

　　SVM是通過尋找超平面將數據進行分類的，但是當數據不是線性可分的時候就需要利用核函數將數據從低維映射到高維使其線性可分後，在應用SVM理論。

　　示例：

　　這個二維數據分布不是線性可分的，其方程為：

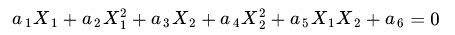
　　但是通過核函數維度映射後，其變為：

　　對應的方程為：

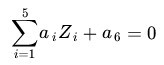
　　這樣映射後的數據就變成了線性可分的，就可以應用SVM理論了。

　　總結：支持向量機是一種分類器。之所以成為“機”是因為他會產生一個二值決策結果，即它是一種‘決策’機。核方法或者說核技巧會將數據(有時是非線性數據)從一個低維空間映射到一個高維空間，可以將一個在低維空間中的非線性問題轉換為高維空間下的線性問題來求解。

　　2.3 決策樹

　　： 優點：計算復雜度不高，輸出結果易於理解，對中間值的缺失不敏感，可以處理不相關特征數據。

　　缺點：可能會產生匹配過度問題。

　　適用數據類型：數值型和標稱型。

　　算法類型：分類算法。

　　數據要求：樹的構造只適用於標稱型的數據，因此數值型數據必須離散化。

　　簡述：在構造決策樹時，我們需要解決的第一個問題就是，當前數據集上哪個特征在劃分數據分類時起決定性作用。為了找到決定性特征，劃分出最好的結果，我們必須評估每個特征。完成測試後，原始數據就被劃分為幾個數據子集。這些數據的子集分布在第一個決策點的所有分支上，如果某個分支下的數據屬於同一個類型，則無需進一步對數據集進行切割。反之則需要進一步切割。

　　創建分支的偽代碼如下：

　　檢測數據集中的每個子項是否屬於同一分類：

　　if so return 類標簽;

　　else

　　尋找數據集的最好特征

　　劃分數據集

　　創建分支結點

　　for 每個劃分的子集

　　調用函數createBranch並增加返回結果到分支結點中

　　return 分支結點

　　在可以評測哪種數據劃分方式是最好的數據劃分之前，我們必須學習如何計算信息增益。集合的信息度量方式稱為香農熵或者簡稱為熵。熵在信息論中定義為信息的期望值。

　　信息熵的計算公式為：

　　H(信息熵) = -∑ P(xi) log2P(xi) ps:其中p(xi)表示選擇該分類的概率。

　　下面簡述一下生成決策樹的步驟：

　　(1) 根據給定的訓練數據，根據熵最大原則根據每一個維度來劃分數據集，找到最關鍵的維度。

　　(2) 當某個分支下所有的數據都數據同一分類則終止劃分並返回類標簽，否則在此分支上重復實施(1)過程。

　　(3) 依次計算就將類標簽構建成了一棵抉擇樹。

　　(4) 依靠訓練數據構造了決策樹之後，我們就可以將它用於實際數據的分類。

　　ps:當然生成決策樹的算法不止這一個，還有其他一些生成決策樹的方法，比如：C4.5和CART。

　　總結：

　　決策樹分類器就像帶有終止塊的流程圖，終止塊表示分類結果。開始處理數據集時，我們首先需要測量集合中數據的不一致性，也就是熵，然後尋找最優的方案劃分數據集，直到數據集中的所有數據屬於同一個分類。

　　2.4 樸素貝葉斯：

　　優點：在數據較少的情況下仍然有效，可以處理多類別問題。

　　缺點：對於輸入數據的準備方式較為敏感。

　　適用的數據類型：標稱型數據。

　　算法類型：分類算法

　　簡述：樸素貝葉斯是貝葉斯理論的一部分，貝葉斯決策理論的核心思想，即選擇具有高概率的決策。樸素貝葉斯之所以冠以樸素開頭，是因為其在貝葉斯理論的基礎上做出了兩點假設：

　　(1)每個特征之間相互獨立。

　　(2)每個特征同等重要。

　　貝葉斯準則是構建在條件概率的基礎之上的，ps：P(H|X)是根據X參數值判斷其屬於類別H的概率，稱為後驗概率。P(H)是直接判斷某個樣本屬於H的概率，稱為先驗概率。P(X|H)是在類別 H中觀測到X的概率(後驗概率)，P(X)是在數據庫中觀測到X的概率。可見貝葉斯準則是基於條件概率並且和觀測到樣本的先驗概率和後驗概率是分不開的。

　　總結：對於分類而言，使用概率有事要比使用硬規則更為有效。貝葉斯概率及貝葉斯準則提供了一種利用已知值來估計未知概率的有效方法。可以通過特征之間的條件獨立性假設，降低對數據量的需求。盡管條件獨立性的假設並不正確，但是樸素貝葉斯仍然是一種有效的分類器。

　　2.5 K-近鄰算法(KNN):

　　優點：精度高、對異常值不敏感、無數據輸入假定。

　　缺點：計算復雜度高，空間復雜度搞。

　　適用數據範圍：數值型和標稱型。

　　算法類型：分類算法。

　　簡述：算法原理，存在一個樣本數據集合，也稱作訓練樣本集，並且樣本集中每個數據都存在標簽，即我們知道樣本集中每一個數據與所屬分類的對應關系。輸入沒有標簽的新數據後，將新數據的每個特征和樣本集中數據對應的特征進行比較，然後算法提取樣本集中特征最相似數據(最近鄰)的分類標簽。一般來說，我們只選擇樣本數據集中前k個最相似的數據，這就是k-近鄰算法中k的出處，通常k是不大於20的整數。最後選擇k個最相似數據中出現次數最多的分類，作為新數據的分類。

　　2.6 線性回歸(Linear Regression)：

　　優點：結果易於理解，計算上不復雜。

　　缺點：對非線性數據擬合不好。

　　適用數據類型：數值型和標稱型數據。

　　算法類型：回歸算法。

　　ps:回歸於分類的不同，就在於其目標變量時連續數值型。

　　簡述：在統計學中，線性回歸(Linear Regression)是利用稱為線性回歸方程的最小平方函數對一個或多個自變量和因變量之間關系進行建模的一種回歸分析。這種函數是一個或多個稱為回歸系數的模型參數的線性組合(自變量都是一次方)。只有一個自變量的情況稱為簡單回歸，大於一個自變量情況的叫做多元回歸。

　　線性方程的模型函數的向量表示形式為：

　　通過訓練數據集尋找向量系數的最優解，即為求解模型參數。其中求解模型系數的優化器方法可以用“最小二乘法”、“梯度下降”算法，來求解損失函數：

　　附加：嶺回歸(ridge regression):

　　嶺回歸是一種專用於共線性數據分析的有偏估計回歸方法，實質上是一種改良的最小二乘估計法，通過放棄最小二乘法的無偏性，以損失部分信息、降低精度為代價，獲得回歸系數更為符合實際、更可靠的回歸方法，對病態數據的耐受性遠遠強於最小二乘法。

　　嶺回歸分析法是從根本上消除復共線性影響的統計方法。嶺回歸模型通過在相關矩陣中引入一個很小的嶺參數K(1>K>0)，並將它加到主對角線元素上，從而降低參數的最小二乘估計中復共線特征向量的影響，減小復共線變量系數最小二乘估計的方法，以保證參數估計更接近真實情況。嶺回歸分析將所有的變量引入模型中，比逐步回歸分析提供更多的信息。

　　總結：與分類一樣，回歸也是預測目標值的過程。回歸與分類的不同點在於，前者預測連續型的變量，而後者預測離散型的變量。回歸是統計學中最有力的工具之一。在回歸方程裏，求得特征對應的最佳回歸系統的方法是最小化誤差的平方和。

　　2.7 樹回歸:

　　優點：可以對復雜和非線性的數據建模。

　　缺點：結果不易理解。

　　適用數據類型：數值型和標稱型數據。

　　算法類型：回歸算法。

　　簡述：線性回歸方法可以有效的擬合所有樣本點(局部加權線性回歸除外)。當數據擁有眾多特征並且特征之間關系十分復雜時，構建全局模型的回歸算法是比較困難的。此外，實際中很多問題為非線性的，例如常見的分段函數，不可能用全局線性模型類進行擬合。樹回歸將數據集切分成多份易建模的數據，然後利用線性回歸進行建模和擬合。較為經典的樹回歸算法為CART(classification and regreesion trees 分類回歸樹)。

　　CART算法的詳細描述可以看這篇文章：http://box.cloud.taobao.com/file/downloadFile.htm?shareLink=1GIQrknG (說實話，大體了解，看的不太懂,誰了解的比較透徹可以分享下)。

　　2.8 K-Means(K 均值算法)：

　　優點：容易實現。

　　缺點：可能收斂到局部最小值，在大規模數據集上收斂較慢。

　　適用數據類型：數值型數據。

　　算法類型：聚類算法。

　　ps:K-Means和上面的分類和回歸算法不同，它屬於非監督學習算法。類似分類和回歸中的目標變量事先並不存在。與前面“對於數據變量X能預測變量 Y”不同的是，非監督學習算法要回答的問題是：“從數據X中能發現什麽?“，這裏需要回答的X方面可能的問題是：”構成X的最佳6個數據簇都是哪些“或者”X中哪三個特征最頻繁共現?“。

　　K-Means的基本步驟：

　　(1) 從數據對象中隨機的初始化K個初始點作為質心。然後將數據集中的每個點分配到一個簇中，具體來講每個點找到距其最近的質心，並將其分配給該質心所對應的簇。

　　(2) 計算每個簇中樣本點的均值，然後用均值更新掉該簇的質心。然後劃分簇結點。

　　(3) 叠代重復(2)過程，當簇對象不再發生變化時，或者誤差在評測函數預估的範圍時，停止叠代。

　　算法的時間復雜度上界為O(nkt), 其中t是叠代次數。

　　ps:初始的K個質心的選取以及距離計算公式的好壞，將影響到算法的整體性能。

　　附加：

　　二分K-均值算法:為克服K-均值算法收斂於局部最小值的問題，有人提出了另一個稱為二分K-均值(bisecting K-Means)的算法。該算法首先將所有點作為一個簇，然後將簇一分為二。之後選擇其中一個簇繼續劃分，選擇哪個一簇進行劃分取決於對其劃分是否可以最大程度降低SSE(Sum of Squared Error，兩個簇的總誤差平方和)的值。

　　2.9 算法關聯分析:

　　首先了兩個概念：

　　頻繁項集(frequent item sets):經常出現在一塊的物品的集合。

　　關聯規則(association rules)：暗示兩種物品間可能存在很強的關系。

　　項集的支持度(support)：數據集中包含該項集記錄所占的比例。

　　關聯分析的目標包括兩項：發現頻繁項集合發現關聯規則。首先找到頻繁項集，然後才能獲得關聯規則。

　　Apriori算法：

　　優點：易編碼實現。

　　缺點：在大型數據集上可能較慢。

　　適用數據類型：數值型或標稱型數據。

　　原理：如果某個項集時頻繁的，那麽他的所有子集也是頻繁的。

　　Apriori運用的DEMO示例參見博客：http://blog.csdn.net/lantian0802/article/details/38331463

　　簡述：

　　Apriori算法是發現頻繁項集的一種方法。Apriori算法的兩個輸入參數分別是最小支持度和數據集。該算法首先會生成所有單個item的項集列表。然後掃描列表計算每個item的項集支持度，將低於最小支持度的item排除掉，然後將每個item兩兩組合，然後重新計算整合後的item列表的支持度並且和最小支持度比較。重復這一過程，直至所有項集都被去掉。

　　總結：

　　關聯分析是用於發現大數據集中元素間有趣關系的一個工具集，可以采用兩種方式來量化這些有趣的關系。發現元素間不同的組合是個十分耗時的任務，不可避免需要大量昂貴的計算資源，這就需要一些更智能的方法在合理的時間範圍內找到頻繁項集。能夠實現這一目標的一個方法是Apriori算法，它使用 Apriori原理來減少在數據庫上進行檢查的集合的數目。Apriori原理是說如果一個元素是不頻繁的，那麽那些包含該元素的超集也是不頻繁的。 Apriori算法從單元素項集開始，通過組合滿足最小支持度要求的項集來形成更大的集合。支持度用來度量一個集合在原始數據中出現的頻率。

　　2.10 FP-growth算法：

　　簡述：FP-growth也是用於發現頻繁項集的算法，他以FP樹的結構存儲構建元素，其他Apriori算法的性能要好很多。通常性能要好2個數量級以上。其發現頻繁項集的過程如下：(1)構建FP樹。(2)從FP樹中挖掘頻繁項集。

　　優點：一般要快於Apriori。

　　缺點：實現比較困難，在某些數據集上性能會下降。

　　適用數據類型：標稱型數據。

　　總結：FP-growth算法是一種用於發現數據集中頻繁模式的有效方法。FP-growth算法利用Apriori原則，執行更快。Apriori算法產生候選項集，然後掃描數據集來檢查他們是否頻繁。由於只對數據集掃描兩次，因此FP-growth算法執行更快。在FP-growth算法中，數據集存儲在一個稱為FP樹的結構中。FP樹構建完成後，可以通過查找元素項的條件及FP樹來發現頻繁項集。該過程不斷以更多元素作為條件重復進行，直到FP樹只包含一個元素為止。

機器學習的9個基礎概念和10種基本算法總結