題目描述

如題，已知一個數列，你需要進行下面兩種操作：

1.將某區間每一個數數加上x

2.求出某一個數的和

輸入輸出格式

輸入格式：

第一行包含兩個整數N、M，分別表示該數列數字的個數和操作的總個數。

第二行包含N個用空格分隔的整數，其中第i個數字表示數列第i項的初始值。

接下來M行每行包含2或4個整數，表示一個操作，具體如下：

操作1： 格式：1 x y k 含義：將區間[x,y]內每個數加上k

操作2： 格式：2 x 含義：輸出第x個數的值

輸出格式：

輸出包含若幹行整數，即為所有操作2的結果。

輸入輸出樣例

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

6
10

說明

時空限制：1000ms,128M

數據規模：

對於30%的數據：N<=8，M<=10

對於70%的數據：N<=10000，M<=10000

對於100%的數據：N<=500000，M<=500000

樣例說明：

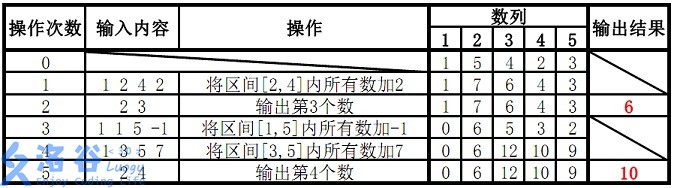
故輸出結果為6、10

思路 ：

本題用到的思想是差分，通過樹狀數組可以快速地進行修改、查詢

設數組a[]={1,6,8,5,10}，那麽差分數組b[]={1,5,2,-3,5}

也就是說b[i]=a[i]-a[i-1];(a[0]=0;)，那麽a[i]=b[1]+....+b[i];(這個很好證的)。

假如區間[2,4]都加上2的話

a數組變為a[]={1,8,10,7,10}，b數組變為b={1,7,2,-3,3};

發現了沒有，b數組只有b[2]和b[5]變了，因為區間[2,4]是同時加上2的,所以在區間內b[i]-b[i-1]是不變的.

所以對區間[x,y]進行修改,只用修改b[x]與b[y+1]:

b[x]=b[x]+k;b[y+1]=b[y+1]-k;

代碼：

#include<stdio.h>
#define ll long long 
#define lowbit(x) x&-x
using namespace std;
const int MX=500001;
int n,m,dif[MX];

void add(int x,int num)
{
    while(x<=n)
    {
        dif[x]
 
+=num;    
        x+=lowbit(x);
    }
}

ll qur(int x)
{
    ll ans=0;
    while(x)
    {
        ans+=dif[x];
        x-=lowbit(x);
    }
    return ans;
}

int main()
{
    scanf("%d%d",&n,&m);
    int last=0;
    for(int i=1;i<=n;++i) {
        int x;
        scanf("%d",&x);
        add(i,x-last);
        last=x;
    }
    while(m--) 
    {
        int cas;
        scanf("%d",&cas);
        if(cas==1) 
        {
            int l,r,num;
            scanf("%d%d%d",&l,&r,&num);
            add(l,num);
            add(r+1,-num);
            
        }
        else if(cas==2)
        {
            int x;
            scanf("%d",&x);
            printf("%lld\n",qur(x));
        }
    }
    return 0;
}

更新區間，求單點—— luogu 3368