前言

眼看著聯賽將近，周圍的大佬們都開始學起了splay等高級數據結構算法，蒟蒻的我只好學一學treap,咦！？竟然有一種treap可以支持區間操作（splay）還那麽友好碼量適中？！小蒟蒻趕緊來安利一波

• 簡介

  fhq_treap是一位名叫fhq的大佬想出來的（這不廢話嗎），它是基於treap的基礎上加以優化得出的算法（這也是句廢話），treap就是二叉搜索樹加上堆，它每次進行一次操作（插入或刪除等）都要經過左右旋轉來維護二叉搜索樹的平衡，每次都旋轉一次好麻煩有木~，於是乎，為了科技的創新偷懶fhq大佬創作出了這樣一個算法，大大減少了代碼復雜度，也讓fhq_treap可以很輕易的完成區間上的操作！！造福（像我一樣懶的

  ）人類呀

好我們來進入正題；

為什麽fhq_treap能完成如此多的操作還碼量適中呢？ 一切都得益於兩個神奇的操作 merge 和 split。 顧名思義，一個是將兩顆treap樹合並為一顆，一個是將一顆treap樹分裂成兩顆treap樹。

1. merge

int merge(int x,int y){
    if(!x || !y) return x+y;//如果有一顆為空，那麽只要返回不為空的那一顆就行了
    if(rd[x]<rd[y]){   //treap的做法，比較他們的優先值
        ch[x][1]=merge(ch[x][1],y); 
        up(x);return x; // 將x的右子樹與y合並為一顆，那麽目前的x就是合並後的樹
    }
    else{
        ch[y][0]=merge(x,ch[y][0]);
        up(y);return y;//反之亦然
    }
}
 

2.split

void split(int now,int k,int &x,int &y){//意思是將now樹，以k為分割點（大於k在右邊，小於K在左邊），分為x,y兩棵樹
    if(!now) x=y=0;//如果now 樹為空，那麽x,y樹都為空.
    else{
        if(val[now]<=k){
            x=now,split(ch[now][1],k,ch[now][1],y);
        }
        else 
           y=now,split(ch[now][0],k,x,ch[now][0]);
        up(now);
    }
} 
 

好了，兩個基本操作講完了，那麽他有什麽用？

以這兩個操作為基礎，就可以解決其他操作啦~

先看看插入

insert

int insert(int &root,int x){//原樹是root，要插入x這個點
    int a,b;
    int v=val[x];
    split(root,v,a,b);
    root=marge(marge(a,x),b);
}

如果看不懂代碼可以看看圖。

這是一顆treap樹，右邊為要插入的點。

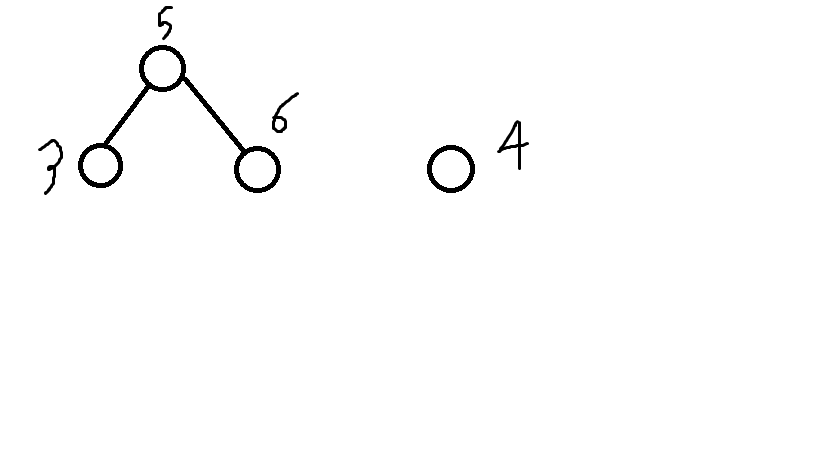
我們先把原樹按要插入這個點的值分為兩顆樹

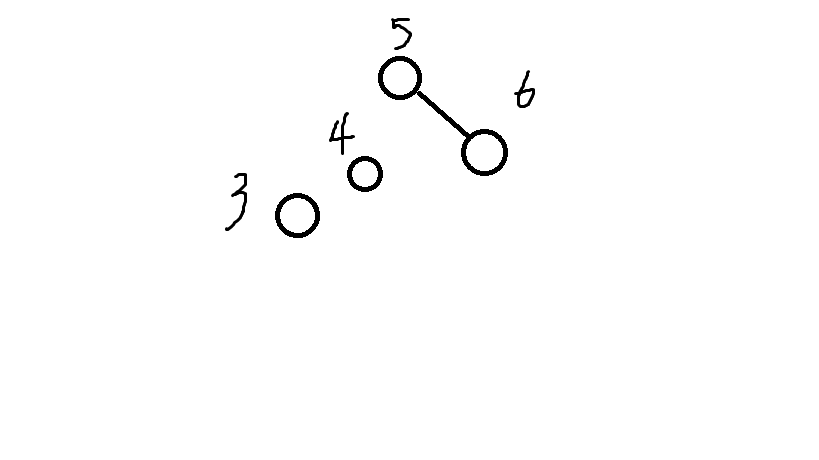
然後再要插入的點和小於他的那顆樹連起來

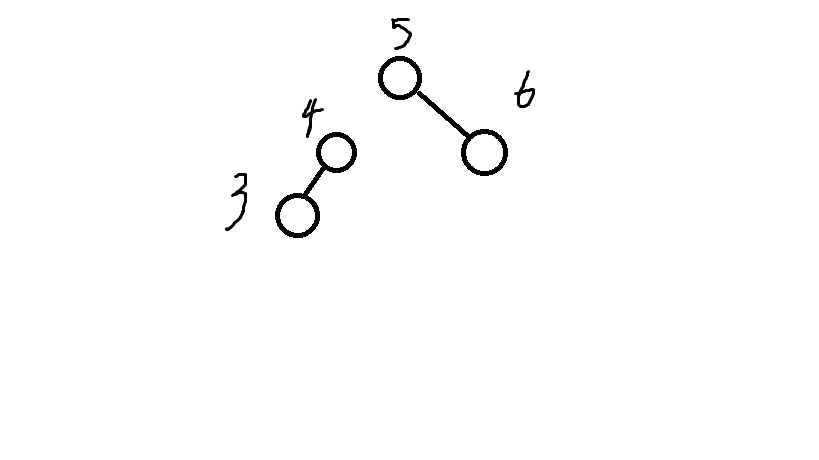
最後只需將這顆樹與大於他的這顆樹連起來就行了

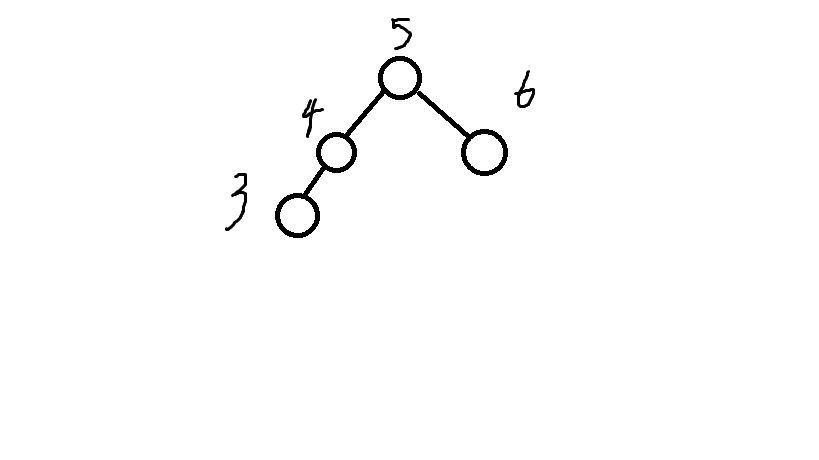
insert就講完了。

繼續挖坑以後有時間填

蒟蒻的學習筆記——平衡樹之FHQ_treap