---恢復內容開始---

2018研究生數學建模競賽B題-光傳送網建模與價值評估-競賽總結

這道賽題是有關通信方面的賽題,初步讀題,感到第一問和第二問關系不大,第二問和第三問關系也不大,不過第一問和第三問有比較緊密的順承關系.

1-1

第一問主要討論在光纖通信環境下,與光信號傳輸有關的調制解調的誤碼率問題.在題設條件中,糾前誤碼率(BER)只與信噪比(SNR)有關.因此題目要求我們建立數學模型描述兩者的關系.

對於該問題有兩種思路:

1. 建立機理模型

也就是通過對光纖中的入纖信號,與信號噪聲進行概率描述,然後推導出出纖信號的概率描述,從而通過對概率密度函數的二重積分,直接計算出兩者的解析關系.

1. 實驗模型

也就是使用計算機仿真的方式,通過大量的實驗,模擬信號輸入,編碼,噪聲輸入,解碼,計算誤碼率的過程,對誤碼率進行計算.根據大數定律,大量實驗的結果會趨近於第一種思路的機理模型的解.

1. 兩種方法的比較

第一種方法有著更強的數學要求,但是推到的結果顯示,最後的結果是一個正態分布函數的二重積分的加權和.計算這個函數的積分其實十分困難,還是要借助數值計算的工具或者查表.無法有效的得到一條表達式.

第二種方法較容易實現,但是在試驗次數較小的情況下,得到的曲線會引入較大誤差.造成求解曲線的不平滑.因此得到平滑的曲線需要花費較大的計算時間.在我的電腦上計算時間大概有半個小時.

在這裏給出一張求解圖.

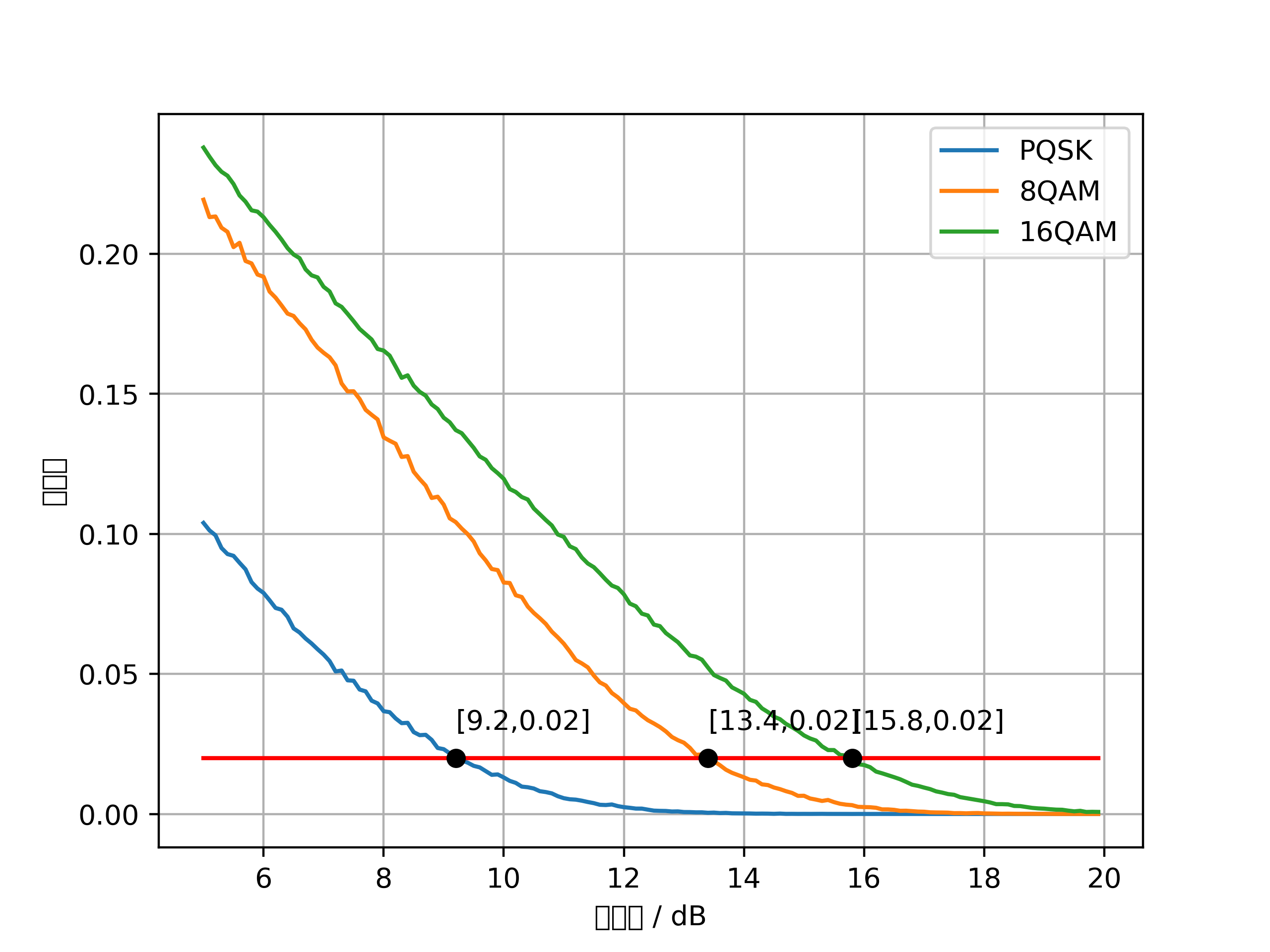
1-2

第二問主要是對整個傳輸的光路進行建模,要考慮光在線纜中引入的噪聲,光放大器引入的噪聲,光在線纜中的功率衰減等因素,結合上文中算出的一個參數求解傳輸鏈路的段數.

在這裏給出模型和結果.

結果

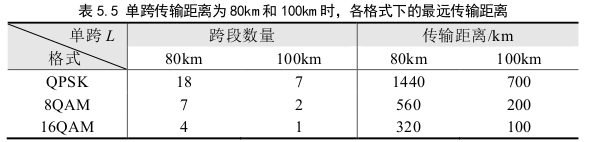
2-1

第二問似乎與第一問沒有必然的聯系,這是一個整數規劃的問題,特別是在第一問中,這個證書規劃非常的純粹,因此可以直接建立整數規劃的模型,使用相應的求解器進行求解.

我們將問題直接轉化成了MIP問題,然後使用GUROBI工具進行求解.

轉化成的問題如下圖.

其中Cij 表示 i 節點與 j 節點之間的傳輸容量,可依據節點間的距離選擇相應的傳輸格式,從而判斷傳輸容量的大小。本文認為,若要使網絡價值最大化,必須要以容量利用率最大為標準來分配傳輸格式。

λ ij 表示 i 節點與 j 節點之間鏈路的權重,M 為光傳輸網絡的節點數。
H i ,H j 分別表示 i 節點和 j 節點的人口數。當所有節點的鏈接情況由決策
信息R ij 確定時,目標函數值中相應的未知變量可進一步求出並確定目標函數值.

約束中限制了網絡連接數,和孤立鏈路數量.

值得一題的是孤立鏈路這個約束.

在一開始我們解出的解如下圖:

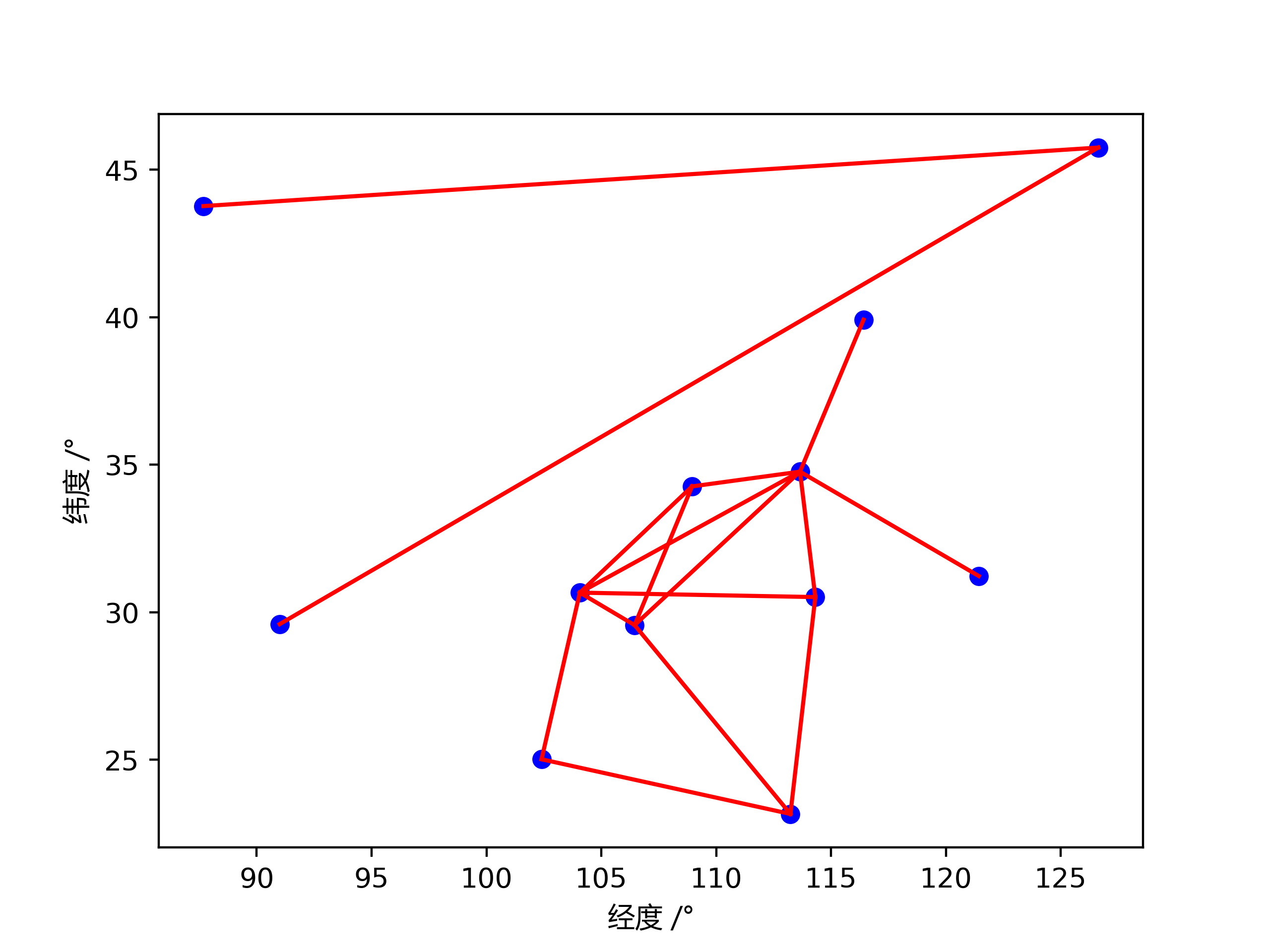
可以看到,得到的解並不是一個連通的圖.但是作為一個光纖網絡來說,必然要求我們解出一個連通圖.因此我們加入了孤立鏈路這個新的約束.

這個約束可以保證所有組成的集合(全集和空集除外)都與其他點是連通的.加入當前約束後得到的解如下圖所示.

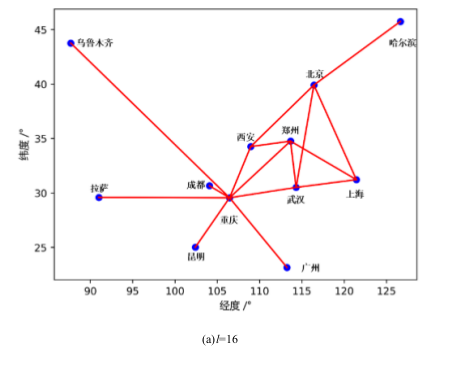
對於33條鏈路的是這樣的.

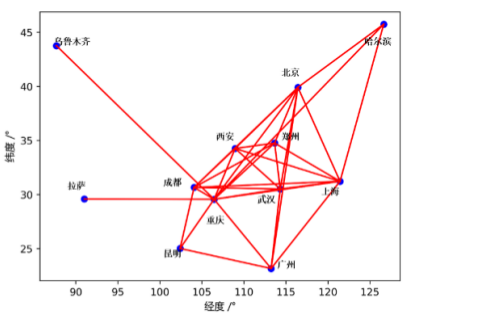
2-2

第二問考慮到中轉節點的問題,最初考慮在第一問的基礎上進行拓展,為每條路段增加一個分配變量,也就是在這些變量中描述當前路段的資源是否進行分配,分配給誰.

然後通過增加約束條件約束分配必須滿足題設需求.但是求解過程發現這樣的求解占用太多資源.因此我們考慮將問題轉化成為了一個層次優化的問題.在描述這個問題前,我們通過一些數學推導將問題稍作簡化.

首先,中轉通信的可行性分析.

一條線路進行中轉的可行性,主要是由引入這些中轉是否會帶來目標(網絡價值)的提升判斷的.
如果引入這些中轉可以將網絡價值進行提升,那麽系統將義不容辭的引入這些中轉通信,如果不能,中轉通信將一定不會被引入.

因此在引入的價值該如何度量呢?

看下圖:

也就是說,當權重保持不變的情況下. 引入中轉通信完全歸結為節點的人口問題,對於三個節點的判斷來說.當中間點城市的人口數足夠小的情況下,引入中間節點通信是有好處的.

下面我們來進行更加復雜的分析.

當有多個城市需要占用同一個節點中轉時,節點將為哪一個城市服務的問題.這個問題同樣該從網絡價值的角度分析.就是說我們要比較為誰服務可以獲得更多的網絡價值.

但是這個問題就沒有前面的問題那樣純粹了,因為這將變成一個整體性的問題.也是一個規劃問題.為了有效解決這個問題,本文件問題描述為一個兩層的最優化問題的嵌套.

頂層的最優化問題負責尋找最優的網絡路徑,也就是像問題2-1一樣的規劃問題.第二個最優化問題在上層給出的路徑的基礎上尋找一個最優化的網絡配置,配置最優化的中轉節點情況.

在這種情況下,我們本文采用兩層的架構,第一層使用遺傳算法作為框架,第二層使用約束式求解器GUROBI.

2-3 第三問是自由式的問題,因此在這裏不做分享

3

第三問由於太直接,沒有太好的方法進行求解,所以直接上了遺傳算法.
沒有什麽有效的數學模型可以將問題化簡,大家有興趣可以直接看我的代碼.

代碼:

問題求解的正確性我還沒有作進一步的考證,
在這裏發表一些想法只做討論用.
代碼我已經上傳到了github: https://github.com/zangzelin/2018-Graduate-Mathematical-Modeling-Competition-B
希望覺得有幫助的同學,star 一下

---恢復內容結束---

這道賽題是有關通信方面的賽題,初步讀題,感到第一問和第二問關系不大,第二問和第三問關系也不大,不過第一問和第三問有比較緊密的順承關系.

1-1

第一問主要討論在光纖通信環境下,與光信號傳輸有關的調制解調的誤碼率問題.在題設條件中,糾前誤碼率(BER)只與信噪比(SNR)有關.因此題目要求我們建立數學模型描述兩者的關系.

對於該問題有兩種思路:

1. 建立機理模型

也就是通過對光纖中的入纖信號,與信號噪聲進行概率描述,然後推導出出纖信號的概率描述,從而通過對概率密度函數的二重積分,直接計算出兩者的解析關系.

1. 實驗模型

也就是使用計算機仿真的方式,通過大量的實驗,模擬信號輸入,編碼,噪聲輸入,解碼,計算誤碼率的過程,對誤碼率進行計算.根據大數定律,大量實驗的結果會趨近於第一種思路的機理模型的解.

1. 兩種方法的比較

第一種方法有著更強的數學要求,但是推到的結果顯示,最後的結果是一個正態分布函數的二重積分的加權和.計算這個函數的積分其實十分困難,還是要借助數值計算的工具或者查表.無法有效的得到一條表達式.

第二種方法較容易實現,但是在試驗次數較小的情況下,得到的曲線會引入較大誤差.造成求解曲線的不平滑.因此得到平滑的曲線需要花費較大的計算時間.在我的電腦上計算時間大概有半個小時.

在這裏給出一張求解圖.

1-2

第二問主要是對整個傳輸的光路進行建模,要考慮光在線纜中引入的噪聲,光放大器引入的噪聲,光在線纜中的功率衰減等因素,結合上文中算出的一個參數求解傳輸鏈路的段數.

在這裏給出模型和結果.

結果

2-1

第二問似乎與第一問沒有必然的聯系,這是一個整數規劃的問題,特別是在第一問中,這個證書規劃非常的純粹,因此可以直接建立整數規劃的模型,使用相應的求解器進行求解.

我們將問題直接轉化成了MIP問題,然後使用GUROBI工具進行求解.

轉化成的問題如下圖.

其中Cij 表示 i 節點與 j 節點之間的傳輸容量,可依據節點間的距離選擇相應的傳輸格式,從而判斷傳輸容量的大小。本文認為,若要使網絡價值最大化,必須要以容量利用率最大為標準來分配傳輸格式。

λ ij 表示 i 節點與 j 節點之間鏈路的權重,M 為光傳輸網絡的節點數。
H i ,H j 分別表示 i 節點和 j 節點的人口數。當所有節點的鏈接情況由決策
信息R ij 確定時,目標函數值中相應的未知變量可進一步求出並確定目標函數值.

約束中限制了網絡連接數,和孤立鏈路數量.

值得一題的是孤立鏈路這個約束.

在一開始我們解出的解如下圖:

可以看到,得到的解並不是一個連通的圖.但是作為一個光纖網絡來說,必然要求我們解出一個連通圖.因此我們加入了孤立鏈路這個新的約束.

這個約束可以保證所有組成的集合(全集和空集除外)都與其他點是連通的.加入當前約束後得到的解如下圖所示.

對於33條鏈路的是這樣的.

2-2

第二問考慮到中轉節點的問題,最初考慮在第一問的基礎上進行拓展,為每條路段增加一個分配變量,也就是在這些變量中描述當前路段的資源是否進行分配,分配給誰.

然後通過增加約束條件約束分配必須滿足題設需求.但是求解過程發現這樣的求解占用太多資源.因此我們考慮將問題轉化成為了一個層次優化的問題.在描述這個問題前,我們通過一些數學推導將問題稍作簡化.

首先,中轉通信的可行性分析.

一條線路進行中轉的可行性,主要是由引入這些中轉是否會帶來目標(網絡價值)的提升判斷的.
如果引入這些中轉可以將網絡價值進行提升,那麽系統將義不容辭的引入這些中轉通信,如果不能,中轉通信將一定不會被引入.

因此在引入的價值該如何度量呢?

看下圖:

也就是說,當權重保持不變的情況下. 引入中轉通信完全歸結為節點的人口問題,對於三個節點的判斷來說.當中間點城市的人口數足夠小的情況下,引入中間節點通信是有好處的.

下面我們來進行更加復雜的分析.

當有多個城市需要占用同一個節點中轉時,節點將為哪一個城市服務的問題.這個問題同樣該從網絡價值的角度分析.就是說我們要比較為誰服務可以獲得更多的網絡價值.

但是這個問題就沒有前面的問題那樣純粹了,因為這將變成一個整體性的問題.也是一個規劃問題.為了有效解決這個問題,本文件問題描述為一個兩層的最優化問題的嵌套.

頂層的最優化問題負責尋找最優的網絡路徑,也就是像問題2-1一樣的規劃問題.第二個最優化問題在上層給出的路徑的基礎上尋找一個最優化的網絡配置,配置最優化的中轉節點情況.

在這種情況下,我們本文采用兩層的架構,第一層使用遺傳算法作為框架,第二層使用約束式求解器GUROBI.

2-3 第三問是自由式的問題,因此在這裏不做分享

3

第三問由於太直接,沒有太好的方法進行求解,所以直接上了遺傳算法.
沒有什麽有效的數學模型可以將問題化簡,大家有興趣可以直接看我的代碼.

代碼:

問題求解的正確性我還沒有作進一步的考證,
在這裏發表一些想法只做討論用.
代碼我已經上傳到了github: https://github.com/zangzelin/2018-Graduate-Mathematical-Modeling-Competition-B
希望覺得有幫助的同學,star 一下

2018研究生數學建模競賽B題-光傳送網建模與價值評估-競賽總結