賞月齋源碼共享計劃 第四期 約瑟夫問題
約瑟夫問題求解及優化
問題描述
在一間房間總共有n個人,給定一個數k,然後按照如下規則去殺人:
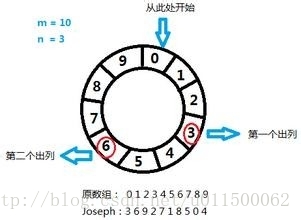
- 所有人圍成一個圓圈,按順時針依次給所有人編號:1, 2, 3…, n
- 由編號1開始報數,按順時針方向,報到數字k的人將被殺掉
- 被殺掉的人從房間內被移走,從被殺的下一個人重新由1開始報數
- 報到數字k的人再次被殺掉,再移走,再次開始報數,一直殺到最後剩余一個人
最後剩余的人活命。
那麽,給定了 n 和 k,最後活下來的人的編號是幾?
思路一
根據問題描述,可以使用循環單鏈表模擬殺人過程:
- 表頭是1號,表尾是n號,循環單鏈表的表尾指向表頭模擬圓圈
- 指針從表頭1號開始走,當指到第k個節點時,即當報k的被殺時,就將該節點從鏈表中刪除。
- 刪除該節點後,從該節點的下一個節點開始,再從1走到k,
- 再次刪除第k節點,一直到某節點的下一個節點指向自己,說明只有一個節點了,即最後活下的人
根據上面分析循環單鏈表的操作過程,代碼實現如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
class Node(object):
def __init__(self, value): |
這種方法的時間復雜度為:O(n*k),當人數量n很大,報的數k也很大時,並不適用。
思路二
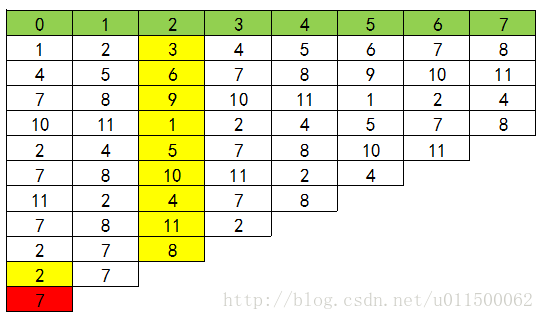
遞歸思路,假設房間共有n = 10個人,初始編號為1,2,3,…10,設初始編號對應的編號位置為0, 1, 2, …9, 每次數到k = 3的人殺死,求最後活下來的人的初始編號是幾?
來看殺人過程:
 約瑟夫問題遞歸思路求解過程
約瑟夫問題遞歸思路求解過程
(表中紅色為報數k=3的被殺死的人的編號,綠色為最後活下來的人的編號)
仔細觀察表中每一輪初始編號的移動規律:
第二輪到第一輪的編號移動規律: (第二輪的編號x的編號位置 + k) % 10 ==> 第一輪編號x的編號位置
比如第二輪編號5的編號位置是1, (1 + 3) % 10 ==> 4, 得到第一輪編號5的的編號位置是4
進而得到第三輪到第二輪的編號移動規律:(第三輪編號x的編號位置 + k) % 9 ==> 第二輪編號x的編號位置
比如第三輪編號5的編號位置是7, (7 + 3) % 9 –> 1, 得到第二輪編號5的的編號位置是1
進而得到第N輪與第N-1輪的編號移動規律:(第N輪的編號x的編號位置 + k) % 第N-1輪總人數 ==> 第N-1輪編號x的編號位置
最後一輪存活著的編號x對應的編號位置一定是0, 那麽根據以上規律,可以得到倒數第二輪編號x對應的編號位置,根據規律進一步可以得到倒數第三輪編號x對應的編號位置, 一直可以推導出第一輪編號x的對應編號位置,由第一輪編號x的對應編號位置+1得到的便是最後存活的人的初始編號。
由上總結,當房間共有n個人,報數k殺死時,令f(n, k)表示最後存活著的編號位置,則有遞歸公式:
- n = 1: f(1, k) = 0;
- n > 1: f(n, k) = (f(n-1, k) + k) % n;
有了遞推公式以後,代碼實現如下:
| 1 2 3 4 5 6 7 8 9 | def josephus(n, k): if n == 1: return 0 else: return (josephus(n - 1, k) + k) % n n = 10 k = 3 print("最後存活者編號是:", josephus(n, k)+1) # 4 |
對思路二的優化
對遞歸思路的進一步優化,假設n非常大,而k又比較小,比如n=100, k=3, 被殺過程如下:
- 第一輪: 有100個人,每次報k=3的被殺,總共殺死了 math.floor(100/3) = 33個人,剩余67個人
- 第二輪: 有67個人,每次報k=3的被殺,總共殺死了 math.floor(67/3) = 22個人,剩余45個人
- 第三輪: 有45個人,每次報k=3的被殺,總共殺死了 math.floor(45/3) = 15個人,剩余30個人
- 第四輪: 有30個人,每次報k=3的被殺,總共殺死了 math.floor(30/3) = 10個人,剩余20個人
- 第五輪: 有20個人,每次報k=3的被殺,總共殺死了 math.floor(20/3) = 6個人,剩余14個人
- 第六輪: 有14個人,每次報k=3的被殺,總共殺死了 math.floor(14/3) = 4個人,剩余10個人
- 第七輪: 有10個人,每次報k=3的被殺,總共殺死了 math.floor(10/3) = 3個人,剩余7個人
- 第八輪: 有7個人,每次報k=3的被殺,總共殺死了 math.floor(7/3) = 2個人,剩余5個人
- 第九輪: 有5個人,每次報k=3的被殺,總共殺死了 math.floor(5/3) = 1個人,剩余4個人
- 第十輪: 此時,總人數n=4, 報的數k=3,再利用思路二中的遞歸方法求解最後剩余者編號
在上面殺人過程中,通過建立n/k的步長加快了殺人的速度,減少了算法時間。可以從下面這幅圖中更加清晰的體會到:
 約瑟夫問題遞歸思路求解過程優化
約瑟夫問題遞歸思路求解過程優化
本來需要10輪的,現在只需要7輪,如果n=100,k=3的話優化效果會更明顯。
根據以上分析,優化方法如下:
- math.floor(n/k) == 1: 用思路二中方法求解
- math.floor(n/k) > 1: n = n - math.floor(n/k)
實現代碼:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | import math def josephus(n, k): if n == 1: return 0 else: return (josephus(n - 1, k) + k) % n def kill_people(n, k): while math.floor(n/k) > 1: # 建立一個步長為n/k的遞歸過程; n = n - math.floor(n/k) kill_people(n, k) live_index = josephus(n, k) return live_index+1 n = 10 k = 3 print("最後存活者編號是", kill_people(n,k)) |
思路三
使用數組存儲房間中的每個人: arr = [ i for i in range(1, 10+1) ]
arr數組代表房間裏的10個人:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
每次被殺的人的編號: kill_num = (kill_num + k - 1) % len(arr)。 其中的(k-1)對應數組的下標
有了被殺人的的編號後,將其pop出數組。
然後再次計算下一個被殺人的編號,直到數組中只剩一個人。
代碼實現:
| 1 2 3 4 5 6 7 8 9 10 11 12 | def josephus(n, k): arr = [ i for i in range(1, n+1) ] kill_num = 0 while len(arr) != 1: kill_num = (kill_num + k - 1) % len(arr) print("殺死:" + str(arr.pop(kill_num))) return arr[0] n = 10 k = 3 print("最後存活者編號是:", josephus(n, k)) # 4 |
對思路三的優化
在思路三中需要構建一個數組,也可以不用數組來減少內存。使用動態規劃來解:
| 1 2 3 4 5 6 7 8 9 | def Josephus(n, k): kill_num = 0 for i in range(1, n+1): kill_num = (k + kill_num) % i return kill_num + 1 n = 5 k = 2 print("最後存活者編號:", Josephus(n, k)) |
最後這個動態規劃的方法來自:https://www.quora.com/What-is-the-best-solution-for-Josephus-problem-algorithm
約瑟夫問題
約瑟夫問題是個著名的問題:N個人圍成一圈,第一個人從1開始報數,報M的將被殺掉,下一個人接著從1開始報。如此反復,最後剩下一個,求最後的勝利者。
例如只有三個人,把他們叫做A、B、C,他們圍成一圈,從A開始報數,假設報2的人被殺掉。
- 首先A開始報數,他報1。僥幸逃過一劫。
- 然後輪到B報數,他報2。非常慘,他被殺了
- C接著從1開始報數
- 接著輪到A報數,他報2。也被殺死了。
- 最終勝利者是C
解決方案
普通解法
剛學數據結構的時候,我們可能用鏈表的方法去模擬這個過程,N個人看作是N個鏈表節點,節點1指向節點2,節點2指向節點3,……,節點N-1指向節點N,節點N指向節點1,這樣就形成了一個環。然後從節點1開始1、2、3……往下報數,每報到M,就把那個節點從環上刪除。下一個節點接著從1開始報數。最終鏈表僅剩一個節點。它就是最終的勝利者。
缺點:
要模擬整個遊戲過程,時間復雜度高達O(nm),當n,m非常大(例如上百萬,上千萬)的時候,幾乎是沒有辦法在短時間內出結果的。
公式法
約瑟夫環是一個經典的數學問題,我們不難發現這樣的依次報數,似乎有規律可循。為了方便導出遞推式,我們重新定義一下題目。
問題: N個人編號為1,2,……,N,依次報數,每報到M時,殺掉那個人,求最後勝利者的編號。
這邊我們先把結論拋出了。之後帶領大家一步一步的理解這個公式是什麽來的。
遞推公式:
- f(N,M)f(N,M)表示,N個人報數,每報到M時殺掉那個人,最終勝利者的編號
- f(N−1,M)f(N−1,M)表示,N-1個人報數,每報到M時殺掉那個人,最終勝利者的編號
下面我們不用字母表示每一個人,而用數字。
表示11個人,他們先排成一排,假設每報到3的人被殺掉。
- 剛開始時,頭一個人編號是1,從他開始報數,第一輪被殺掉的是編號3的人。
- 編號4的人從1開始重新報數,這時候我們可以認為編號4這個人是隊伍的頭。第二輪被殺掉的是編號6的人。
- 編號7的人開始重新報數,這時候我們可以認為編號7這個人是隊伍的頭。第三輪被殺掉的是編號9的人。
- ……
- 第九輪時,編號2的人開始重新報數,這時候我們可以認為編號2這個人是隊伍的頭。這輪被殺掉的是編號8的人。
- 下一個人還是編號為2的人,他從1開始報數,不幸的是他在這輪被殺掉了。
- 最後的勝利者是編號為7的人。
下圖表示這一過程(先忽視綠色的一行)
現在再來看我們遞推公式是怎麽得到的!
將上面表格的每一行看成數組,這個公式描述的是:幸存者在這一輪的下標位置
- f(1,3)f(1,3):只有1個人了,那個人就是獲勝者,他的下標位置是0
- f(2,3)=(f(1,3)+3)%2=3%2=1f(2,3)=(f(1,3)+3)%2=3%2=1:在有2個人的時候,勝利者的下標位置為1
- f(3,3)=(f(2,3)+3)%3=4%3=1f(3,3)=(f(2,3)+3)%3=4%3=1:在有3個人的時候,勝利者的下標位置為1
- f(4,3)=(f(3,3)+3)%4=4%4=0f(4,3)=(f(3,3)+3)%4=4%4=0:在有4個人的時候,勝利者的下標位置為0
- ……
- f(11,3)=6f(11,3)=6
很神奇吧!現在你還懷疑這個公式的正確性嗎?上面這個例子驗證了這個遞推公式的確可以計算出勝利者的下標,下面將講解怎麽推導這個公式。
問題1:假設我們已經知道11個人時,勝利者的下標位置為6。那下一輪10個人時,勝利者的下標位置為多少?
答:其實吧,第一輪刪掉編號為3的人後,之後的人都往前面移動了3位,勝利這也往前移動了3位,所以他的下標位置由6變成3。
問題2:假設我們已經知道10個人時,勝利者的下標位置為3。那下一輪11個人時,勝利者的下標位置為多少?
答:這可以看錯是上一個問題的逆過程,大家都往後移動3位,所以f(11,3)=f(10,3)+3f(11,3)=f(10,3)+3。不過有可能數組會越界,所以最後模上當前人數的個數,f(11,3)=(f(10,3)+3)%11f(11,3)=(f(10,3)+3)%11
問題3:現在改為人數改為N,報到M時,把那個人殺掉,那麽數組是怎麽移動的?
答:每殺掉一個人,下一個人成為頭,相當於把數組向前移動M位。若已知N-1個人時,勝利者的下標位置位f(N−1,M)f(N−1,M),則N個人的時候,就是往後移動M為,(因為有可能數組越界,超過的部分會被接到頭上,所以還要模N),既f(N,M)=(f(N−1,M)+M)%nf(N,M)=(f(N−1,M)+M)%n
註:理解這個遞推式的核心在於關註勝利者的下標位置是怎麽變的。每殺掉一個人,其實就是把這個數組向前移動了M位。然後逆過來,就可以得到這個遞推式。
因為求出的結果是數組中的下標,最終的編號還要加1
下面給出代碼實現:
int cir(int n,int m)
{
int p=0;
for(int i=2;i<=n;i++)
{
p=(p+m)%i;
}
return p+1;
}賞月齋源碼共享計劃 第四期 約瑟夫問題