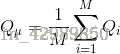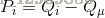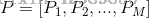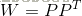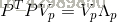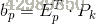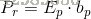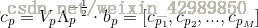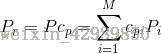文獻閱讀002【精讀】
2002 ICIP Face photo recognition using sketch
網盤鏈接 密碼:if7l
- ABSTRACT
- INTRODUCTION
- SKETCH RECOGNITION
2.1 Conventional eigenface method
2.2 Eigensketch transformation - EXPERIMENTS
- SUMMARY
2.1. Conventional eigenface method
Eigenface method是人臉識別的有效方法之一,它在FERET(人臉數據庫) test中表現出良好。
該方法使用KLT(Karhunen-Loeve Transform)來提取人臉的代表特征,該方法也叫PCA方法。
PCA算法:
輸入:樣本集D={x1,x2,...,xm}, 低維維數k
過程:
1.數據中心化/歸一化: xi = xi - μi
2.計算協方差矩陣: XX^T
3.對XX^T做奇異值分解
4.取前k個最大的特征值對應的特征向量w1,w2,...,wk
輸出:投影矩陣W={w1,w2,...,wk}
Qi 表示一張圖像的向量(column vector),Qu 表示平均值,以下為中心化/歸一化:
P 為所有樣本向量歸一化後合起來(訓練集)的矩陣,W 為協方差矩陣(covariance matrix):
經過奇異值分解(SVD)得到 特征向量組成的矩陣Vp, 特征值組成的對角矩陣Λp。
這裏有個地方要【註意】:由於W為N階矩陣(N為圖像的像素總數,即 Pi 的長度),對其直接進行SVD的話,計算量太大。因此我們可以先對W的轉置SVD,由於P為NxM的矩陣,M為向量個數(即訓練及大小),M<<N,所以計算量大大降低。
兩邊同時左乘P:
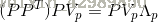
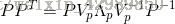
–求PPT的標準正交化矩陣:
–我們是先用SVD求出PTP標準正交化矩陣的,即Vp,Vp-1=VpT。而我們要求的是PPT的標準正交化矩陣,如上面的等式,我們不能保證PVp是標準正交化矩陣,因此要對其標準正交化,得到如下,可以驗證 EpEpT=I。
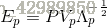
因此,對於一個新的圖片Pk,經過Ep的變換後,得到特征向量 bp :
2.2. Eigensketch transformation
對於上列等式,兩邊同時左乘Ep,由於Ep是標準正交矩陣,有Pk=Ep*bp,但是經過Ep降維後,這裏的等號實際上是有損失的,所以記Pk為Pr,即重構的photo:
將Ep代入:
–這裏的 cp 和Pk有什麽關系嗎?
–有。cp和bp有關,而 bp=Ep^TPk。
所以我們可以由樣本集原圖線性組合起來近似表示新的圖片的:
同理,我們把素描原始圖(sketch)也按這個線性組合重構:
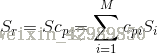
如圖2(Figure2),我們由(a)->(b)得到線性組合 cp,再用該線性組合(d)->(c).

3. EXPERIMENTS
用188對不同人臉的原始圖和素描圖(photo-sketch pairs)。
訓練集:88 photo-sketch pairs
測試集:100 photo-sketch pairs
同時,還設置三組不同方法進行比較,分別為:幾何法(geometry),傳統法(conventional),以及本論文的方法。
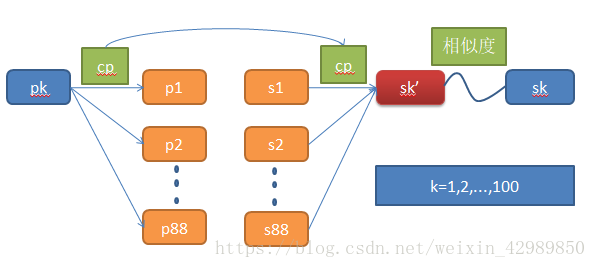
試驗采用 FERET test protocol(一種人臉識別算法評估方法),將測試集的photo作為gallery set,sketch作為probe set。計算相似度,如下表。
相似度計算過程:
從測試集的gallery set選取一張photo: Pk,用訓練集的88張photos來重構得到Pr,求出cp,再用cp來將訓練集中的sketches結合起來表示Sr’,最後與測試集的probe set中的sketches作比較,計算相似度。如下圖:
FERET Sep96 protocol 相關鏈接:
The_FERET_Verification_Testing_Protocol_for_Face_Recognition_Algorithms
文獻閱讀002【精讀】