[Codeforces Round #461 (Div2)] 題解
[比賽鏈接]
http://codeforces.com/contest/922
[題解]
Problem A. Cloning Toys
[算法]
當y = 0 , 不可以
當y = 1 , x不為0時 ， 不可以
當 y - 1 <= x , (x - y + 1)為偶數時 ， 可以
時間復雜度 : O(1)
[代碼]
#include<bits/stdc++.h> usingnamespace std; template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); } template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); } template <typename T> inline void read(T &x) { T f = 1; x = 0; char c = getchar(); for (; !isdigit(c); c = getchar()) if(c == ‘-‘) f = -f; for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - ‘0‘; x *= f; } int main() { int x , y; read(x); read(y); if (y == 0) printf("No\n"); else if (y == 1 && x != 0) printf("No\n"); else if (y - 1<= x && (x - y + 1) % 2 == 0) printf("Yes\n"); else printf("No\n"); return 0; }
Problem B. Magic Forest
[算法]
枚舉三角形的兩邊 ， 計算第三邊 ， 判斷是否能構成三角形即可
時間復雜度 : O(N^2)
[代碼]
#include<bits/stdc++.h> using namespace std; int n; template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); } template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); } template <typename T> inline void read(T &x) { T f = 1; x = 0; char c = getchar(); for (; !isdigit(c); c = getchar()) if (c == ‘-‘) f = -f; for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - ‘0‘; x *= f; } inline bool ok(int x,int y,int z) { return x > 0 && y > 0 && z > 0 && x <= n && y <= n && z <= n && x + y > z && x + z > y && y + z > x; } int main() { int answer = 0; read(n); for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { int k = i ^ j; if (ok(i,j,k)) answer++; } } answer /= 6; printf("%d\n",answer); return 0; }
Problem C. Cave Painting
[算法]
一個數除以1余數只可能為0
一個數除以2余數只可能為0,1
....
一個數除以n余數只可能為0,1,2,...n - 1
因此 ， 我們只需判斷對於i <= k , n除以i余數是否余數(i - 1)
時間復雜度 : O(K)
[代碼]
#include<bits/stdc++.h> using namespace std; typedef long long LL; template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); } template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); } template <typename T> inline void read(T &x) { T f = 1; x = 0; char c = getchar(); for (; !isdigit(c); c = getchar()) if (c == ‘-‘) f = -f; for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - ‘0‘; x *= f; } int main() { LL n , k; read(n); read(k); for (LL i = 1; i <= k; i++) { if (n % i != i - 1) { printf("No\n"); return 0; } } printf("Yes\n"); return 0; }
Problem D. Robot Vacuum Cleaner
[算法]
顯然 ， 答案只與字符串中"s"和"h"的個數有關
若a.s * b.h > a.h * b.s ， a比b優
調用std :: sort即可 ， 時間復雜度 ： O(NlogN)
[代碼]
#include<bits/stdc++.h> using namespace std; typedef long long LL; const int MAXN = 1e5 + 10; struct info { int s , h; } a[MAXN]; int n; inline bool cmp(info a,info b) { return 1ll * a.s * b.h > 1ll * b.s * a.h; } int main() { cin >> n; LL ans = 0; for (int i = 1; i <= n; i++) { string s; cin >> s; for (int j = 0; j < (int)s.size(); j++) { if (s[j] == ‘h‘) { a[i].h++; ans += a[i].s; } else a[i].s++; } } sort(a + 1,a + n + 1,cmp); int pre = 0; for (int i = 1; i <= n; i++) { ans += 1ll * pre * a[i].h; pre += a[i].s; } printf("%I64d\n",ans); return 0; }
Problem E. Birds
[算法]
註意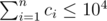 
.,考慮使用動態規劃
用f[i][j]表示在前i只小鳥中選j只 ， 最多還剩多少能量 , 轉移比較顯然 ， 不再贅述
時間復雜度 : O(NV)
[代碼]
#include<bits/stdc++.h> using namespace std; typedef long long LL; const LL MAXN = 1e3 + 10; const LL MAXS = 1e4 + 10; const LL inf = 1e18; LL n , W , B , X; LL c[MAXN],cost[MAXN]; LL dp[MAXN][MAXS]; template <typename T> inline void chkmax(T &x,T y) { x = max(x,y); } template <typename T> inline void chkmin(T &x,T y) { x = min(x,y); } template <typename T> inline void read(T &x) { T f = 1; x = 0; char c = getchar(); for (; !isdigit(c); c = getchar()) if (c == ‘-‘) f = -f; for (; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + c - ‘0‘; x *= f; } int main() { read(n); read(W); read(B); read(X); for (LL i = 1; i <= n; i++) read(c[i]); for (LL i = 1; i <= n; i++) read(cost[i]); for (LL i = 0; i <= n; i++) { for (LL j = 0; j < MAXS; j++) { dp[i][j] = -inf; } } LL cnt = c[1]; for (LL i = 0; i <= c[1]; i++) { if (W - 1LL * i * cost[1] >= 0) dp[1][i] = min(W - 1LL * i * cost[1] + X,W + i * B); else break; } for (LL i = 2; i <= n; i++) { cnt += c[i]; for (LL j = 0; j <= cnt; j++) { for (LL k = 0; k <= min(j,c[i]); k++) { if (dp[i - 1][j - k] == -inf) continue; if (dp[i - 1][j - k] - 1LL * cost[i] * k >= 0) chkmax(dp[i][j],min(1LL * W + 1LL * j * B,dp[i - 1][j - k] + 1LL * X - 1LL * cost[i] * k)); } } } LL ans = 0; for (LL i = 1; i <= cnt; i++) { if (dp[n][i] >= 0) ans = i; } printf("%I64d\n",ans); return 0; }
Problem F. Divisbility
[算法]
[Codeforces Round #461 (Div2)] 題解