去年冬天就接觸KMP算法了，但是聽的不明不白，遇到字符串匹配的題我大都直接使用string中的find解決了，但今天數據結構課又講了一下，我覺得有必要再來回顧一下。之前看過很多關於KMP的博客，有很多雖然很好，但是要麽太專業，要麽很難想象，這篇博客用了大量的圖示例子來說明，主要在於啟發，後面給出代碼說明。

主要參考：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

https://www.cnblogs.com/yjiyjige/p/3263858.html

KMP算法引入：

KMP是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同時發現的

KMP算法要解決的問題就是在字符串（也叫主串）中的模式（pattern）定位問題。說簡單點就是我們平時常說的關鍵字搜索。模式串就是關鍵字（接下來稱它為P），如果它在一個主串（接下來稱為T）中出現，就返回它的具體位置，否則返回-1（常用手段）。

首先，對於這個問題有一個很單純的想法：從左到右一個個匹配，如果這個過程中有某個字符不匹配，就跳回去，將模式串向右移動一位。這有什麽難的？

我們可以這樣初始化：

之後我們只需要比較i指針指向的字符和j指針指向的字符是否一致。如果一致就都向後移動，如果不一致，如下圖：

A和E不相等，那就把i指針移回第1位（假設下標從0開始），j移動到模式串的第0位，然後又重新開始這個步驟：

基於這個想法我們可以得到以下的程序：

 1 public static int bf(String ts, String ps)
 2 {
 3     int i = 0; // 主串的位置
 4     int j = 0; // 子串的位置
 5     while (i < t.length && j < p.length)
 6     {
 7         if (t[i] == p[j])/// 當兩個字符相同，就比較下一個
 8         {
 9             i++;
10             j++;
11
 
         }
12         else
13         {
14             i = i - j + 1;///一旦不匹配，i後退
15             j = 0; ///j歸0
16         }
17 
18     }
19     if (j == p.length)
20     {
21         return i - j;///匹配成功返回子串在母串最先出現的位置
22     }
23     else
24     {
25         return -1;///不成功返回-1
26     }
27 
28 }

然而這並不是一種優秀的算法，因為會出現指針的回退，一旦匹配不成功就要退回子串的其實位置，而之前完成的部分匹配也將作廢，時間復雜度為O（n*m）。

而KMP算法卻能將時間復雜度優化為O(n+m)，它是怎麽做到的呢？我們再舉一個例子。

（1）對於已經匹配到這種狀態的兩個字符串：

一個基本事實是，當空格與D不匹配時，你其實知道前面六個字符是"ABCDAB"。KMP算法的想法是，設法利用這個已知信息，不要把"搜索位置"移回已經比較過的位置，繼續把它向後移，這樣就提高了效率。

（2）

怎麽做到這一點呢？可以針對搜索詞，算出一張《部分匹配表》（Partial Match Table）。這張表是如何產生的，後面再介紹，這裏只要會用就可以了。

（3）

已知空格與D不匹配時，前面六個字符"ABCDAB"是匹配的。查表可知，最後一個匹配字符B對應的"部分匹配值"為2，因此按照下面的公式算出向後移動的位數：

移動位數 = 已匹配的字符數 - 對應的部分匹配值

因為 6 - 2 等於4，所以將搜索詞向後移動4位。

(4)

因為空格與Ｃ不匹配，搜索詞還要繼續往後移。這時，已匹配的字符數為2（"AB"），對應的"部分匹配值"為0。所以，移動位數 = 2 - 0，結果為 2，於是將搜索詞向後移2位。

(5)

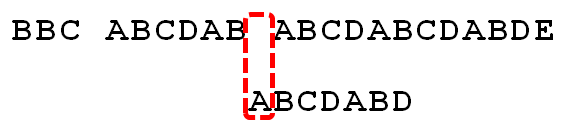
因為空格與A不匹配，繼續後移一位。

(6)

逐位比較，直到發現C與D不匹配。於是，移動位數 = 6 - 2，繼續將搜索詞向後移動4位。

(7)

逐位比較，直到搜索詞的最後一位，發現完全匹配，於是搜索完成。如果還要繼續搜索（即找出全部匹配），移動位數 = 7 - 0，再將搜索詞向後移動7位，這裏就不再重復了。

下面介紹《部分匹配表》是如何產生的。

首先，要了解兩個概念："前綴"和"後綴"。 "前綴"指除了最後一個字符以外，一個字符串的全部頭部組合；"後綴"指除了第一個字符以外，一個字符串的全部尾部組合。

"部分匹配值"就是"前綴"和"後綴"的最長的共有元素的長度。以"ABCDABD"為例，

－　"A"的前綴和後綴都為空集，共有元素的長度為0；
　　－　"AB"的前綴為[A]，後綴為[B]，共有元素的長度為0；
　　－　"ABC"的前綴為[A, AB]，後綴為[BC, C]，共有元素的長度0；
　　－　"ABCD"的前綴為[A, AB, ABC]，後綴為[BCD, CD, D]，共有元素的長度為0；
　　－　"ABCDA"的前綴為[A, AB, ABC, ABCD]，後綴為[BCDA, CDA, DA, A]，共有元素為"A"，長度為1；
　　－　"ABCDAB"的前綴為[A, AB, ABC, ABCD, ABCDA]，後綴為[BCDAB, CDAB, DAB, AB, B]，共有元素為"AB"，長度為2；
　　－　"ABCDABD"的前綴為[A, AB, ABC, ABCD, ABCDA, ABCDAB]，後綴為[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的長度為0。

為了記錄這些信息我們使用了一個next數組來記錄每一個字符的部分匹配值。

最後在對基本原理進行一下說明：

"部分匹配"的實質是，有時候，字符串頭部和尾部會有重復。比如，"ABCDAB"之中有兩個"AB"，那麽它的"部分匹配值"就是2（"AB"的長度）。搜索詞移動的時候，第一個"AB"向後移動4位（字符串長度-部分匹配值），就可以來到第二個"AB"的位置。這也是我認為KMP算法最為厲害的地方，利用字符串自身具有的重復性避免了指針的回退！！！

KMP字符串匹配算法