區塊鏈快速入門(六)——區塊鏈密碼學與安全相關技術
一、區塊鏈密碼安全技術簡介
區塊鏈和分布式賬本中大量使用了密碼學和安全技術的最新成果,特別是身份認證和隱私保護相關技術。區塊鏈使用了包括Hash 算法與摘要、加密算法、數字簽名和證書、PKI體系、Merkle 樹、布隆過濾器、同態加密等密碼安全相關技術,用於設計實現區塊鏈的機密性、完整性、可認證性和不可抵賴性。
二、Hash算法與數字摘要
1、Hash算法簡介
Hash(哈希或散列)算法,常被稱為指紋(fingerprint)或摘要(digest)算法,可以將任意長度的二進制明文串映射為較短的(通常是固定長度的)二進制串(Hash 值),並且不同的明文很難映射為相同的Hash值。
A、正向快速
給定原文和Hash算法,在有限時間和有限資源內能計算得到Hash值。
B、逆向困難
給定(若幹)Hash 值,在有限時間內無法(基本不可能)逆推出原文。
C、輸入敏感
原始輸入信息發生任何改變,新產生的Hash值都應該發生很大變化。
D、抗碰撞
很難找到兩段內容不同的明文,使得其Hash值一致(即發生碰撞)。
2、常見Hash算法
目前常見的Hash算法包括國際上的Message Digest(MD系列和Secure Hash Algorithm(SHA)系列算法以及國內的SM3算法。
MD算法主要包括MD4和MD5兩個算法。MD4(RFC 1320)是MIT的Ronald L.Rivest在 1990年設計的,其輸出為 128位。MD4已證明不夠安全。MD5(RFC 1321)是 Rivest於 1991年對MD4 的改進版本,對輸入仍以512位進行分組,其輸出是128位。MD5比MD4更加安全,但過程更加復雜,計算速度要慢一點。MD5 已於2004年被成功碰撞,其安全性已不足應用於商業場景。
中國密碼管理局於2010年12月17日發布了GM/T0004-2012《SM3密碼雜湊算法》,建立了國內商用密碼體系中的公開Hash算法標準,已經被廣泛應用在數字簽名和認證等場景中。
3、Hash算法的性能
大多數Hash算法都是計算敏感型算法,在強大的計算芯片上完成的更快。因此要提升Hash計算的性能可以考慮硬件加速。例如采用普通FPGA來計算SHA-256 值,可以輕易達到數Gbps 的吞吐量,使用專用芯片甚至會更高。
少數Hash算法不是計算敏感型的,如scrypt算法,其計算過程需要大量的內存資源,因此很難通過選用高性能芯片來加速Hash計算,可以有效防範采用專用芯片進行算力***。
4、數字摘要
數字摘要是Hash算法重要用途之一。數字摘要是對原始的數字內容進行Hash運算,獲取唯一的摘要值。
利用Hash函數抗碰撞性特點,數字摘要可以檢測內容是否被篡改過。
部分網站在提供文件下載時,會同時提供相應的數字摘要值。用戶下載原始文件後可以在本地自行計算摘要值,並與所提供摘要值進行比對,以確保文件內容沒有被篡改過。
5、Hash***與防護
Hash算法並不是一種加密算法,不能用於對信息的保護。但Hash算法可被應用到對登錄口令的保存上。例如網站登錄時需要驗證用戶名和密碼,如果網站後臺直接保存用戶的口令原文,一旦發生數據庫泄露後果不堪設想。
利用Hash的防碰撞特性,後臺數據庫可以僅保存用戶口令的Hash值,每次通過Hash值比對,即可判斷輸入口令是否正確。即便數據庫泄露,***者也無法輕易從Hash值還原回口令。
但如果用戶設置口令的安全強度不夠,采用了一些常見的字符串,如password、123456等。有人專門搜集常見口令,計算對應的Hash值,制作成字典,可以通過查看字典的Hash值可以快速反查到原始口令,如字典***和彩虹表***(只保存一條Hash鏈的首尾值,相對字典***可以節省存儲空間)等。
為了防範字典***、彩虹表***等***方法,可以采用加鹽(Salt)的方法。保存的不是原文的直接 Hash值,而是原文再加上一段隨機字符串(即“鹽”)後的Hash值。Hash結果和“鹽”分別存放在不同的地方,只要不是兩者同時泄,***者很難進行破解。
三、加解密算法
1、加解密系統簡介
加解密算法是現代密碼學核心技術,從設計理念和應用場景上可以分為兩大基本類型:對稱加密和非對稱加密。 
現代加解密系統的典型組件包括算法和密鑰(包括加密密鑰、解密密鑰)。其中,加解密算法自身是固定不變的,並且一般是公開可見的;密鑰則是最關鍵的信息,需要安全地保存起來,甚至通過特殊硬件進行保護。一般來說,密鑰需要在加密前按照特定算法隨機生成,長度越長,則加密強度越大。
加密過程中,通過加密算法和加密密鑰,對明文進行加密,獲得密文;解密過程中,通過解密算法和解密密鑰,對密文進行解密,獲得明文。
加解密的典型過程如下: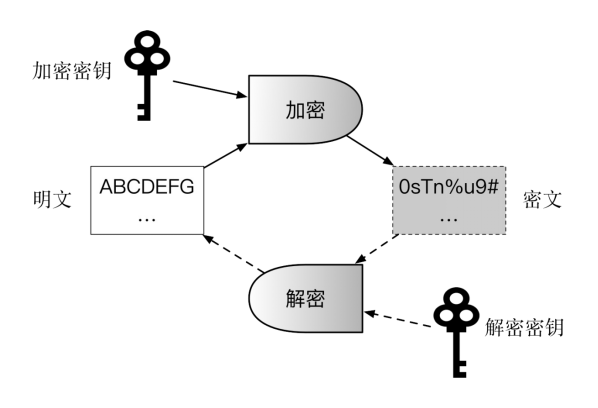
根據加解密過程中所使用的密鑰是否相同,算法可以分為對稱加密(Symmetric Cryptography)和非對稱加密(Asymmetric Cryptography)。兩種模式適用於不同的需求,形成互補。某些場景下可以組合使用,形成混合加密機制。
2、對稱加密算法
對稱加密算法,加密和解密過程的密鑰是相同的。
對稱加密算法優點是加解密效率(速度快,空間占用小)和加密強度都很高。 對稱加密算法缺點是參與方需要提前持有密鑰,一旦有人泄露則系統安全性被破壞;在不安全通道中提前分發密鑰是個問題,需要借助額外的Diffie–Hellman協商協議或非對稱加密算法來實現。
對稱密碼從實現原理上可以分為兩種:分組密碼和序列密碼。前者將明文切分為定長數據塊作為基本加密單位,應用最為廣泛。後者則每次只對一個字節或字符進行加密處理,且密碼不斷變化,只用在一些特定領域(如數字媒介的加密)。
分組對稱加密代表算法包括DES、3DES、AES、IDEA等。
DES(Data Encryption Standard):經典的分組加密算法,最早是1977年美國聯邦信息處理標準(FIPS)采用FIPS-46-3將64位明文加密為 64 位的密文。其密鑰長度為64位(包括 8位校驗碼),現在已經很容易被暴力破解。
3DES:三重DES操作,加密-->解密-->加密,處理過程和加密強度優於DES,但現在也被認為不夠安全。
AES(Advanced Encryption Standard):由美國國家標準研究所(NIST)采用,取代DES成為對稱加密實現的標準,1997~2000年NIST 從15個候選算法中評選Rijndael算法(比利時密碼學家Joan Daemon和Vincent Rijmen發明)作為AES,標準為FIPS-197。AES也是分組算法,分組長度為128、192、256位三種。AES的優勢在於處理速度快,整個過程可以數學化描述,目前尚未有有效的破解手段。
IDEA(International Data Encryption Algorithm):1991年由密碼學家James Massey與來學嘉共同提出。設計類似於3DES,密鑰長度增加到128位,具有更好的加密強度。
序列加密,又稱流加密。1949年,Claude Elwood Shannon(信息論創始人)首次證明,要實現絕對安全的完善保密性(Perfect Secrecy),可以通過“一次性密碼本”的對稱加密處理。即通信雙方每次使用跟明文等長的隨機密鑰串對明文進行加密處理。序列密碼采用了類似的思想,每次通過偽隨機數生成器來生成偽隨機密鑰串。代表算法包括RC4 等。
對稱加密算法適用於大量數據的加解密過程;不能用於簽名場景;並且需要提前安全地分發密鑰。
分組加密每次只能處理固定長度的明文,因此對於過長的內容需要采用一定模式進行分割,《實用密碼學》一書中推薦使用密文分組鏈(Cipher Block Chain,CBC)、計數器(Counter,CTR)等模式。
3、非對稱加密算法
非對稱加密是現代密碼學的偉大發明,有效解決了對稱加密需要安全分發密鑰的問題。
非對稱加密算法的加密密鑰和解密密鑰是不同的,分別被稱為公鑰(Public Key)和私鑰(Private Key)。私鑰一般通過隨機數算法生成,公鑰可以根據私鑰生成。公鑰一般是公開的,他人可獲取;私鑰則是個人持有並且要嚴密保護,不能被他人獲取。
非對稱加密算法優點是公私鑰分開,無需安全通道來分發密鑰。缺點是處理速度(特別是生成密鑰和解密過程)往往比較慢,一般比對稱加解密算法慢2~3個數量級;同時加密強度也不如對稱加密。
非對稱加密算法的安全性往往基於數學問題,包括大數質因子分解、離散對數、橢圓曲線等經典數學難題。
非對稱加密算法代表算法包括:RSA、ElGamal、橢圓曲線(Elliptic Curve Crytosystems,ECC)、SM2等系列算法。
RSA:經典的公鑰算法,1978 年由Ron Rivest、Adi Shamir、Leonard Adleman 共同提出,三人於2002年因此獲得圖靈獎。RSA算法利用了對大數進行質因子分解困難的特性,但目前還沒有數學證明兩者難度等價,或許存在未知算法可以繞過大數分解而進行解密。
ElGamal:由 Taher ElGamal 設計,利用了模運算下求離散對數困難的特性,比RSA產生密鑰更快,被應用在PGP等安全工具中。
橢圓曲線算法(Elliptic Curve Cryptography,ECC):現代備受關註的算法系列,基於對橢圓曲線上特定點進行特殊乘法逆運算難以計算的特性。最早在1985年由Neal Koblitz和Victor Miller分別獨立提出。ECC系列算法一般被認為具備較高的安全性,但加解密過程比較費時。
SM2(ShangMi 2):中國國家商用密碼系列算法標準,由中國密碼管理局於2010年12月17日發布,同樣基於橢圓曲線算法,一般認為其安全強度優於RSA系列算法。
非對稱加密算法適用於簽名場景或密鑰協商過程,但不適於大量數據的加解密。
RSA類算法被認為已經很難抵禦現代計算設備的破解,一般推薦商用場景下密鑰至少為2048位。如果采用安全強度更高的橢圓曲線算法,256 位密鑰即可滿足絕大部分安全需求。
4、選擇明文***
非對稱加密中公鑰是公開的,因此任何人都可以利用公鑰加密給定明文,獲取對應的密文,達到破解的目的,帶來選擇明文***的風險。
為了規避這種風險,現代的非對稱加密算法(如RSA、ECC)都引入了一定的保護機制:對同樣的明文使用同樣密鑰進行多次加密,得到的結果完全不同,避免了選擇明文***的破壞。
在實現上可以有多種思路。一種是對明文先進行變形添加隨機的字符串或標記,再對添加後結果進行處理。另外一種是先用隨機生成的臨時密鑰對明文進行對稱加密,然後再將對稱密鑰進行加密,即利用多層加密機制。
5、混合加密機制
混合加密機制同時結合了對稱加密和非對稱加密的優點。
混合加密機制的主要過程為:先用非對稱加密(計算復雜度較高)協商出一個臨時的對稱加密密鑰(或稱會話密鑰),然後雙方再通過對稱加密算法(計算復雜度較低)對所傳遞的大量數據進行快速的加密處理。
典型的應用案例是網站中使用越來越普遍的通信協議——安全超文本傳輸協議(Hyper Text Transfer Protocol Secure,HTTPS)。
與以明文方式傳輸數據的HTTP協議不同,HTTPS 在傳統的HTTP層和TCP層之間引入Transport Layer Security/Secure Socket Layer(TLS/SSL)加密層來實現安全傳輸。
SSL協議是HTTPS初期采用的標準協議,最早由Netscape 於1994年設計實現,其兩個主要版本(包括 v2.0和v3.0)曾得到大量應用。SSL 存在安全缺陷易受***(如 POODLE 和DROWN***),無法滿足現代安全需求,已於2011和2015年被 IETF宣布廢棄。基於SSL協議(v3.1),IETF提出了改善的安全標準協議TLS,成為目前廣泛采用的方案。2008年,TLS1.2版本發布,修正了之前版本的不少漏洞,極大增強了安全性,推薦商用場景使用。除了Web服務外,TLS 協議也被廣泛應用到FTP、Email、實時消息、音視頻通話等場
景中。
四、消息認證碼與數字簽名
1、消息認證碼
消息認證碼(Hash-based Message Authentication Code,HMAC),利用對稱加密,對消息完整性(Integrity)進行保護。
基本過程為對某個消息,利用提前共享的對稱密鑰和Hash算法進行處理,得到HMAC值。HMAC 值持有方可以向對方證明自己擁有某個對稱密鑰,並且確保所傳輸消息內容未被篡改。
典型的HMAC生成算法包括K,H,M三個參數。K為提前共享的對稱密鑰,H為提前商定的Hash算法(如SHA-256),M為要傳輸的消息內容。三個參數缺失任何一個,都無法得到正確的HMAC 值。
消息認證碼可以用於簡單證明身份的場景。如Alice、Bob提前共享了K和H。Alice 需要知曉對方是否為Bob,可發送一段消息M給Bob。Bob 到M後計算其HMAC值並返回給Alice,Alice檢驗收到HMAC值的正確性可以驗證對方是否真是Bob。
消息認證碼的主要問題是需要提前共享密鑰,並且當密鑰可能被多方同時擁有(甚至泄露)的場景下,無法追蹤消息的真實來源。
2、數字簽名
數字簽名既可以證實某數字內容的完整性,又可以確認其來源(即不可抵賴,Non-Repudiation)。
一個典型的場景是Alice通過信道發給Bob一個文件(一份信息),Bob如何獲知所收到的文件即為Alice發出的原始版本?Alice可以先對文件內容進行摘要,然後用自己的私鑰對摘要進行加密(簽名),之後同時將文件和簽名都發給Bob。Bob收到文件和簽名後,用Alice的公鑰來解密簽名,得到數字摘要,與對文件進行摘要後的結果進行比對。如果一致,說明該文件確實是Alice發過來的(因為別人無法擁有Alice的私鑰),並且文件內容沒有被修改過(摘要結果一致)。
理論上所有的非對稱加密算法都可以用來實現數字簽名,實踐中常用算法包括1991年8 月NIST提出的DSA(Digital Signature Algorithm,基於ElGamal 算法)和安全強度更高的ECSDA(Elliptic Curve Digital Signature Algorithm,基於橢圓曲線算法)等。
除普通的數字簽名應用場景外,針對一些特定的安全需求,產生了一些特殊數字簽名技術,包括盲簽名、多重簽名、群簽名、環簽名等。
3、盲簽名
盲簽名(Blind Signature),1982 年由David Chaum在論文《Blind Signatures for Untraceable Payment》中提出。簽名者需要在無法看到原始內容的前提下對信息進行簽名。
盲簽名可以實現對所簽名內容的保護,防止簽名者看到原始內容;另一方面,盲簽名還可以實現防止追蹤(Unlinkability),簽名者無法將簽名內容和簽名結果進行對應。典型的實現包括RSA盲簽名算法等。
4、多重簽名
多重簽名(Multiple Signature),即 n個簽名者中,收集到至少m(n>=m>=1)的簽名,即認為合法。其中,n是提供的公鑰個數,m是需要匹配公鑰的最少的簽名個數。
多重簽名可以有效地被應用在多人投票共同決策的場景中。例如雙方進行協商,第三方作為審核方。三方中任何兩方達成一致即可完成協商。
比特幣交易中就支持多重簽名,可以實現多個人共同管理某個賬戶的比特幣交易。
5、群簽名
群簽名(Group Signature),即某個群組內一個成員可以代表群組進行匿名簽名。簽名可以驗證來自於該群組,卻無法準確追蹤到簽名的是哪個成員。
群簽名需要存在一個群管理員來添加新的群成員,因此存在群管理員可能追蹤到簽名成員身份的風險。
群簽名最早在1991 年由David Chaum和 Eugene van Heyst提出。
6、環簽名
環簽名(Ring Signature),由Rivest,Shamir和Tauman 三位密碼學家在2001年首次提出。環簽名屬於一種簡化的群簽名。
簽名者首先選定一個臨時的簽名者集合,集合中包括簽名者自身。然後簽名者利用自己的私鑰和簽名集合中其他人的公鑰就可以獨立的產生簽名,而無需他人的幫助。簽名者集合中的其他成員可能並不知道自己被包含在最終的簽名中。
環簽名在保護匿名性方面也具有很多用途。
五、數字證書
1、數字證書簡介
對於非對稱加密算法和數字簽名,很重要的步驟就是公鑰的分發。理論上任何人都可以獲取到公開的公鑰。然而公鑰文件有沒可能是偽造的,傳輸過程中可能被篡改,一旦公鑰自身出了問題,則整個建立在其上的的安全性將不復成立。
數字證書機制正是為了解決公鑰分發問題,可以確保所記錄信息的合法性。比如證明某個公鑰是某個實體(個人或組織)擁有,並且確保任何篡改都能被檢測出來,從而實現對用戶公鑰的安全分發。
根據所保護公鑰的用途,數字證書可以分為加密數字證書(Encryption Certificate)和簽名驗證數字證書(Signature Certificate)。前者往往用於保護用於加密用途的公鑰;後者則保護用於簽名用途的公鑰。兩種類型的公鑰也可以同時放在同一證書中。
一般情況下,證書需要由證書認證機構(Certification Authority,CA)來進行簽發和背書。權威的商業證書認證機構包括DigiCert、GlobalSign、VeriSign等。用戶也可以自行搭建本地CA系統,在私有網絡中進行使用。
2、X.509證書規範
通常,一個數字證書內容可能包括證書域(證書的版本、序列號、簽名算法類型、簽發者信息、有效期、被簽發主體、簽發的公開密鑰)、CA對證書的簽名算法和簽名值等。目前使用最廣泛的標準為ITU和ISO聯合制定的X.509的v3版本規範(RFC5280),其中定義了如下證書信息域:
版本號(Version Number):規範的版本號,目前為版本 3,值為0x2
序列號(Serial Number):由CA維護的為所頒發的每個證書分配的唯一的序列號,用來追蹤和撤銷證書。只要擁有簽發者信息和序列號,就可以唯一標識一個證書。最大不能超過20個字節
簽名算法(Signature Algorithm):數字簽名所采用的算法,如sha256WithRSAEncryption 或 ecdsa-with-SHA256
頒發者(Issuer):頒發證書單位的信息,如“C=CN,ST=Beijing,
L=Beijing,O=org.example.com,CN=ca.org.example.com”;
有效期(Validity):證書的有效期限,包括起止時間(如 Not Before 2018-08-08-00-00UTC,Not After 2028-08-08-00-00UTC);
被簽發主體(Subject):證書擁有者的標識信息(Distinguished Name),如“C=CN, ST=Beijing, L=Beijing, CN=personA.org.example.com”;
主體的公鑰信息(Subject Public Key Info):所保護的公鑰相關的信息;
A、公鑰算法(Public Key Algorithm):公鑰采用的算法;
B、主體公鑰(Subject Public Key):公鑰的內容;
頒發者唯一號(Issuer Unique Identifier,可選):代表頒發者的唯一信息,僅2、3版本支持,可選;
主體唯一號(Subject Unique Identifier,可選):代表擁有證書實體的唯一信息,僅 2、3版本支持,可選。
擴展(Extensions,可選):可選的一些擴展。可能包括:
Subject Key Identifier:實體的密鑰標識符,區分實體的多對密鑰;
Basic Constraints:一般指明該證書是否屬於某個CA;
Authority Key Identifier:頒發這個證書的頒發者的公鑰標識符;
Authority Information Access:頒發相關的服務地址,如頒發者證書獲取地址和吊銷證書列表信息查詢地址;
CRL Distribution Points:證書註銷列表的發布地址;
Key Usage: 表明證書的用途或功能信息,如Digital Signature、Key CertSign;
Subject Alternative Name:證書身份實體的別名,如該證書可以同樣表.org.example.com,org.example.com,.example.com,example.com身份等。
此外,證書的頒發者還需要對證書內容利用自己的私鑰進行簽名,以防止他人篡改證書內容。
3、證書格式
X.509規範中一般推薦使用PEM(Privacy Enhanced Mail)格式來存儲證書相關的文件。證書文件的文件名後綴一般為.crt或.cer,對應私鑰文件的文件名後綴一般為.key,證書請求文件的文件名後綴為.csr 。有時候也統一用.pem作為文件名後綴。
PEM格式采用文本方式進行存儲,一般包括首尾標記和內容塊,內容塊采用base64編碼。
例如,一個示例證書文件的PEM 格式如下所示。
-----BEGIN CERTIFICATE-----
MIICMzCCAdmgAwIBAgIQIhMiRzqkCljq3ZXnsl6EijAKBggqhkjOPQQDAjBmMQsw
CQYDVQQGEwJVUzETMBEGA1UECBMKQ2FsaWZvcm5pYTEWMBQGA1UEBxMNU2FuIEZy
YW5jaXNjbzEUMBIGA1UEChMLZXhhbXBsZS5jb20xFDASBgNVBAMTC2V4YW1wbGUu
Y29tMB4XDTE3MDQyNTAzMzAzN1oXDTI3MDQyMzAzMzAzN1owZjELMAkGA1UEBhMC
VVMxEzARBgNVBAgTCkNhbGlmb3JuaWExFjAUBgNVBAcTDVNhbiBGcmFuY2lzY28x
FDASBgNVBAoTC2V4YW1wbGUuY29tMRQwEgYDVQQDEwtleGFtcGxlLmNvbTBZMBMG
ByqGSM49AgEGCCqGSM49AwEHA0IABCkIHZ3mJCEPbIbUdh/Kz3zWW1C9wxnZOwfy
yrhr6aHwWREW3ZpMWKUcbsYup5kbouBc2dvMFUgoPBoaFYJ9D0SjaTBnMA4GA1Ud
DwEB/wQEAwIBpjAZBgNVHSUEEjAQBgRVHSUABggrBgEFBQcDATAPBgNVHRMBAf8E
BTADAQH/MCkGA1UdDgQiBCBIA/DmemwTGibbGe8uWjt5hnlE63SUsXuNKO9iGEhV
qDAKBggqhkjOPQQDAgNIADBFAiEAyoMO2BAQ3c9gBJOk1oSyXP70XRk4dTwXMF7q
R72ijLECIFKLANpgWFoMoo3W91uzJeUmnbJJt8Jlr00ByjurfAvv
-----END CERTIFICATE-----可以通過openssl 工具來查看其內容,使用如下:openssl x509 -in example.com-cert.pem -noout -text
此外,還有DER(Distinguished Encoding Rules)格式,是采用二進制對證書進行保存,可以與PEM格式互相轉換。
3、證書信任鏈
證書中記錄了大量信息,其中最重要的包括簽發的公開密鑰和CA數字簽名兩個信息。因此,只要使用CA的公鑰再次對證書進行簽名比對,就能證明所記錄的公鑰是否合法。
CA的公鑰是否合法,一方面可以通過更上層的CA頒發的證書來進行認證;另一方面某些根CA(Root CA)可以通過預先分發證書來實現信任基礎。例如,主流操作系統和瀏覽器裏面,通常會提前預置一些權威CA的證書(通過自身的私鑰簽名,系統承認是合法的證書)。所有基於預置權威CA認證過的中間層CA(Intermediate CA)和後繼 CA 都會被驗證合法。從預先信任的根證書,經過中間層證書,到最底下的實體證書,構成一條完整的證書信任鏈。
某些時候用戶在使用瀏覽器訪問某些網站時,可能會被提示是否信任對方的證書。說明網站證書無法被當前系統中的證書信任鏈進行驗證,需要進行額外檢查。另外,當信任鏈上任一證書不可靠時,則依賴它的所有後繼證書都將失去保障。
因此,證書作為公鑰信任的基礎,對其生命周期進行安全管理十分關鍵。
六、PKI體系
1、PKI簡介
按照X.509規範,公鑰可以通過證書機制來進行保護,但證書的生成、分發、撤銷等步驟並未涉及。要實現安全地管理、分發證書需要遵循PKI(Public Key Infrastructure)體系。PKI體系提供了一套完整的證書管理的框架,包括生成、頒發、撤銷過程等,解決了證書生命周期相關的認證和管理問題。
PKI是建立在公私鑰基礎上實現安全可靠傳遞消息和身份確認的一個通用框架,並不代表某個特定的密碼學技術和流程。實現了PKI規範的平臺可以安全可靠地管理網絡中用戶的密鑰和證書。目前包括多個具體實現和規範,知名的有RSA公司的PKCS(Public Key Cryptography Standards)標準和OpenSSL等開源工具。
通常,PKI至少包括如下核心組件:
CA(Certification Authority):負責證書的頒發和吊銷(Revoke),接收來自 RA 的請求,是最核心的部分,主要完成對證書信息的維護;
RA(Registration Authority):對用戶身份進行驗證,校驗數據合法性,負責登記,審核過就發給CA;
證書數據庫:存放證書,多采用X.500系列標準格式。可以配合LDAP 目錄服務管理用戶信息。
常見的操作流程為,用戶通過RA登記申請證書,提供身份和認證信息等;CA 審核後完成證書的制造,頒發給用戶。用戶如果需要撤銷證書則需要再次向CA 發出申請。
2、證書簽發
CA 對用戶簽發證書實際上是對某個用戶公鑰,使用CA的私鑰對其進行簽名。任何人都可以用CA 的公鑰對該證書進行合法性驗證。驗證成功則認可該證書中所提供的用戶公鑰內容,實現用戶公鑰的安全分發。
用戶證書的簽發可以有兩種方式。可以由用戶自己生成公鑰和私鑰,然後CA來對公鑰內容進行簽名(只有用戶持有私鑰);也可以由 CA 直接來生成證書(內含公鑰)和對應的私鑰發給用戶(用戶和CA均持有私鑰)。前者情況下,用戶一般會首先自行生成一個私鑰和證書申請文件(Certificate Signing Request,即csr 文件),CSR文件中包括了用戶對應的公鑰和一些基本信息,如通用名
(common name,即cn)、組織信息、地理位置等。CA只需要對證書請求文件進行簽名,生成證書文件,頒發給用戶即可。整個過程中,用戶可以保持私鑰信息的私密性,不會被其他方獲知(包括CA方)。
生成證書申請文件的過程並不復雜,用戶可以很容易地使用開源軟件openssl來生成csr 文件和對應的私鑰文件。
安裝openssl後可以執行如下命令來生成私鑰和對應的證書請求文件:openssl req -new -keyout private.key -out for_request.csr
生成過程中需要輸入地理位置、組織、通用名等信息。生成的私鑰和csr文件默認以PEM格式存儲,內容為base64編碼。
openssl工具提供了查看PEM 格式文件明文的功能,如使用如下命令可以查看生成的csr文件的明文:openssl req -in for_request.csr -noout -text
用戶自行生成私鑰情況下,私鑰文件一旦丟失,CA 方由於不持有私鑰信息,無法進行恢復,意味著通過該證書中公鑰加密的內容將無法被解密。
3、證書吊銷
證書超出有效期後會作廢,用戶也可以主動向CA申請吊銷某證書文件。由於CA無法強制收回已經頒發出去的數字證書,因此為了實現證書的作廢,往往還需要維護一個吊銷證書列表(Certificate Revocation List,CRL),用於記錄已經吊銷的證書序號。因此,通常情況下,當對某個證書進行驗證時,需要首先檢查該證書是否已經記錄在列表中。如果存在,則該證書無法通過驗證。如果不在,則繼續進行後續的證書驗證過程。
為了方便同步吊銷列表信息,IETF提出了在線證書狀態協議(Online Certificate Status Protocol,OCSP),支持該協議的服務可以實時在線查詢吊銷的證書列表信息。
七、Merkel樹
1、Merkel樹簡介
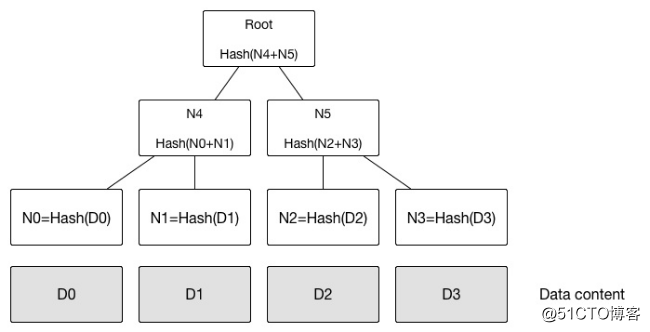
默克爾樹(又叫哈希樹)是一種典型的二叉樹結構,由一個根節點、一組中間節點和一組葉節點組成。默克爾樹最早由Merkle Ralf在1980 年提出,曾廣泛用於文件系統和P2P系統中。其主要特點如下:
A、最下面的葉節點包含存儲數據或其哈希值。
B、非葉子節點(包括中間節點和根節點)都是其兩個孩子節點內容的哈希值。
默克爾樹可以推廣到多叉樹的情形,此時非葉子節點的內容為其所有的孩子節點的內容的哈希值。
默克爾樹逐層記錄哈希值的特點,讓其具有了一些獨特的性質。例如,底層數據的任何變動,都會傳遞到其父節點,一層層沿著路徑一直到樹根。樹根的值實際上代表了對底層所有數據的“數字摘要”。
2、Merkel樹的應用場景
(1)快速比較大量數據
對每組數據排序後構建默克爾樹結構。當兩個默克爾樹根相同時,則所代表的兩組數據必然相同。否則,必然不同。
由於Hash計算的過程可以十分快速,預處理可以在短時間內完成。利用默克爾樹結構能帶來巨大的比較性能優勢。
(2)快速定位修改
如果D1中數據被修改,會影響到N1,N4 和Root。
一旦發現某個節點如Root的數值發生變化,沿著 Root-->N4-->N1,最多通過O(lgn)時間即可快速定位到實際發生改變的數據塊D1。
(3)零知識證明
如何向他人證明擁有的某組數據(D0......D3)中包括給定某個內容D0而不
暴露其它任何內容。
對於本文所示默克爾樹,公布N1,N5,Root。驗證者計算Root值,驗證是否跟提供值一致,即可很容易檢測D0存在。整個過程中驗證者無法獲知其它任何信息。
八、布隆過濾器
1、布隆過濾器簡介
布隆過濾器(Bloom Filter),1970年由 Burton Howard Bloom在論文《Space/Time Trade-offs in Hash Coding with Allowable Errors》提出。布隆過濾器是一種基於Hash的高效查找結構,能夠快速(常數時間內)回答“某個元素是否在一個集合內”的問題。
布隆過濾器結構因為其高效性,被大量應用到網絡和安全領域,例如信息檢索(BigTable和HBase)、垃圾郵件規則、註冊管理等。
2、基於Hash的快速查找
Hash可以將任意內容映射到一個固定長度的字符串,而且不同內容映射到相同串的概率很低,構成了一個很好的“內容->索引”的生成關系。
如果給定一個內容和存儲數組,通過構造Hash函數,讓映射後的Hash值總不超過數組的大小,則可以實現快速的基於內容的查找。例如,內容“hello world”的 Hash值如果是“100”,則存放到數組的第100 個單元上。如果需要快速查找任意內容,如“hello world”字符串是否在存儲系統中,只需要將其在常數時間內計算Hash值,並用Hash值查看系統中對應元素即可。
然而,當映射後的值限制在一定範圍(如總數組的大小)內時,會發現Hash沖突的概率會變高,而且範圍越小,沖突概率越大。很多時候,存儲系統的大小又不能無限擴展,造成算法效率的下降。為了提高空間利用率,基於Hash 算法的思想設計出了布隆過濾器結構。
3、布隆過濾器實現原理
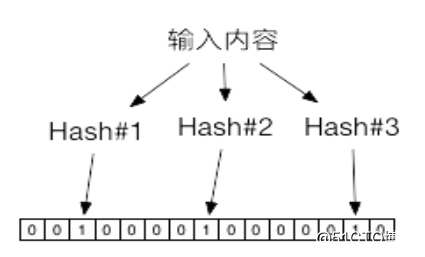
布隆過濾器采用多個Hash函數來提高空間利用率。
對同一個給定輸入,多個Hash函數計算出多個地址,分別在位串的這些地址上標記為1。進行查找時,進行同樣的計算過程,並查看對應元素,如果都為1,則說明較大概率是存在該輸入。
布隆過濾器相對單個Hash算法查找,大大提高了空間利用率,可以使用較少的空間來表示較大集合的存在關系。
無論是Hash,還是布隆過濾器,基本思想都是基於內容的編址。
Hash函數存在沖突,布隆過濾器也存在沖突,兩種方法都存在著誤報(False Positive)的情況,但絕對不會漏報(False Negative)。布隆過濾器在應用中誤報率通常很低,例如,在使用7個不同Hash函數的情況下,記錄100 萬個數據,采用2MB大小的位串,整體的誤判率將低於1%。而傳統的Hash查找算法的誤報率將接近10%。
九、同態加密
1、同態加密簡介
同態加密(Homomorphic Encryption)是一種特殊的加密方法,允許對密文進行處理得到仍然是加密的結果。即對密文直接進行處理,跟對明文進行處理後再對處理結果加密,得到的結果相同。從抽象代數的角度講,保持了同態性。
同態性來自代數領域,一般包括四種類型:加法同態、乘法同態、減法同態和除法同態。同時滿足加法同態和乘法同態,則意味著是代數同態,即全同態(Full Homomorphic)。同時滿足四種同態性,則被稱為算數同態。
對於計算機操作來講,實現了全同態意味著對於所有處理都可以實現同態性。只能實現部分特定操作的同態性,被稱為特定同態(Somewhat Homomorphic)。
2、同態加密的問題與挑戰
同態加密的問題最早由Ron Rivest、Leonard Adleman和Michael L.Dertouzos 在1978年提出,同年提出RSA加密算法。但第一個“全同態”的算法直到2009年才被Craig Gentry在論文《Fully Homomorphic Encryption Using Ideal Lattices》中提出並進行數學證明。
僅滿足加法同態的算法包括Paillier和Benaloh算法;僅滿足乘法同態的算法包括RSA和ElGamal 算法。
同態加密在雲計算和大數據的時代意義十分重大。目前,雖然雲計算帶來了包括低成本、高性能和便捷性等優勢,但從安全角度講,用戶還不敢將敏感信息直接放到第三方雲上進行處理。如果有比較實用的同態加密技術,則大家就可以放心的使用各種雲服務,同時各種數據分析過程也不會泄露用戶隱私。加密後的數據在第三方服務處理後得到加密後的結果,結果只有用戶自身可以進行解密,整個過程第三方平臺無法獲知任何有效的數據信息。
另一方面,對於區塊鏈技術,同態加密也是很好的互補。使用同態加密技術,運行在區塊鏈上的智能合約可以處理密文,而無法獲知真實數據,極大的提高了隱私安全性。
目前全同態的加密方案主要包括如下三種類型:
A、基於理想格(ideal lattice)的方案
Gentry和Halevi在2011年提出的基於理想格的方案可以實現 72 bit 的安全強度,對應的公鑰大小約為2.3GB,同時刷新密文的處理時間需要幾十分鐘。
B、基於整數上近似GCD問題的方案
Dijk等人在2010年提出的方案(及後續方案)采用了更簡化的概念模型,可以降低公鑰大小至幾十MB量級。
C、基於帶擾動學習(Learning With Errors,LWE)問題的方案
Brakerski和Vaikuntanathan等在2011年左右提出了相關方案;Lopez-Alt A等在2012年設計出多密鑰全同態加密方案,接近實時多方安全計算的需求。
目前,已知的同態加密技術往往需要較高的計算時間或存儲成本,相比傳統加密算法的性能和強度還有差距,但同態加密技術領域關註度一直很高。
3、函數加密
與同態加密相關的一個問題是函數加密。同態加密保護的是數據本身,而函數加密顧名思義保護的是處理函數本身,即讓第三方看不到處理過程的前提下,對數據進行處理。
函數加密問題已被證明不存在對多個通用函數的任意多密鑰的方案,目前僅能做到對某個特定函數的一個密鑰的方案。
十、其它安全技術
1、零知識證明
知識證明(Zero Knowledge Proof)是證明者在不向驗證者提供任何額外信息的前提下,使驗證者相信某個論斷是正確的過程。
證明過程包括交互式和費交互式兩種。
例如,Alice向Bob 證明自己知道某個數字,在證明過程中Bob可以按照某個順序提出一系列問題(比如數字加上某些隨機數後的變換)由 Alice進行回答,並通過回答最終確信Alice較大概率確實知道某數字。證明過程中,Bob除了知道Alice確實知道該數字這個論斷外,自己無法獲知或推理出任何額外信息(包括該數字本身),也無法用 Alice的證明(例如證明過程的錄像)去向別人證明。註意這個過程中Alice如果提前猜測出 Bob問題的順序,則存在作假的可能性。
零知識證明的研究始於1985年Shafi Goldwasser等人的論文《The Knowledge Complexity of Interactive Proof-Systems》,目前一般認為至少要滿足三個條件:
A、完整性(Completeness):真實的證明可以讓驗證者成功驗證。
B、可靠性(Soundness):虛假的證明無法保證通過驗證,但理論上存在小概率例外。
C、零知識(Zero-Knowledge):如果得到證明,無法從證明過程中獲知除了所證明信息之外的任何信息。
2、可驗證隨機函數
可驗證隨機函數(Verifiable Random Function,VRF)最早由Silvio Micali(MIT)、Michael Rabiny(哈佛大學)、Salil Vadha(MIT)於1999年在論文《Verifiable Random Functions》中提出。
VRF討論的是一類特殊的偽隨機函數,其結果可以在某些場景下進行驗證。
例如,Alice擁有公鑰Pk和對應私鑰 Sk。Alice宣稱某可驗證隨機函數 F和一個輸入x,並計算y = F(Sk, x)。Bob可以使用Alice公鑰Pk,對同樣的x和F進行驗證,證明其結果確實為y。因為F的隨機性,任何人都無法預測y的值。
VRF提供了一種讓大家都認可並且可以驗證的隨機序列,可以用於分布式系統中進行投票的場景。目前已經有利用VRF的共識算法VBFT。
3、量子密碼學
量子密碼學(Quantum Cryptography)隨著量子計算和量子通信的研究而被受到越來越多的關註,被認為會對已有的密碼學安全機制產生較大的影響。
量子計算的概念最早是物理學家費曼於1981年提出,基本原理是利用量子比特可以同時處於多個相幹疊加態,理論上可以同時用少量量子比特來表達大量的信息,並同時進行處理,大大提高計算速度。量子計算目前在某些特定領域已經展現出超越經典計算的潛力。如基於量子計算的Shor算法(1994 年提出),理論上可以實現遠超經典計算速度的大數因子分解。
2016年3月,人類第一次以可擴展的方式,用 Shor算法完成對數字15的質因數分解。目前廣泛應用的非對稱加密算法,包括基於大整數分解的RSA、基於橢圓曲線隨機數的ECC等將來都將很容易被破解。當然,現代密碼學體系並不會因為量子計算的出現而崩潰。一方面,量子計算設備離實際可用的通用計算機還有較大距離,密碼學家可以探索更安全的密碼算法。另一方面,很多安全機制尚未發現能加速破解的量子算法,包括數字簽名(基於Hash)、格(Lattice)密碼、基於編碼的密碼等。
量子通信則可以提供對密鑰進行安全協商的機制,有望實現無條件安全的“一次性密碼”。量子通信基於量子糾纏效應,兩個發生糾纏的量子可以進行遠距離的實時狀態同步。一旦信道被竊聽,則通信雙方會獲知該情況,丟棄此次傳輸的泄露信息,十分適合進行大量的密鑰分發,如1984年提出的BB84 協議,結合量子通道和公開信道,可以實現安全的密鑰分發。
一次性密碼最早由香農提出,實現理論上絕對安全的對稱加密。其特點為密鑰真隨機且只使用一次;密鑰長度跟明文一致,加密過程為兩者進行二進制異或操作。
4、社交工程學
密碼學與安全問題,一直是學術界和工業界都十分關心的重要話題,相關的技術也一直在不斷發展和完善。然而,即便存在理論上完美的技術,也不存在完美的系統。看起來設計十分完善的系統最後被攻破,並非是因為設計上出現了深層次的漏洞。而問題往往出在事後看來十分淺顯的一些方面。例如,系統管理員將登陸密碼貼到電腦前;財務人員在電話裏泄露用戶的個人敏感信息;公司職員隨意運行來自不明郵件的附件;不明人員借推銷或調查問卷的名義進入辦公場所竊取信息等
區塊鏈快速入門(六)——區塊鏈密碼學與安全相關技術
