差分數組

定義

百度百科中的差分定義
//其實這完全和要講的沒關系 qwq

進去看了之後是不是覺得看不懂？

那我簡單概括一下qwq

差分數組de定義：記錄當前位置的數與上一位置的數的差值.

栗子

容易發現的是,\(\sum_{j=1}^{i} b_j\)即代表\(a_i\) 的值. \((\sum\) 即代表累加.)

思想

看到前面的\(\sum\) 你一定會發現這是前綴和!

那你認為這是前綴和? 的確是qwq.

實際上這並不是真正意義上的前綴和.

前綴和的思想是 根據元素與元素之間的並集關系(和的關系),求出某些元素的和的值.對應的為$\sum_{j=1}^{i} a_j $

而差分的思想與此不同.

差分的思想是 根據元素與元素之間的邏輯關系(大小關系),求出某一位置元素的值.對應的為\(\sum_{j=1}^{i} b_j\)

What?不懂?看下面

繼續撿起剛剛的栗子.

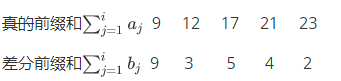
有沒有發現不同之處 ( ? ?ω?? )?

差分數組有什麽用?

先看一道題,

有n個數。

m次操作,每一次操作,給定l,r,del.將l~r區間的所有數增加del；

最後有q個詢問,給你 l,r ,每一次詢問求出l~r的區間和。

PS： 先進行m個修改操作,後進行查詢操作.

如果你是一個巨佬,你會"woc,線段樹裸題!" "woc,樹狀數組裸題!"

然而,今天我要BB的不是這些東西.

是差分數組的運用!

有沒有想法? 沒有的話那就我來有也是我來

考慮我們差分數組記錄的是什麽,它記錄的是當前位置的數與上一個數的差值.

如果我們在差分數組的 \(b_x\)減去\(del\) 在\(b_{y+1}\)位置處加上\(del\),就能達到整個區間修改的操作.

什麽?不相信? 那我們來個栗子(要糖炒的

還是剛開始的栗子.

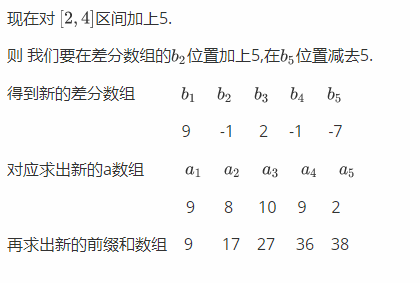
這樣是不是達到了區間修改操作,是不是! "是!,tql!!"

這樣我們就能做到\(O(1)\)修改啦!

我們再定義兩個數組(先不要忘記我們的差分數組為\(b_i\)

\(s_i\)代表\(\sum_{j=1}^{i} b_j\) (其實就是代表\(a[i]\)

qwq

\(sum_i\)代表\(\sum_{j=1}^{i} s_j\) 即代表前綴和. qwq

容易發現的是 \(sum_r -sum_{l-1}=\sum_{i=l}^{r} s_i\)

什麽不理解為什麽是\(l-1\)？

那我們把式子展開看 qwq

\(sum_r=s_1+s_2+\dots+s_{l-1}+s_{l}+s_{l+1}+\dots+s_r\)

\(sum_{l-1}=s_1+s_2+\dots+s_{l-2}+s_{l-1}\)

兩個式子相減的話,我們得到的就是 \(s_l+\dots+s_r\) 即\(\sum_{i=l}^r s_i\)啦!

而我們如果減去\(sum_l\)的話,就會多減去一個s_l,得到的值就不是\(\sum_{i=l}^r s_i\) 了!

emmmm 差點跑去講前綴和

所以說我們可以在修改操作完成之後,\(O(n)\)的計算我們的\(sum\)數組,然後在詢問的時候\(O(1)\)的輸出了.

具體這個題的代碼是這樣的↓

#include<bits/stdc++.h>
using namespace std;
int n,m,q,last,sum[10086],b[10086],s[10086];
int main()
{
    cin>>n;//n個數 
    for(int i=1,x;i<=n;i++)
    {
        cin>>x;//這裏實際上不需要a數組,視題而異 
        b[i]=x-last;//得到差分數組 
        last=x;//別忘了變化last變量 
    }
    cin>>m;//m次操作
    for(int i=1,l,r,del;i<=m;i++)
    {
         cin>>l>>r>>del;//在[l,r] 加上del
         b[l]+=del,b[r+1]-=del; 
    }
    for(int i=1;i<=n;i++)
    {
        s[i]=s[i-1]+b[i];//這裏是處理我們的s數組 
        sum[i]=sum[i-1]+s[i];//處理我們的sum數組. 
    }
    cin>>q;//q個詢問 
    for(int i=1,l,r;i<=q;i++)
    {
        cin>>l>>r; //詢問[l,r]的區間和.
        cout<<sum[r]-sum[l-1]<<endl; //輸出即可. 
    }
}

剛剛涉及到的用途有

1. 快速處理區間加減操作：\(O(1)\)
2. 詢問區間和:\(O(n)\)處理\(O(1)\)查詢.

你以為差分只有這麽多用處嗎?

利用差分數組還能算出前綴和,看式子變形!

所以說,上面的代碼完全可以改一下,相信大家寫出來應該會很容易. (其實是我懶 qwq

差分還有其他用途這裏並沒有涉及到,所以還需要大家自己去發現去學習 ┓( ′?｀ )┏

稱不上是拓展的拓展

xor差分

其實剛開始聽到這個名字還是很迷的emmm

感謝咕咕日報的管理大大告訴我有這個東西才能學來分享給大家

這裏給出如何求這種情況下的差分數組.

n++;//原長度要+1,因為我們差分數組用到了右端點右邊一位.
for(int i=1;i<=n;i++)b[i]=a[i]^a[i-1];//與上一位異或。

思想

類比於普通差分的思想,我們在被修改區間的左端點\(b_l\)^= 1,右端點的右側\(b_{r+1}\)^=1.

但是這樣可行嗎?

再來一個栗子 (幹炒

我們將差分數組一路滾過去 發現\(\sum_{j=1}^{i}b_j\)依舊等於\(a_i\)

這證明xor是可以差分的!

然後我們嘗試翻轉a_2 到a_4這段區間.

根據差分數組的思想,我們將 \(b_2\)^=1 再將 \(b_5\)^=1

得到新的一組對應關系是這樣的 ↓ qwq

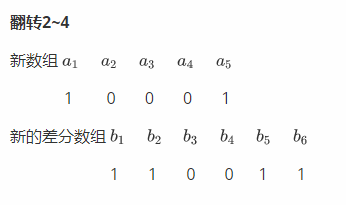
我們再把差分數組滾過去,發現依舊對應 ! 太神奇了!

事實證明這個是對的.(具體證明的話,我不會 qwq.

例題

來一個 差分+二分 結合運用的題目 -->p1083 借教室

看完題目了沒? 有沒有思路?

想一下,

在 一個訂單的起始天+要借的教室數量, 並在該訂單結束的那一天的下一天減去要借的教室數量

這樣我們再維護一下前綴和,這就樣就能知道這些天中,我們借了多少教室! 是不是很巧妙qwq

然後我們再二分訂單數量,嘗試滿足mid個訂單,(這個不會證明 QAQ)

因此我們ok函數這樣寫 ↓

IL bool ok(int now)//嘗試滿足now個訂單 
{
    clear(delt);
    for(RI i=1;i<=now;i++)
    {
        delt[s[i]]+=d[i];//s[i]為第i個訂單起始天
        delt[t[i]+1]-=d[i];//t[i]為第i個訂單結束天.
    }
    for(RI i=1;i<=n;i++)
    {
        sum[i]=sum[i-1]+delt[i];//前綴和.
        if(sum[i]>could[i])return false;
    }
    return true;
}

相信你隨隨便便也能切掉這個題了.

小結

差分數組的話,一般並沒有裸的考查,但是差分數組的思想啊,輔助啊,還是比較常用的qwq.

例如樹狀數組維護差分(到底是誰維護誰我也不是很清楚)qwq

(因為樹狀數組是維護的前綴和啊,所以可以一起用)

推薦一篇很好的文章(講解樹狀數組與差分的結合使用)--->這裏

Chanis寫的也很好啊qwq

如果非要說差分數組的適用範圍的話,

它適用於離線的區間修改問題,在線的話就去碼 線段Tree 或 Tree狀數組就好了 qwq

課下作業

差分的板子題loj　洛谷

題解戳這裏

p3943 星空 xor差分+最短路? (我也沒有做啊 qwq

p3948 數據結構 一道差分的簡單題 qwq.

這兩個題我只碼了第二題的代碼

第一題有時間再做 qwq

樹上差分

其實主要是為了講這個的qwq

2015,2016兩年Noip對於樹上差分都有考察 noip2015 運輸計劃 noip2016 天天愛跑步

這兩個題涉及的知識點有著 樹上差分+二分+LCA\(\dots\),這是一些進階的考查 其實是我不太會qwq

所以在這裏打算單純地介紹一下樹上差分並講解一些例題.qwq

前置知識

需要知道的樹的性質:

1. 樹上任意兩個點的路徑唯一.

2. 任何子節點的父親節點唯一.(可以認為根節點是沒有父親的)

如果你認為你知道了這些你就能秒切這些樹上差分的題,那你就太低估這個東西了!

樹上差分的兩種基本操作用到了LCA,不了解LCA的話可以去這裏面學一下

思想

類比於差分數組,樹上差分利用的思想也是前綴和思想.(在這裏應該是子樹和思想.

當我們記錄樹上節點被經過的次數,記錄某條邊被經過的次數的時候.

如果每次強制dfs去標記的話,時間復雜度將高到爆炸!

因此我們引入了樹上差分!

與樹上差分在一起的使用的是\(DFS\)，因為在回溯的時候,我們可以計算出子樹的大小.

(這個應該不用過多解釋

定義數組

\(cnt_i\)為節點i被經過的次數.

基本操作

1.點的差分

這個比較簡單,所以先講這個qwq

例如,我們從 \(s-->t\) ,求這條路徑上的點被經過的次數.

很明顯的,我們需要找到他們的LCA,(因為這個點是中轉點啊qwq.

我們需要讓\(cnt_s++\),讓\(cnt_t++\)，而讓他們的\(cnt_{lca}--\)，\(cnt_{faher(lca)}--\);

可能讀著會有些難理解,所以我準備了一個圖qwq

綠色的數字代表經過次數.

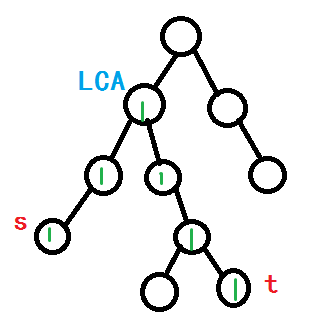
直接去標記的話,可能會T到不行,但是我們現在在講啥?樹上差分啊!

根據剛剛所講,我們的標記應該是這樣的↓

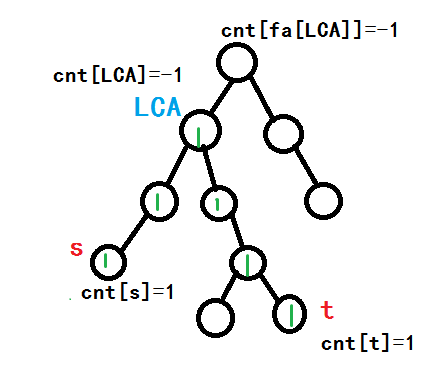
考慮：我們搜索到s,向上回溯.

下面以\(u\)表示當前節點,\(son_i\)代表i的兒子節點.(如果一些\(son\)不給出下標,即代表當前節點\(u\)的兒子

每個\(u\)統計它的子樹大小,順著路徑標起來.(即\(cnt_u+=cnt_{son}\))

我們會發現第一次從s回溯到它們的LCA時候,\(cnt_{LCA}+=cnt[son_{LCA}]\)

\(cnt_{LCA}=0\)! "不是LCA會被經過一次嘛,為什麽是0!"

別急,我們繼續搜另一邊.

繼續：我們搜索到t,向上回溯.

依舊統計每個u的子樹大小\(cnt_u+=cnt_{son}\)

再度回到\(LCA\) 依舊 是\(cnt_{LCA}+=cnt[son_{LCA}]\)

這個時候 \(cnt_{LCA}=1\) 這就達到了我們要的效果 (是不是特別優秀 ( ? ?ω?? )?

擔憂： 萬一我們再從\(LCA\)向上回溯的時候使得其父親節點的子樹和為1怎麽辦?

這樣我們不就使得其父親節點被經過了一次? 因此我們需要在\(cnt_{faher(lca)}--\)

這樣就達到了標記我們路徑上的點的要求! 厲不厲害 (o?▽?)o tql!!

這樣點的差分應該沒什麽問題了吧 ,有問題可以問我的哦 qwq (如果我會的話.)

2.邊的差分

既然我們已經get到了點的差分,那麽我們邊的差分也是很簡單啦!

機房某dalao:"這不和點差分標記方式一樣嗎?不就是把邊塞給點嗎? 看我切了它!"

為這位大佬默哀一下 qwq.

的確,我們對邊進行差分需要把邊塞給點,但是,這裏的標記並不是同點差分一樣.

PS: 把邊塞給點的話,是塞給這條邊所連的深度較深的節點. (即塞給兒子節點

先請大家思考\(5s\)

\(\vdots\)

\(\vdots\)

\(\vdots\)

好,時間到,有沒有想到如何標記?(只要畫圖模擬一下就可以啦! 上圖!

紅色邊為需要經過的邊,綠色的數字代表經過次數

正常的話,我們的圖是這樣的.↓

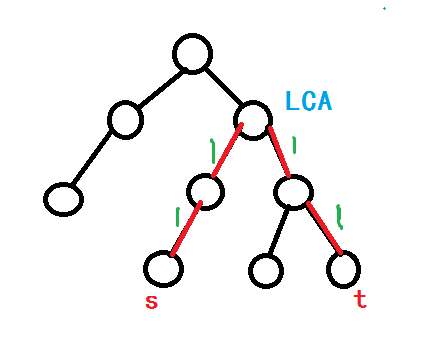
但是由於我們把邊塞給了點,因此我們的圖應該是這樣的↓

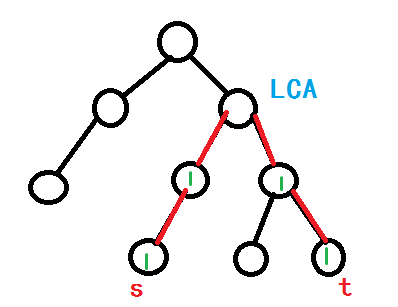
但是根據我們點差分的標記方式來看的話顯然是行不通的,

這樣的話我們會經過\(father_{LCA}--> LCA\)這一路徑.

因此考慮如何標記我們的點,來達到經過紅色邊的情況

聰明的你一定想到了,這樣來標記

\(cnt_s++\) ， \(cnt_t ++\) ，\(cnt_{LCA}-=2\)

這樣回溯的話,我們即可只經過圖中紅色邊啦!(這裏就不詳細解釋啦,原理其實相同 qwq

把邊塞入點中的代碼這樣寫.qwq(順便在搜索的時候處理即可

void dfs(int u,int fa,int dis)
{
    //u為當前節點,fa為當前節點的父親節點,dis為從fa通向u的邊的邊權.
    depth[u]=depth[fa]+1;
    f[u][0]=fa;//相信寫過倍增LCA的人都能看懂.
    init[u]=dis;//這裏是將邊權賦給點.
    for(int i=1;(1<<i)<=depth[u];i++)f[u][i]=f[f[u][i-1]][i-1];//預處理倍增數組.
    for(int i=head[u];i;i=edge[i].u)
    {
        if(edge[i].v==fa)continue;
        dfs(edge[i].v,u,edge[i].w);
    }
    //這個每個人的寫法不一樣吧.
    //所以根據每個人的代碼風格不一樣,碼出來的也不一樣
}

例題選講

代碼會在下面統一發 qwq

1. 先來一個簡單題練練手 --->p3128 最大流
   這個題應該算是樹上差分的入門題
   就是入門題qwq

   題意簡單概括一下
   求被經過次數最多的點,(其實概括出來的話,這題就裸了.)

   顯然,裸的點差分.

   所以請在課下切掉它qwq.

2. 再來一個簡單題練手 --->p3258 松鼠的新家

   也是一個簡單的樹上差分的題.不過有一些小坑點.

   讀完題大家先思考\(5s\)

   \(\vdots\)

   時間到。

   簡單分析
   很明顯,這是一道點差分.但是不同的是,我們需要在每個位置”中轉“一下.

   即從 \(a_1-->a_2\) ，\(a_2-->a_3\) ，\(a_3-->a_4\) \(\dots\)我們會重復經過\(a_2\)，\(a_3\)，\(\dots\)這一些點.

   因此我們經過這些節點次數會被重復計算,因此,我們需要將其\(--\)

   還要註意的是,當我們到達\(a_n\)這一位置的時候,小熊會吃飯 qwq ,即在這裏不會有糖果吃. 所以這個位置的經過次數也需要\(--\).

   代碼中需要註意的位置也只有這裏 這樣↓

    for(RI i=2;i<=n;i++)cnt[a[i]]--;

   3.上點難度了 ----->p2680 運輸計劃

   (可能是因為我太弱了 qwq

   先感謝dalao的講解 @GMPotlc

   讀完題,我們發現,這是一道邊差分的題.

   簡單分析
   於是建完邊我們先dfs一遍預處理出根節點到每個節點的距離.並把邊權塞給點。

   預處理距離的話只需要再在dfs中加入一句即可

   Dis[edge[i].v]=Dis[u]+edge[i].w;

   然後我們可以計算出每條航道間的距離,類似這樣

   //\(query[i].dis\)代表第i個詢問兩航道之間的距離

   //則\(query[i].dis=Dis[x]+Dis[y]-2*Dis[lca_{x,y}]\)

   不能理解這個計算的話來看圖 qwq.

   圖中給出的邊均為從根節點到達某節點的距離.

   顏色對應

   

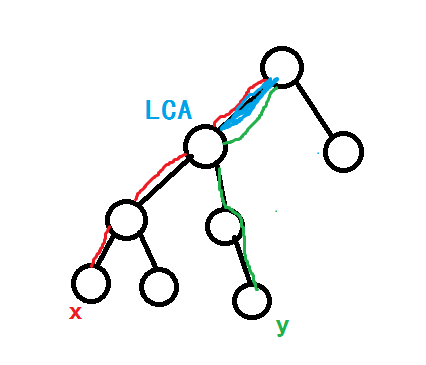
   我們發現,實際只要記錄的距離僅為LCA下面的紅色和綠色路徑.

   而我們重復經過了LCA上面的邊兩次."這沒用啊"

   因此只要減去2*Dis_{LCA}即可.

   考慮：

   我們需要將被經過次數最多,且邊權最大的邊刪去.

   這樣能使我們所用總時間最大值盡可能小 (很明顯 qwq

   要求最大值最小? 很明顯,我們想到了二分答案.

   解決

   既然想到了二分答案,那我們就二分這些路徑的長度.(即工作時間.

   如果一些路徑長度大於當前二分的mid,我們就需要記錄這些路徑上的邊其被經過次數.

   (比mid小的路徑一定已經合法,我們可以在mid時間內完成任務.)

   假設路徑長度大於mid的有num個

   (我們找到被這些路徑共同經過的最大的邊權,刪去它,使得這些路徑長度都小於mid,那麽這個mid就是合法的.

   小細節:我們可以通過排序得到最大的路徑長度,如果這條最長的路徑減去被經過次數<=mid,那這個mid就是合法的,我們就可以去尋找更優解.

   這裏引用題解裏的一句話

   因為要求求最小時間, 然而可以根據單調性可以通過二分一個時間來判定這個時間能不能成立.
   也就是通過二分答案將一個求答案的問題轉化為\(log_{2}t_{\max}\)個判定性問題.

   因此這個題就很簡單了

   PS:記得每次將標記數組清零.(因為大於mid的路徑長度會變化.

   (可能做法常數有些大,但是是可以過的.

   (也可能是評測機看臉.第一次交T了一個點,第二次交就A掉了 qwq.

上面三個題的代碼都在這裏

小結

樹上差分的裸題還是比較少的(其實是我遇到的比較少吧 qwq.

因此樹上差分與其他算法的結合考察還是比較多的

例如剛剛講的運輸計劃就是一個 LCA+樹上差分+二分.

(其實樹上差分問題一定有LCA的 qwq)

BB in last

總的來說,差分數組重點在於思想的運用.

而樹上差分一般不會直接考裸題.

所以,我們需要掌握更多的算法. qwq

不會的可以問我 ,直到今年Noip我一直會在.

如果拿到省一的話,我會待的更久,拿不到就滾回去學文化課了 qwq

差分數組 and 樹上差分