python

賦值操作和淺拷貝

佔位符，後面補充。

numpy

訪問陣列：索引和切片

如果訪問的時候使用了整數索引，那麼產生的結果的維度數會降低，如果全部使用切片，則維度數不變。

# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])

col_r1 = a[:, 1] #有一個維度是索引
col_r2 = a[:, 1:2] #都是切片
print(col_r1, col_r1.shape)  # Prints "[ 2  6 10] (3,)"
print(col_r2, col_r2.shape)  # Prints "[[ 2]
                                            #          [ 6]
                                            #          [10]] (3, 1)"
 

另外，下面兩種訪問方式等價：

print(a[[0, 1, 2], [0, 1, 0]])  # Prints "[1 4 5]"
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))  # Prints "[1 4 5]"

布林陣列訪問

a = np.array([[1,2], [3, 4], [5, 6]])
bool_idx = (a > 2)  
print(bool_idx)      # Prints "[[False False]
                            #          [ True  True]
                            #          [ True  True]]"

print(a[bool_idx]) # Prints "[3 4 5 6]"，等價於print(a[a>2])
 

按某個維度求和

先解釋一下numpy的維度。維度為(4,)，表示一維向量。維度為(4,1)，表示第一個維度有4個元素，每個元素包含一個維度為1非元素。維度為(1,4)，表示第一個維度包含1個元素，這個元素是一個維度為(4,)的向量。

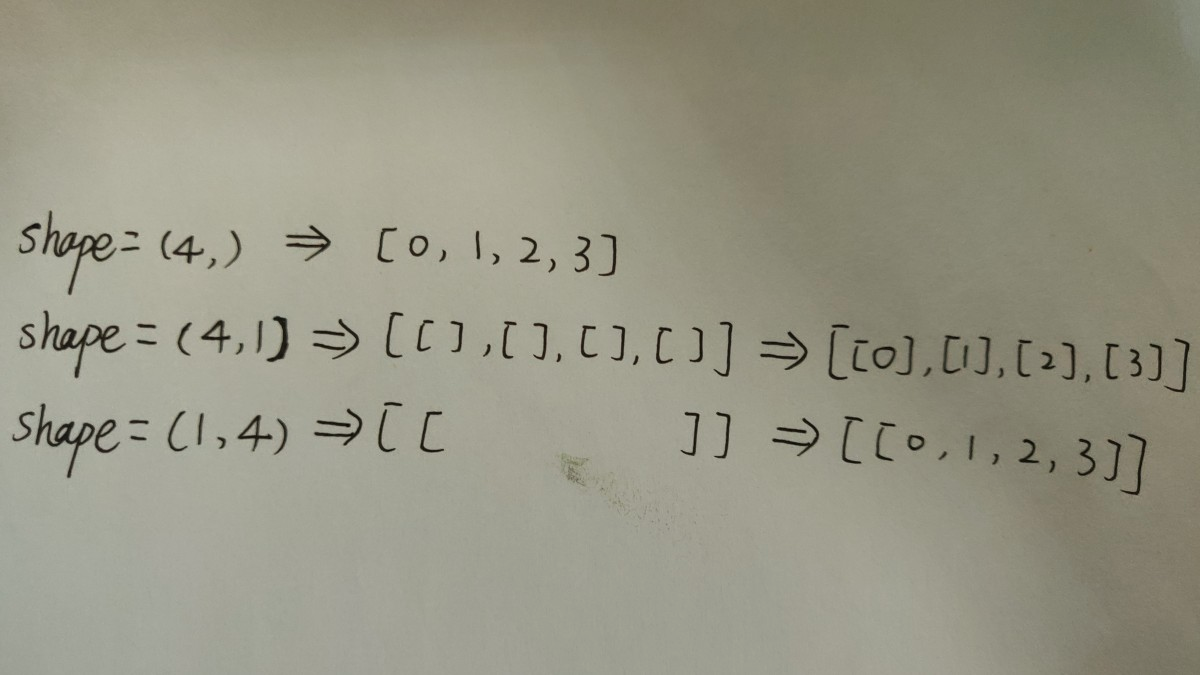
舉例說明：

# array([[1, 2, 3],
#        [4, 5, 6]])
x = np.array([[1,2,3],[4,5,6]])

x的維度是(2,3)。numpy矩陣是一種分層套的結構，第一層包含兩個元素：[1,2,3]和[4,5,6]，而這兩個元素又各自包含3個元素1,2,3和4,5,6，所以它的維度是(2,3)。注意，(2,3)和(2,3,1)是不一樣的，後者說明套了3層，寫法應該是：

y = np.array([[[1], [2], [3]], [[4], [5], [6]]])

上面y的第一層包含2個元素：[[1], [2], [3]]和[[4], [5], [6]]；這2個元素又各自包含了3個元素：[[1], [2], [3]]包含了[1], [2], [3]，[[4], [5], [6]]包含了[4], [5], [6]；它們又各自包含了1個元素，如[1]包含1，[2]包含2等。

np.sum(x)  # 計算所有元素的和，21

np.sum(x, axis=0) 
# 第一個維度內的元素求和。第一層包含2個元素：[1,2,3]和[4,5,6]，二則相加，得到[5,7,9]，shape為(3,)

np.sum(x, axis=1) 
# 第二個維度內的元素求和。首先[1,2,3]內所有元素相加，得到6，然後[4,5,6]內所有元素相加，得到15，所以結果為[6,15]，shape為(2,)

np.sum(y, axis = 0)
# 第一個維度內的元素求和，即[[1], [2], [3]]+[[4], [5], [6]]，等於[[5], [7], [9]]，shape為(3,1)

對一位陣列做轉置，相當於啥也沒幹

v = np.array([1,2,3])
print(v)    # Prints "[1 2 3]"
print(v.T)  # Prints "[1 2 3]"

廣播broadcast

廣播的原理
原理是在較低的維度上做一個repeat，然後再做element-wise的加減乘除。例如x.shape=(4,3)，y.shape=(3,)，那麼就在第一個維度上把y重複4次，得到一個shape=(4,3)的矩陣之後，再和x做element-wise運算。借用某個教程上的例子，解釋如下：

import numpy as np

# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
vv = np.tile(v, (4, 1))  # Stack 4 copies of v on top of each other
print vv                 # Prints "[[1 0 1]
                         #          [1 0 1]
                         #          [1 0 1]
                         #          [1 0 1]]"
y = x + vv  # Add x and vv elementwise
print y  # Prints "[[ 2  2  4
         #          [ 5  5  7]
         #          [ 8  8 10]
         #          [11 11 13]]"

廣播的原則
不是任意兩個矩陣或者向量都能進行廣播的，需要滿足一定的規則。兩個矩陣或向量的維度，從最後一個維度開始比較，需要滿足下面兩點之一：

• 1、某個維度上數字相等
• 2、其中一個維度等於1

下面的矩陣都是滿足要求的：

A      (2d array):  5 x 4
B      (1d array):      1
Result (2d array):  5 x 4

A      (2d array):  5 x 4
B      (1d array):      4
Result (2d array):  5 x 4

A      (3d array):  15 x 3 x 5
B      (3d array):  15 x 1 x 5
Result (3d array):  15 x 3 x 5

A      (3d array):  15 x 3 x 5
B      (2d array):       3 x 5
Result (3d array):  15 x 3 x 5

A      (3d array):  15 x 3 x 5
B      (2d array):       3 x 1
Result (3d array):  15 x 3 x 5

下面的則不滿足要求：

A      (1d array):  3
B      (1d array):  4 # trailing dimensions do not match

A      (2d array):      2 x 1
B      (3d array):  8 x 4 x 3 # second from last dimensions mismatched

SciPy

SciPy給予numpy，在此基礎上封裝了很多函式和模組。

影象處理

from scipy.misc import imread, imsave, imresize

img = imread('assets/cat.jpg')
print img.dtype, img.shape  # Prints "uint8 (400, 248, 3)"

img_tinted = img * [1, 0.95, 0.9]

# Resize the tinted image to be 300 by 300 pixels.
img_tinted = imresize(img_tinted, (300, 300))

# Write the tinted image back to disk
imsave('assets/cat_tinted.jpg', img_tinted)

matlab檔案

函式scipy.io.loadmat和scipy.io.savemat能夠讓你讀和寫MATLAB檔案。