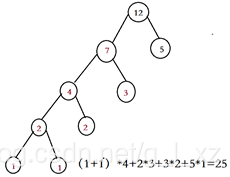
1：有以下5個葉子節點1,1,3,2,5構成的哈夫曼樹的帶權路徑長度為(D)
A：24
B：26
C：23
D：25
解析：

2：某表示式的字首形式為"±*^ABCD/E/F+GH",它的中綴形式為©
A：A^B*C-D+E/F/G+H
B：A^B*(C-D)+(E/F)/G+H
C：A^B*C-D+E/(F/(G+H))
D：A^B*(C-D)+E/(F/(G+H))
解析：
先找^AB轉換為A^B
再找*和C轉換成A^B*C
再找-和D轉換成A^B*C-D
再找+GH轉換成G+H
……
3：能在O(1)時間內訪問線性表的第i個元素的結構是（A）
A：順序表
B：單鏈表
C：單項迴圈表
D：雙向連結串列
解析

：順序表能隨機存取任意元素。
4：有n-1條邊的圖肯定都是生成樹(B)
A：對
B：錯
解析：前提是不構成迴路。
5：若已知一棵二叉樹的前序遍歷序列和後序遍歷序列，則可以恢復該二叉樹，這樣的說法正確嗎（B）
A：正確
B：不正確
解析：已知中序和前序或者中序和後序可以推出另外一種，前序和後序無法確定
6：N個結點的二叉排序樹有多種,其中樹高最小的二叉排序樹是最佳的(A)
A：對
B：錯
解析：二叉排序樹的主要用途是鏈式儲存結構的二分查詢，查詢的最壞次數是樹的高度，因此高度最小的二叉排序樹是最佳的
7：以下 C 語言指令：
int a[5] = {1,3,5,7,9};
int *p = (int *)(&a+1);
printf(“%d,%d”,*(a+1) ， *(p-1));
執行結果是什麼（C）
A：2,1
B：3,1
C：3,9
D：執行時崩潰
解析：&a表示一個指向大小為5陣列的指標，那麼(&a+1)就是表示一個指向大小為5的下一個陣列的指標, 也就是陣列a最後一個元素的下一個位置,-1則指向a中最後一個元素；a是儲存陣列的首地址，*（a+1）儲存的是陣列第二個地址的值，故為3.p是儲存陣列a最後一個位置的下一個位置的地址，*p是指向陣列a最後一個位置的下一個位置，值為-1，*（p-1）是指向陣列a最後一個位置，值為9.
8：若有說明：a[3][4];，則陣列 a 中和元素（C）
A：可在程式的執行階段得到初值 0
B：可在程式的編譯階段得到初值 0
C：陣列 a 的初值無法確定
D：可在程式的編譯或執行階段得到初值 0
解析：int a[3][4]定義了陣列但未賦初值，系統為所定義的陣列在記憶體中開闢了已連續的儲存單元，但這些儲存單元中沒有確定的值
9：以下哪些演算法是可以用來求最小生成樹（AD）
A：kruskal演算法
B：dijkstra演算法
C：floyd演算法
D：prim演算法
解析：
Kruskal演算法（適合稀疏圖，貪心演算法的運用，時間複雜度O(eloge),e為邊數）
Prim演算法適合稠密圖，貪心演算法的應用，時間複雜度為O(n+e)，臨接表儲存
B和C是求最短路徑的演算法
10：選項程式碼中能正確運算元組元素的是(AB)

int main(){
int a[N][N]={{0,0},{0,0}};
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++){
			//訪問二維陣列a的值
			//選項程式碼
		}
	}
}

A：*(*(a+i)+j)=1
B：*(a[i]+j)=1
C：**(a+i)[j]=1
D：*((a+i)+j)=1
解析：陣列名當被直接使用時，是一個指向陣列首地址的指標。如果陣列是多維陣列，那麼陣列名是指向第一行陣列的首地址，而不是第一行第一列單個元素的地址，所以*(a+i)與a[i]是一個意思，當直接用a[i]時代表的是該一維陣列的首地址，所以*(a[i]+j)是與a[i][j]等效，所以AB選項正確