1.員工的重要性

難度：簡單
給定一個儲存員工資訊的資料結構，它包含了員工唯一的id，重要度 和 直系下屬的id。

比如，員工1是員工2的領導，員工2是員工3的領導。他們相應的重要度為15, 10, 5。那麼員工1的資料結構是[1, 15, [2]]，員工2的資料結構是[2, 10, [3]]，員工3的資料結構是[3, 5, []]。注意雖然員工3也是員工1的一個下屬，但是由於並不是直系下屬，因此沒有體現在員工1的資料結構中。
現在輸入一個公司的所有員工資訊，以及單個員工id，返回這個員工和他所有下屬的重要度之和。

示例 1:
輸入: [[1, 5, [2, 3]], [2, 3, []], [3, 3, []]], 1
輸出: 11
解釋:
員工1自身的重要度是5，他有兩個直系下屬2和3，而且2和3的重要度均為3。因此員工1的總重要度是 5 + 3 + 3 = 11。

注意:
一個員工最多有一個直系領導，但是可以有多個直系下屬
員工數量不超過2000。

思路：很明顯，該題用深度優先搜尋可以解決，即員工的重要性取決於他本身和下屬員工的重要性，那麼只需要知道下屬員工的重要度即可，利用遞迴很容易求解。

/*
// Employee info
class Employee {
public:
    // It's the unique ID of each node.
    // unique id of this employee
    int id;
    // the importance value of this employee
    int importance;
    // the id of direct subordinates
    vector<int> subordinates;
};
*/
class Solution {
public:
    int getImportance(vector<Employee*> employees, int id) {
           int totalDegree=0;
           totalDegree=getImpDegree(employees,id,totalDegree);
           return totalDegree;
    }
     int getImpDegree(vector<Employee*> employees,int id,int &totalDegree){
             Employee* targetEmployee;
             for(int j=0;j<employees.size();j++){
                 if(employees[j]->id==id){      //從容器中搜索對應id的Employee的陣列
                     targetEmployee=employees[j];
                 }
             }
             totalDegree+=targetEmployee->importance;
             if(targetEmployee->subordinates.size()==0) return targetEmployee->importance; //遞迴的邊界條件
             for(int i=0;i<targetEmployee->subordinates.size();i++){
                  int impDegree=getImpDegree(employees,targetEmployee->subordinates[i],totalDegree); //依次得到下屬員工的重要度
         }
         return totalDegree;
     }
};
 

2. N叉樹的最大深度

難度：簡單

給定一個 N 叉樹，找到其最大深度。
最大深度是指從根節點到最遠葉子節點的最長路徑上的節點總數。
例如，給定一個 3叉樹 :

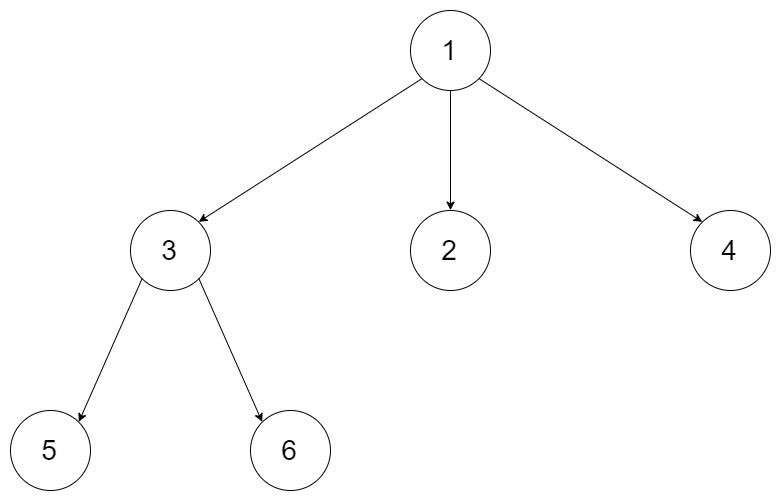
說明:

樹的深度不會超過 1000。
樹的節點總不會超過 5000。

思路：其實該題跟獲得二叉樹的最大深度類似，用遞迴實現深度優先搜尋，注意邊界條件。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/
class Solution {
public:
    int maxDepth(Node* root) {
        if(root==NULL) return 0;
        int maxDepth=getMaxDepth(root);
        return maxDepth;
    }
    int getMaxDepth(Node* root){
        if(root->children.size()==0) {return 1;}
        int MaxDepth=0;
        for(int i=0;i<root->children.size();i++){
            int tempDepth=getMaxDepth(root->children[i]);
            if(MaxDepth<tempDepth+1){
                MaxDepth=tempDepth+1;
            }
        }
        return MaxDepth;
    }
};
 

3. 葉子相似的樹

難度：簡單
請考慮一顆二叉樹上所有的葉子，這些葉子的值按從左到右的順序排列形成一個 葉值序列 。

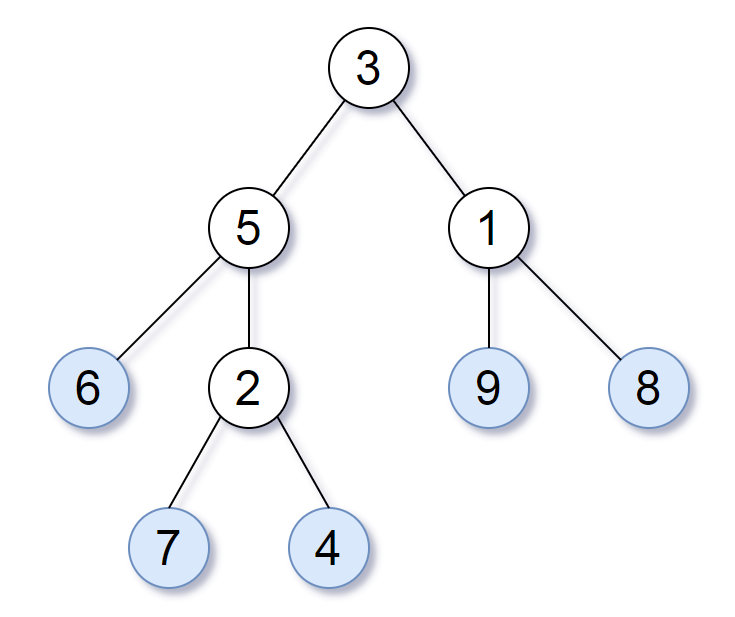
舉個例子，如上圖所示，給定一顆葉值序列為 (6, 7, 4, 9, 8) 的樹。
如果有兩顆二叉樹的葉值序列是相同，那麼我們就認為它們是 葉相似 的。
如果給定的兩個頭結點分別為 root1 和 root2 的樹是葉相似的，則返回 true；否則返回 false 。

提示：
給定的兩顆樹可能會有 1 到 100 個結點。

思路：用倆個容器儲存倆顆樹中的葉子值，然後對比倆個容器是否相等即可，該題主要考深度優先搜尋和樹。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool leafSimilar(TreeNode* root1, TreeNode* root2) {
        vector<int> root1Leaf=getLeaf(root1);
        vector<int> root2Leaf=getLeaf(root2);
        return root1Leaf==root2Leaf;
    }
    vector<int> getLeaf(TreeNode* root){
        vector<int> allLeaf;
        stack<TreeNode*> stack;
        while(root!=NULL || !stack.empty()){
            while(root){
                stack.push(root);
                if(root->left==NULL && root->right==NULL){
                    allLeaf.push_back(root->val);
                }
                root=root->left;
            }
            if(!stack.empty()){
                root=stack.top()->right;
                stack.pop();
            }
        }
        return allLeaf;
    }
};